obiekt : Kategoria ma obiekty i morfizmy. Chociaż pojęcie obiekt jest podstawowym w teorii kategorii, obiekty mogą być rozumiane jako uogólnienie lub abstrakcyjny konkretny byt matematyczny. Poniższe kategorie są przykładami standardowymi (obiekty są wymienione na pierwszym miejscu, morfizmy na drugim): przestrzenie topologiczne i funkcje ciągłe; grupy abelowe i homomorfizmy grupy; pierścienie i homomorfizmy pierścieni; częściowo uporządkowane zbiory i funkcje monotoniczne; zespolone przestrzenie Banacha i ograniczone przekształcenia liniowe; zbiory i funkcje injektywne; zbiory i funkcje surjektywne

oblique [wypukłe] : Ani prostopadłe ani poziome

oblique angle [kąt wypukły] : kąt nie będący wielokrotnością kąta prostego

oblique cylinder [cylinder wypukły] : Cylinder, który nie jest poprawnym cylindrem

oblique triangle : Trójkąt , który nie będący trójkątem prostokątnym

obtuse angle [kąt rozwarty] : Kąt większy niz 90^o I mniejszy niż 180^o

obtuse triangle [trójkąt rozwartokątny] : Trójkąt zawierający kąt rozwarty.

octagon [osmiokąt] : Wielokąt mający osiem boków

octahedron [ośmiościan] : Wielościan z ośmioma ścianami. Regularny ośmiościan, jeden z pięciu brył platońskich , ma 8 trójkątnych ścianek, 12 brzegów i 6 wierzchołek

omits [pomijanie] : Model A teorii T pomija typ Θ jeśli i tylko jeśli nie zdaje sobie sprawy. To znaczy, A pomija Θ jeśli i tylko jeśli nie ma n-krotki a^ elementów A takich ,że A |= Φ(a^) dla każdego Φ(x^) w Θ(x^)

one [jeden] :
(1)Najmniejsza dodatnia liczba całkowita, oznaczona przez 1
(2)Tożsamość multiplikatywna liczb zespolonych (a więc liczb rzeczywistych, liczb wymiernych i liczb całkowitych). To znaczy, jeśli z jest liczba zespoloną, wtedy 1 ⋅ = z ⋅ 1 = z

one-point compactification [uzwarcenie Aleksandrowa] : Przestrzeń zwarta X_C uzyskana z danej przestrzeni topologicznej X przez przyłączenie pojedynczego punky ∞ do X. Definicja topologii na X_C wymaga ,aby X była lokalną zwartą przestrzenią Hausdorffa. Zbiory otwarte w X_C są potem definiowane aby były zbiorami otwartymi z X a dowolny zbiór postaci V ∪ {∞} gdzie V jest podzbiorem otwartym z X którego dopełnieniem jest zbiór zwarty. Zauważ, że X jest podprzestrzenią z X_C. Uzwarcenie Aleksandrowa linii rzeczywistej jest homeomorficzne do okręgu, podczas gdy uzwarcenie Aleksandrowa płaszczyzny jest homeomorficzne do kuli. Ostatni przykład jest szczególnie ważny w analizie zespolonej gdzie homeomorfizm jest nazywany rzutowaniem stereograficznym

odpowiedniość wzajemnie jednoznaczna : Dowolna funkcja, która jest wzajemnie jednoznaczna (injektywna) i onto (surjektywna); również znana jako funkcja bijektywna lub bijekcją. Na przykład, funkcja f:R → R dana przez f(x) = 3x-2 jest odpowiedniością wzajemnie jednoznaczną

one-to-one function [funkcja wzajemnie jednoznaczna] : Dowolna funkcja f:A →l B , gdzie A i B są zbiorami arbitralnymi, takimi ,że dla każdego x, y ∈ A, f(x) = f(y) implikuje x = y. Znana również jako funkcja injektywna, lub injekcją.

onto : Jeśli A i B są zbiorami arbitralnymi, dowolna funkcja f:A → B taka ,że dla każdego y ∈ B istnieje x ∈ A spełniające f(x) = y jest funckją onto. Znan równie jako funkcja surjektywną , lub jako surjekcja. Na przykład, funkcja f:R → R daną przez f(x) = x³ jest onto

otwarta kula : W przestrzeni metrycznej X, dowolny zbiór postaci B = {y:d(x,y) < r}, z pewnym środkiem x ∈ X i promieniem r > 0. W przestrzeni metrycznej, zbiór otwartych kul formuje bazę dla topologii metrycznej. Na przykład ,w R³ ze zwykłym metryczny dystansem, otwarte kule są tylko wewnętrznymi sferami

open cover [pokrycie otwarte] : Pokrycie otwarte podprzestrzeni A przestrzeni topologicznej X jest zbiorem {U_α, otwartego podzbioru X takim ,że suma wszystkich U_α zawiera A .Otwarte pokrycia obejmuje definicję zwartości.

otwarty dysk : Otwarta kula w R² ze zwykłąś metryką dystansu. To znaczy, D jest dyskiem otwartym ze środkiem x = (x₁, x₂) ∈ R² i promieniu r > 0 jeśli

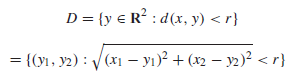
otwarta formuła : Formuła α języka pierwszego rzędu L takiego ,że α jest wolnym kwantyfikatorem tj. α nie ma żadnego kwantyfikatora

otwarte przekształcenie : Funkcja f:X → Y taka ,że obraz f(U) otwartego zbioru U z X jest zbiorem otwartym w Y. Jeśli f jest odwracana, wtedy f jest przekształceniem otwartym jeśli i tylko jeśli f^-1 : Y → X jest ciągła.

owtarta n-kula : Otwarta kula w Rⁿ ze zwykłą metryką odległości. To znaczy, B jest otwartą w n-kulą ze środkiem
x = (x₁, x₂,…,x_n) ∈ Rⁿ
i promieniem r > 0 jeśli
B = {y ∈ Rⁿ : d(x,y) < r},
gdzie

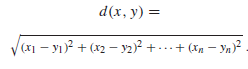
otwarty zbiór : Podzbiór U przestrzeni topologicznej X która należy do topologii na X

owtarty sympleks : Wnętrze Int(σ) sympleksu σ .Szczególnie , Int(σ) = σ\Bd(σ) gdzie Bd(σ) , ograniczenie σ jest sumą wszystkich właściwych ścian σ. Na przykład, otwarty 1- sympleks jest otwartym przedziałem, podczas gdy otwarty 2-sympleks jest wnętrzem trójkąta.

otwarta gwiazda : Jeśli S jest kompleksem symplycjalnym i v jest wierzchołkiem z S, otwarta gwiazda wierzchołka v jest określona przez sumę wnętrz wszystkich symplicjałów σ z S , które mają v jako wierzchołek.

opposite angle [kąt przeciwległy] : Dwa kąty wielokąta (mający parzystą liczbę boków) o takiej samej liczbie kątów między nimi, niezależnie od kierunku według którego jeden zlicza

opposite angle/side [kąt / bok przeciwległy] : Strona I kąt w wielokącie (o nieparzystej liczbie stron) mająca równą liczbę stron między nimi, bez względu na kierunek według którego zliczamy

opposite side [przeciwległy bok] : Para boków wieloboka (mającego parzystą liczbę boków) mająca równą liczbę boków między nimi ,bez względu na kierunek wokół którego zlczamy.

ordered n-tuple [porządek n-krotny] : Lista n dowolnych obiektów z określonym porządkiem, widocznych jako pojedynczy obiekt. Pierwszy element n-krotności jest obiektem wyświetlonym najpierw, n-ta składowa jest obiektem wyświetlanym jako ostatnim

ordered pair [para uporządkowana] : Uporządkowana lista dwóch obiektów. Pierwszy (drugi) element pary uporządkowanej jest obiektem wyświetlanym pierwszym (drugim). Na przykład, (-1,A), jest parą uporządkowaną z -1 i A jako pierwszym i drugim elementem, odpowiednio

ordered triple [uporządkowana trójka] : Uporządkowana n-krotka z n = 3

ordering [uporządkowanie] : Częściowe uporządkowanie (na zbiorze A)

order topology [topologia porządkowa] : Topologia na zbiorze X, z relacją porządku liniowego, z bazą składającą się ze wszystkich przedziałów postaci (a,b) dla dowolnego a,b ∈ X. Jeśli X ma albo element minimalny m lub element maksymalny M, wtedy zbiory [m,b) i (a,M] są również dołączane. Topologia porządkowa jest topologią standardową; to znaczy, topologią z bazą składającą się z otwartych przedziałów

order type (of a well-ordered set) [typ porządkowy zbioru dobrze uporządkowanego] : Unikalna liczba porządkowa, która jest uporządkowana izomorficznie do danego dobrze uporządkowanego zbioru .Zatem zbiór {-2,1,5} który jest dobrze uporządkowany prze relację -2 < 1 < 5 ma typ porządkowy 3. Zbiór N ∪{#}, który jest dobrze uporządkowany przez relację 0 < 1 < 2 < 3 < … < #, ma typ porządkowy ω + 1

odrinal (ordinal numer) [liczba porządkowa] : Zbiór tranzytywny , który jest ściśle dobrze uporządkowany przez element relacji ∈ . Na przykład, liczba porządkowa 3 jest zbiorem {0,1,2} jest zbiorem tranzytywnym i jest dobrze uporządkowany przez ∈

ordinary helix [zwykła linia śrubowa] : Krzywa leżąca na cylindrze ,która formuje stały kąt z elementami tego cylindra.

ordinate [rzędna] : Współrzędna y punktu na płaszyźnie kartezjańskiej xy jest rzędną tego punktu. Na przykład rzędna punktu (2 ,-3) jest -3.

orientowalna wiązka włókna : Wiązka włókna F → E → B, z F spójną, zwartą n-rozmaitością, taką,że jest możliwe wybranie elementu w homologii H_n(F_b z włókna powyżej każdego punktu b w B tak więc wokół każdego punktu jest otoczenie U i generator homologii H_n(E|_U) z E ograniczony do U tak więc inkluzja włókna do E|_U indukuje przekształcenie , które pobiera (wybiera) generator z H_n(F_b) do (wybrania) generatora z H_n(E|sub>U.

orientacja : Określa wybór kierunku dla przestrzeni wektorwej, sympleksu lub komórki. Definicja orientacji dla tych obiektów rozciąga się na ważne pojęcia orientacji na rozmaitość, kompleks symplicjalny lub komórkę zespoloną
(1)Dla n-wymiarowej przestrzeni wektorowej V, orientacja jest określona przez wybór uporządkowanej podstawy {v₁,…,v_n}. Druga podstawa {w₁,…,w_n} daje tą samą orientację dokładnie kiedy wyznacznik wybranej podstawy macierze z {v₁,…,v_n} do {w₁,…,w_n}jest dodatni. Na przykład, uporządkowana podstawa {(1,0,0),(0,1,0),(0,0,1)} daje orientację z R³ znaną jako orientacja prawostronna
(2)Orientacja sympleksu jest określona porządkiem jego wierzchołków; dwa uporządkowane są równoważne jeśli jeden jest parzystą permutacją drugiego.
(3)Orientacja komórki e_n (homeormoficzna do n-wymairowej kuli) jest wybraniem generatora dla względnej grupy homologii nieskończenie cyklicznej. H_n(e_n,Bd(e_n)
(4)Przy danej rozmaitości M, każdy punkt jest zawarty w otwartym zbiorze, który jest homeomorficzny do Rⁿ. Zatem, używając definicji orientacji dla przestrzeni wektorowej, M może być pokryte przez zbiory otwarte takie ,że każdy otwarty zbiór ma orientację. Jeśli dwa takie zbiory otwarte U i V nie są rozłączne, możemy spytać czy orientacja na U ∩ V dziedzicząca z U jest taka sama lub przeciwna do tej dziedziczonej z V. Jeśli orientacja na U ∩ V jest taka sama, mówimy ,że U i V są zorientowane spójnie. Orientacja rozmaitości M jest definiowana przez wybór spójnie zorientowanych zbiorów otwartych , które pokrywają M.
(5)Podobnie, w kompleksie symplycjalnym lun komórkowym, każdy punkt jest zawarty w sympleksie lub komórce, które mogą mieć orientcję. Orientacja kompleksu jest spójnym wyborem orientacji dla każdej komórki lub sympleksu. Zauważ ,że jeśli rozmaitość lub kompleks mogą być zorientowane, wtedy mogą mieć odwróconą orientację. Wiele rozmaitości i kompleksów nie może być zorientowanych. Na przykład otwarta wstęga Möbiusa nie może być zorientowana

orientacja zachowania odwzorowania : Dowolne przekształcenie między zorientowanymi wiązkami lub zorientowanym rozmaitościami które odwzorowują orientację domeny do orientacji kodomeny. (ponieważ homologia jest naturalna, przekształcenie między rozmaitościami indukuje przekształcenie od homologii jednej wiązki lub rozmaitości do drugiej)

orientacja odwróconego przekształcenia. : Dowolne przekształcenie między zorientowanym wiązkami lub zorientowanymi rozmaitościami, które przekształca zorientowaną domenę do ujemnie zorientowanej kodomeny

oriented copmplex [zorientowany complex] : Kompleks symplicjalny lub komórkowy z orientacją

orthocenter [ortocentrum] : Punkt przecięcia trzech wysokości trójkąta

ortogonalny : Pod kątem prostym

orthogonal complement [dopełnienie ortogonalne] : Dana podprzestrzeń W przestrzeni wektorowej V, jednoznaczna podprzestrzeń U z V taka ,że V = U ⊕ W i każdy wektor w U jest prostopadły do każdego wektora w W

ortogonalny system współrzędnych : System współrzędnych w którym kiedy i ≠ j
, wektor z 1 na i-tej pozycji i zera w każdej innej jest ortogonalny do wektora z 1 w j-tej pozycji i zer w każdej innej.

ortogonalna ramka : W geometrii różniczkowej zbiór uporządkowany (x,v₁,…v_n) składający się z punktu x i ortonormalnych wektorów v₁,…,v_n

ortogonalna grupa : Grupa wszystkich n x n ortogonalnych macierzy pod mnożenie .Macierz ortogonalna jest macierzą , której odwrotność jest równa jej traznpozycji

ortogonalny rzut : Liniowa transformacja T:V → V z przestrzeni iloczynu skalarnego V do samej siebie tak ,że T = T² = T^*, gdzie T^* oznacza sprzężenie z T.

ortogonalna transformacja : Transformacja liniowa której macierz A jest macierzą ortogonalną tj. A^-1 = A^t

ortogonalne wektory : Zbiór wektorów , które są ortogonalnie parowe

ortonormalne : Zbiór wektorów ,które są ortogonalne i mają wartość bezwględną 1.

ortonormalizacja Proces w którym zbiór niezależnych wektorów może być przekształcony na zbiór ortonormalny o równym rozmiarze podczas obejmowaniu tej samej przestrzeni

osculating circle [koło krzywizny] : Biorąc pod uwagę punkcie P na krzywej, koło, kóre jest ograniczone (jeśli to istnieje) jeśli punkt Q pdochodzi do P wzdłuż krzywej koła przechodzącej przez Q i styczną do C w punkcie P.

owal : Dowolna krzywa jajowata. Ogólnie, ograniczenie ciała wypukłego w R²

owaloid ograniczenie ciała wypukłego w R³