
Księga Mathmy Tom I
Księga Mathmy Tom II

Mrówki są owadami społecznymi, które wyewoluowały z os w okresie środkowej kredy, około 150 milionów lat temu. Po wzroście roślin kwiatowych, około 100 milionów lat temu, mrówki zróżnicowały się w liczne gatunki. Mrówka z pustyni Saharan, Cataglyphis fortis, pokonuje ogromne odległości przez piaszczyste tereny, często całkowicie pozbawione równości gdy szuka żywności. Stworzenia te mogą wrócić do swojego gniazda przy użyciu bezpośredniej trasy, zamiast odtwarzać ścieżkę wychodzącą. Nie tylko oceniają kierunki, używając światła z nieba do orientacji, ale także wydają się mieć wbudowany "komputer", który działa jak krokomierz, który liczy ich kroki i pozwala im mierzyć dokładne odległości. Mrówka może przemieścić się do około 50 metrów, dopóki nie napotka martwego owada, po czym rozrywa kawałek, przenosząc go bezpośrednio z powrotem do gniazda, dostępnego przez otwór o średnicy często mniejszej niż milimetr. Poprzez manipulowanie długościami nóg mrówek, aby dać im dłuższe i krótsze kroki, zespół badawczy niemieckich i szwajcarskich naukowców odkrył, że mrówki "liczą" kroki, aby ocenić odległość. Na przykład po osiągnięciu celu mrówki wydłużono nogi, dodając szczudła lub skracając przez częściową amputację. Badacze zawrócili następnie mrówki, aby mrówki mogły rozpocząć podróż powrotną do gniazda. Mrówki ze szczudłami posuwały się zbyt daleko i mijały wejście do gniazda, podczas gdy te z amputowanymi nogami nie osiągały go. Jednakże, jeśli mrówki rozpoczęły swoją podróż od gniazda ze zmodyfikowanymi nogami, były w stanie obliczyć odpowiednie odległości. Sugeruje to, że decydującym czynnikiem jest długość kroku. Co więcej. wysoce wyrafinowany komputer w mózgu mrówki umożliwia mrówce obliczenie ilości związanej z poziomym rzutem swojej drogi, tak aby nie zagubiła się nawet wtedy, gdy piaszczysty pejzaż rozwija wzgórza i doliny podczas swojej podróży.
Około 60 milionów lat temu małe, podobne do lemurów naczelne wyewoluowały w wielu rejonach świata, a 30 milionów lat temu istniały naczelne o cechach przypominających małpy. Czy takie stworzenia mogą liczyć? Znaczenie liczenia zwierząt jest bardzo sporną kwestią wśród ekspertów od zachowań zwierząt. Jednak wielu badaczy sugeruje, że zwierzęta mają pewne poczucie liczby. H. Kalmus pisze w swoim artykule "Zwierzęta jako matematycy": Nie ma teraz wątpliwości, że niektóre zwierzęta, takie jak wiewiórki czy papugi, mogą być szkolone do liczenia. ... W przypadku wiewiórek, szczurów i owadów zapylających odnotowano przypadki zliczeń. Niektóre z tych zwierząt i inne mogą odróżnić liczby w podobnych wzorach wizualnych, podczas gdy inne mogą być przeszkolone w rozpoznawaniu, a nawet reprodukcji sekwencji sygnałów akustycznych. Kilku z nich można nawet wytrenować, aby wyciągnąć liczby elementów (kropek) we wzorcu wizualnym ... Brak wymawianej liczby i napisany symbol sprawia, że wielu ludzi niechętnie przyjmuje zwierzęta jako matematyków. Wykazano, że szczury "zliczają", wykonując czynności odpowiednią liczbę razy w zamian za nagrodę. Szympansy mogą naciskać cyfry na komputerze, które pasują do liczby bananów w pudełku. Testsuro Matsuzawa z Instytutu Badań nad Prymatem na Uniwersytecie w Kioto w Japonii nauczył szympansa rozpoznawać numery od 1 do 6, naciskając odpowiedni klawisz komputera, gdy pokazano mu określoną liczbę obiektów na ekranie komputera. Michael Beran, naukowiec z Georgia State University w Atlancie w stanie Georgia, wyszkolił szympansy do korzystania z ekranu komputera i joysticka. Ekran wyświetlił cyfrę, a następnie serię kropek. a szympansy musiały pasować do dwóch. Jeden szympans nauczył się cyfr od I do 7, a inny zdołał policzyć do 6. Gdy szympansy były testowane ponownie po przerwie trzech lat, oba szympansy były w stanie dopasować liczby, ale z podwójnym poziomem błędu.
Cykady to uskrzydlone owady, które wyewoluowały około 1,8 miliona lat temu w epoce plejstocenu, kiedy lodowce posuwały się i wycofywały w Ameryce Północnej. Cykady z rodzaju Magicicada spędzają większość życia pod ziemią, żywiąc się sokami korzeni roślin, a następnie wyłaniają się, kojarzą i umierają szybko. Stworzenia te wykazują zaskakujące zachowanie: Ich pojawianie się jest zsynchronizowany z okresami lat, które są zwykle pierwszymi liczbami 13 i 17. (Liczba pierwsza jest liczbą całkowitą, taką jak 11, 13 i 17, która ma tylko dwa dzielniki całkowite: 1 i samą siebie. Wiosną 13 lub 17 roku, te okresowe cykady budują tunel wylotowy. Czasami więcej niż 1,5 milionów osobników pojawia się w jednym akrze; ta obfitość ciał może mieć wartość przetrwania, ponieważ przytłacza drapieżniki, takie jak ptaki, które nie mogą ich zjeść na raz. Niektórzy badacze spekulowali, że nastąpiła ewolucja cykli pierwszorzędowych, tak że stworzenia zwiększyły swoje szanse na uniknięcie krótszych żyjących drapieżników i pasożytów. Na przykład, jeśli cykady te mają 12-letni cykl życia, wszystkie drapieżniki z cyklami życia wynoszącymi 2, 3, 4 lub 6 lat mogą łatwiej znaleźć owady. Mario Markus z Instytutu Fizjologii Molekularnej im. Maxa Plancka w Dortmundzie w Niemczech i jego współpracownicy odkryli, że tego rodzaju cykle liczb pierwszych powstają naturalnie z ewolucyjnych matematycznych modeli interakcji między drapieżnikiem a ofiarą. Aby eksperymentować, najpierw przypisali losowe czasy trwania cyklu życia do symulowanych przez komputer populacji. Po pewnym czasie sekwencja mutacji zawsze blokowała syntetyczne cykady w stabilnym cyklu liczby pierwszej. Oczywiście badania te wciąż są w powijakach i wiele pytań pozostaje. Co jest specjalnego w 13 i 17? Jakie drapieżniki lub pasożyty faktycznie istniały, aby sterować cykadami w tych okresach? Tajemnicą pozostaje również, dlaczego spośród 1500 gatunków cykady na całym świecie tylko niewielka liczba rodzaju Magicicada jest okresowa.
Wykorzystanie węzłów może poprzedzać współczesnego człowieka (Homo sapiens). Na przykład muszle w kolorze ochry, przebite dziurami i datowane na 82 000 lat temu odkryto w jaskini marokańskiej. Inne dowody archeologiczne sugerują znacznie starsze stosowanie muszli u ludzi. Przebicie oznacza użycie sznurków i użycie węzła do przytrzymania przedmiotów w pętli, na przykład naszyjnika. Kwintesencją ozdobnych węzłów jest Księga Kellsa, bogato ilustrowana Biblia ewangelizacyjna, stworzona przez celtyckich mnichów ok. 800 r. n.e. W czasach współczesnych badanie węzłów, takich jak węzeł koniczyny z trzema skrzyżowaniami, jest częścią wielkiej gałęzi matematyki zajmująca się zamkniętymi skręconymi pętlami. W 1914 r. Niemiecki matematyk Max Dehn (1878-1952) wykazał, że lustrzane odbicie węzłów koniczyny nie jest równoważne. Przez wieki matematycy próbowali wypracować sposoby rozróżniania splotów, które wyglądają jak węzły (zwane rozsupłanym) od prawdziwych węzłów i odróżniania prawdziwych węzłów od siebie. Z biegiem lat matematycy stworzyli pozornie niekończące się tabele wyraźnych węzłów. Jak dotąd zidentyfikowano ponad 1,7 miliona nierównomiernych węzłów ze zdjęciami zawierającymi 16 lub mniej skrzyżowań. Całe konferencje są dziś poświęcone węzłom. Naukowcy badają węzły na polach, począwszy od genetyki molekularnej, aby pomóc nam zrozumieć, w jaki sposób rozplątać pętlę DNA na fizykę cząstek elementarnych, próbując przedstawić podstawową naturę cząstek elementarnych. Węzły były kluczowe dla rozwoju cywilizacji, tam gdzie były używane do wiązania ubrań, zabezpieczania broni przy ciele, do tworzenia schronień oraz do umożliwiania żeglugi statków i eksploracji świata. Dzisiaj , teoria węzłów w matematyce stała się tak zaawansowana, że zwykłym śmiertelnikom trudno jest zrozumieć jego najgłębsze zastosowania. W ciągu kilku tysiącleci ludzie przekształcili węzły z prostych wiązań z naszyjników w modele tkanin rzeczywistości.
W 1960 r. Belgijski geolog i odkrywca Jean de Heinzelin de Braucourt (1920-1998) odkrył kości pawiana z oznaczeniami w dzisiejszej Demokratycznej Republice Konga. Kość Ishango, z sekwencją nacięć, została po raz pierwszy uznana za prosty rabosz używany przez Afrykanów z epoki kamienia. Jednak według niektórych naukowców znaki sugerują matematyczną skuteczność, która wykracza poza liczenie przedmiotów. Kość została znaleziona w Ishango, w pobliżu górnego biegu rzeki Nilu, domu dużej populacji z górnego paleolitu przed erupcją wulkanu, która pochowała strefę. Jedna kolumna śladów na kości zaczyna się od trzech nacięć, które podwajają się do sześciu nacięć. Cztery wycięcia podwajają do ośmiu. Dziesięć nacięć jest o połowę mniejsze niż pięć. Może to sugerować proste zrozumienie podwojenia lub zmniejszenia o połowę. Jeszcze bardziej uderzający jest fakt, że liczby w innych kolumnach są nieparzyste (9, II, 13, 17, 19 i 21). Jedna kolumna zawiera liczby pierwsze między 20 a 20, a liczby w każdej kolumnie sumują się do 60 lub 48, obie wielokrotności 12. Odkryto kilka rboszy, które istniały wcześniej niż kość Ishango. Na przykład kość Swaziland Lebombo to 37 000 letnia strzałka piszczelowa pawiana z 29 nacięciami. W Czechosłowacji znaleziono 32 000-letnie piszczelowe kości wilka z 57 nacięciami, pogrupowane po pięć. Chociaż jest to dość spekulacyjne, niektórzy wysunęli hipotezę, że oznaczenia na kości Ishango stanowią rodzaj dodatkowego kalendarza dla kobiety z epoki kamienia, która śledziła cykle miesiączkowe, co dało początek sloganowi "miesiączka stworzyła matematykę". Nawet jeśli Ishango było prostym narzędziem księgowym, te liczby wydają się odróżniać nas od zwierząt i stanowią pierwsze kroki do symbolicznej matematyki. Pełna tajemnica kości Ishango nie może zostać rozwiązana, dopóki nie odkryje się innych podobnych kości.
Starożytni Inkowie używali quipusa (wymawiane "key-poos"), banków pamięci zbudowanych z łańcuchów i węzłów, do przechowywania liczb. Do niedawna najstarszy znane quipu pochodzi z około 650 r. n.e. Jednakże w 2005 r. quipu z peruwiańskiego nadmorskiego miasta Caral datowane było na około 5 000 lat temu. Inkowie z Ameryki Południowej mieli złożoną cywilizację ze wspólną religią państwową i wspólnym językiem. Chociaż nie mieli pisma, zachowywali obszerne zapisy zakodowane przez system logiczno-liczbowy na quipusie, który różnił się złożonością od trzech do około tysiąca sznurów. Niestety, kiedy Hiszpanie przybyli do Ameryki Południowej, zobaczyli dziwaczne quipu i myśleli, że to są dzieła Diabła. Hiszpanie zniszczyli ich tysiące w imię Boga, a dzisiaj pozostało ich tylko około 600. Rodzaje i pozycje, kierunki warkocza, poziomy sznurków, kolory i odstępy oznaczają liczby odwzorowane na obiekty świata rzeczywistego. Różne grupy węzłów zostały użyte dla różnych potęg 10. Węzły były prawdopodobnie używane do rejestrowania zasobów ludzkich i materialnych oraz informacji kalendarza. Quipus mógł zawierać więcej informacji, takich jak plany budowy, wzory tańca, a nawet aspekty historii Inków. Quipu jest znaczące, ponieważ rozwiewa przekonanie, że matematyka liczy się dopiero po rozwinięciu się cywilizacji; jednakże społeczeństwa mogą docierać do stanów zaawansowanych, nawet nie opracowując pisemnych zapisów. Co ciekawe, dzisiaj istnieją systemy komputerowe, których menedżery plików nazywają się quipus, na cześć tego bardzo użytecznego starożytnego urządzenia. Jednym złowieszczym zastosowaniem quipu przez Inków był kalkulator śmierci. Roczne kwoty dorosłych i dzieci które były zabijane rytualnie, a to przedsięwzięcie zostało zaplanowane przy użyciu quipu. Jakiś quipus reprezentował imperium, a sznury odnosiły się do dróg i węzłów ofiarnych ofiar.
Wyobraź sobie świat bez liczb losowych. W latach czterdziestych generowanie statystycznie losowych liczb było ważne dla fizyków symulujących wybuchy termojądrowe, a obecnie wiele sieci komputerowych wykorzystuje losowe liczby, aby pomóc w kierowaniu ruchem internetowym w celu uniknięcia przeciążenia. Ankietowani polityczni używają liczb losowych, aby wybrać bezstronne próbki potencjalnych wyborców. Kostki, pierwotnie wykonane z kostek kopytnych zwierząt, były jednym z najwcześniejszych środków do tworzenia liczb losowych. W starożytnych cywilizacjach uważano, że bogowie kontrolują wynik rzutu kostką; w ten sposób kości były uzależnione od podejmowania kluczowych decyzji, od wyboru władców do podziału majątku w spadku. Nawet dziś metafora Boga kontrolującego kości jest powszechna, o czym świadczy cytat Stephena Hawkinga: "Nie tylko gra w kości, ale czasami myli nas, rzucając nimi tam, gdzie nie można ich zobaczyć". Najstarsze znane kości zostały wykopane razem z tryktrakiem liczącym 5000 lat w legendarnym Burnt City w południowo-wschodnim Iranie. Miasto reprezentuje cztery etapy cywilizacji, które zostały zniszczone przez pożary, zanim zostały porzucone w 2100 rok p.n.e. W tym samym miejscu archeolodzy odkryli także najwcześniejsze sztuczne oko, które kiedyś wyglądało hipnotycznie na twarzy starożytnej kobiecej kapłanki lub wróżbity. Przez wieki rzuty kostką służyły do nauczania prawdopodobieństwa. Dla pojedynczego rzutu n-boczną kostką z inną liczbą na każdej powierzchni, prawdopodobieństwo rzucania dowolnej wartości jest 1/n. Prawdopodobieństwo przetaczania określonej sekwencji liczb to 1/ni. Na przykład, szansa na rzucenie I, a następnie 4 tradycyjną kostką to 1/62 = 1/36. Przy użyciu dwóch tradycyjnych kostek, prawdopodobieństwo wyrzucenia dowolnej sumy jest liczbą sposobów podzielenia tej sumy przez całkowitą liczbę kombinacji , dlatego suma 7 jest dużo bardziej prawdopodobna niż suma 2
Legendy sugerują, że magiczne kwadraty powstały w Chinach i po raz pierwszy zostały wymienione w manuskrypcie z czasów cesarza Yu, około 2200 roku p.n.e. Magiczny kwadrat składa się z pól N2, zwanych komórkami, wypełnionych liczbami całkowitymi, które są różne. Sumy liczb w poziomych rzędach, pionowych kolumnach i głównych przekątnych są równe. Jeśli liczby całkowite w magicznym kwadracie są kolejnymi liczbami od I do N2, kwadrat jest uważany za N-tego rzędu, a liczba magiczna lub suma każdego rzędu jest stała równa N(N2 + 1)/2 . Renesansowy artysta Albrecht Durer stworzył ten cudowny kwadrat magiczny 4 x 4 poniżej w 1514 roku.
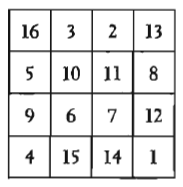
Zauważ, że dwie centralne liczby w dolnym wierszu brzmią "1514", rok budowy. Wiersze, kolumny i główne przekątne sumują się do 34. Ponadto 34 jest sumą liczb kwadratów narożnych (16 + 13 + 4 + I) i centralnego kwadratu 2 x 2 (10 + II + 6 + 7). Już w 1693 roku 880 magicznych kwadratów czwartego rzędu opublikowano pośmiertnie w "Des quassez ou tables magiques" autorstwa Bernarda Frenicle de Bessy, wybitnego amatorskiego francuskiego matematyka i jednego z czołowych magicznych badaczy wszechczasów. Przeszliśmy długą drogę od najprostszych magicznych kwadratów 3 x 3 czczonych przez cywilizacje niemal każdego okresu i kontynentu, od Indian Majów po ludność Hasua w Afryce. Dzisiaj matematycy badają te magiczne przedmioty w dużych wymiarach, na przykład w postaci cztero wymiarowych hipersześcianów, które mają magiczne sumy we wszystkich odpowiednich kierunkach.
George Arthur Plimpton (1855-1936)
Plimpton 322 odnosi się do tajemniczej babilońskiego talbiczki glinianej zawierającego cyfry w cunei ˇ formie skryptu w tabeli 4 kolumn i 15 rzędów. Eleanor Robson, historyk nauki, nazywa ją "jednym z najsławniejszych na świecie artefaktów matematycznych". Napisany około 1800 roku B.C., w tabeli wymieniono trójki pitagorejskie - czyli liczby całkowite określające długości boków trójkątów prostych, które są rozwiązaniami twierdzenia Pitagorasa : a2 + b2 = c2. Na przykład liczby 3,4 i 5 są potrójnymi pitagorejskimi. Czwarta kolumna w tabeli zawiera po prostu numer wiersza. Interpretacje różnią się co do dokładnego znaczenia liczb w tabeli, a niektórzy uczeni sugerują, że liczby były rozwiązaniami dla studentów studiujących algebrę lub problemy podobne do trygonometrii. Nazwa Plimpton 322 pochodzi od wydawcy z Nowego Jorku George′a Plimptona, który w 1922 roku kupił tabliczkę od sprzedawcy za 10 USD, a następnie przekazał ją do Columbia University. Tabliczkę można przypisać do cywilizacji starobabilońskiej, która rozkwitła w Mezopotamii, żyznej dolinie rzek Tygrys i Eufrat, która obecnie znajduje się w Iraku. Aby spojrzeć na epokę, nieznany skryba, który wygenerował Plimptona 322, żył w ciągu około stu lat od króla Hammurabiego, słynącego z zestawu praw, które zawierały "oko za oko, ząb za ząb". Według historii biblijnej, Abraham, który rzekomo poprowadził swój lud na zachód od miasta Ur, na brzeg Eufratu do Kanaanu, byłby kolejnym współczesnym pisarzowi. Babilończycy pisali na mokrej glinie, wciskając rysik lub klin w glinę. W systemie liczb babilońskich numer I został napisany jednym uderzeniem, a liczby od 2 do 9 zostały napisane przez połączenie wielokrotności pojedynczego wciśnięcia
Ahmes (ok. 1680 p.n.e., 1620 pne), Alexander Henry Rhind (1833-1863)
Papirus Rhinda jest uważany za najważniejsze znane źródło informacji dotyczących starożytnej egipskiej matematyki. Ten zwój o wysokości około 30 centymetrów i długości 5,5 m znaleziono w grobowcu w Tebach na wschodnim brzegu Nilu. Ahmes, pisarz, napisał to hieratycznie, skrypt związany z systemem hieroglifów . Biorąc pod uwagę, że pisanie miało miejsce około 1650 roku p.n.e., czyni to Ahmesa najwcześniej nazwaną jednostką w historii matematyki! Zwój zawiera także najwcześniejsze znane symbole operacji matematycznych - plus jest oznaczony przez parę stąpnięć idących w kierunku liczby, która ma zostać dodana. W 1858 r. Szkocki prawnik i egiptolog Alexander Henry Rhind odwiedził Egipt z powodów zdrowotnych, gdy kupił zwój na rynku w Luksorze. British Museum w Londynie nabyło zwój w 1864 roku. Ahmes napisał, że zwój zawiera "dokładne rozrachunki dotyczące wykorzystania rzeczy i wiedzy o wszystkich rzeczach, tajemnicach ... wszystkich tajemnicach". Treść zwoju dotyczy problemów matematycznych obejmujących ułamki, postępy arytmetyczne, algebrę i geometrię piramidy, a także praktyczną matematykę przydatną do pomiarów, budowania i księgowania. Najbardziej intryguje mnie problem 79, którego interpretacja początkowo była kłopotliwa. Dzisiaj wielu interpretuje Problem 79 jako zagadkę, którą można przetłumaczyć jako "Siedem domów zawiera siedem kotów, każdy kot zabija siedem myszy, każda z nich zjadła siedem kłosów, każde ucho zboża wyprodukowało siedem hekatów (miar) pszenica. Jaka jest ich suma? "Co ciekawe, ten niezniszczalny memem łamigłówki, zawierający liczbę 7 i zwierzęta, zdaje się utrzymywać przez tysiące lat! Obserwujemy coś bardzo podobnego w Liber Abaci (Fibonacci) opublikowanej w 1202 roku , a później w puzzle St Ives, staroangielskiej rymowanki dla dzieci z udziałem 7 kotów. Papirus Rhindda jest najważniejszym źródłem informacji o starożytnej egipskiej matematyce. Zwój. którego część jest tutaj pokazana, obejmuje problemy matematyczne związane z frakcjami, algorytmem arytmetycznym, algebrą. geometria i rachunkowość
Gra w Kółko i Krzyżyk (KK) jest jedną z najbardziej znanych i najstarszych gier ludzkości. Chociaż dokładna data KK z jego regułami może być stosunkowo nowa, archeolodzy mogą wyśledzić to, co wydaje się być grami z rzędu w rzędzie od starożytnego Egiptu około 1300 p.n.e., i podejrzewam, że podobne rodzaje gier powstały na samym początku świtu społeczeństwa. W przypadku KK dwaj gracze, stawiają 0 i X, na zmianę ,zaznaczają swoje symbole w przestrzeniach siatki 3 X 3. Gracz, który jako pierwszy stawia trzy swoje własne znaki w rzędzie poziomym, pionowym lub ukośnym, wygrywa. Losowanie zawsze można uzyskać dla planszy 3 x 3. W starożytnym Egipcie, w czasach wielkich faraonów, gry planszowe odgrywały ważną rolę w życiu codziennym, a gry typu KK są znane z tego, że grano w tych starożytnych czasach. KK może być uważany za "atom", na którym molekuły bardziej zaawansowanych gier pozycji zostały zbudowane przez wieki. Przy najdrobniejszych zmianach i rozszerzeniach prosta gra z KK staje się fantastycznym wyzwaniem, wymagającym znacznego czasu do opanowania. Matematycy i miłośnicy puzzli rozszerzyli KK na większe deski, wyższe wymiary i dziwne powierzchnie do grania, takie jak prostokątne lub kwadratowe tablice, które są połączone na krawędziach (kształt pączka) lub butelka Klein (powierzchnia tylko z jednej strony). Zastanów się nad ciekawostkami KK. Gracze mogą umieścić swoje X i O s na planszy KK w 9! = 362 880 sposobów. Istnieje 255,168 możliwych gier w KK, gdy weźmiesz pod uwagę wszystkie możliwe gry kończące się 5,6,7,8 i 9 ruchów. We wczesnych latach 80. XX wieku, komputerowi geniusze Danny Hillis, Brian Silverman i przyjaciele zbudowali Tinkertoya i komputer, który grał w KK. Urządzenie zostało wykonane z 10 000 części Tinkertoy. W 1998 roku badacze i studenci z Uniwersytetu w Toronto stworzyli robota do gry trójwymiarowej (4 x 4 x 4) KK z człowiekiem.
Baudhajana, Pitagoras z Samos
Dziś małe dzieci czasami słyszą najpierw słynne twierdzenie Pitagorasa z ust Stracha na Wróble, w filmowej wersji Czarnoksiężnika z Oz. Niestety, recytacja słynnego twierdzenia Stracha na Wróble jest całkowicie błędna! Twierdzenie Pitagorasa stwierdza, że dla każdego trójkąta prostokątnego kwadrat długości przeciwprostokątnej c jest równy sumie kwadratów na dwóch (krótszych) długościach "przyprostokątnych" a i b-, które są zapisane jako a2 + b2 = c2. Twierdzenie ma więcej opublikowanych dowodów niż jakikolwiek inne, a książka Elisha Scott "Loomis Pythagorean Proposition" zawiera 367 dowodów. Trójkąty Pitagorasa (PT) są trójkątami prostokątnymi o bokach całkowitych. Przyprostokątne "3-4-5" o długościach 3 i 4 oraz przeciwprostokątna o długości 5 to jedyne PT z trzema bokami jako kolejnymi liczbami i jedynym trójkątem o stronach całkowitych, którego suma boków (12) jest równa dwukrotnie jego powierzchnię (6). Po 3-4-5 PT następny trójkąt z kolejnymi długościami boków to 21-20-29. Dziesiąty taki trójkąt jest znacznie większy: 27304197- 27304196 -38613965. W 1643 r. Francuski matematyk Pierre de Fermat (1601-1665) poprosił o PT, tak aby zarówno przeciwprostokątna c, jak i suma (a + b) miały wartości kwadratowe. Zaskakujące było stwierdzenie, że najmniejsze trzy liczby spełniające te warunki to 4,565,486,077,761, 1,061,652,293,520 i 4,687,298,610,289. Okazuje się, że drugi taki trójkąt byłby tak "duży", że gdyby jego liczby były reprezentowane jako stopy, nogi trójkąta wystają z Ziemi ku Słońcu! Chociaż Pitagorasowi często przypisuje się sformułowaniu twierdzenia Pitagorasa, dowody sugerują, że twierdzenie zostało rozwinięte przez hinduskiego matematyka Baudhayana przed wiekami około 800 r. n.e/ w tekście Baudhayana Sulba Sutra. Trójkąty Pitagorasa były prawdopodobnie znane jeszcze wcześniej Babilończykom
Go to gra planszowa dla dwóch osób, która powstała w Chinach około 2000 roku p.n.e. Najwcześniejsze pisemne odniesienia do gry pochodzą z najwcześniejszego chińskiego dzieła historii narracji, Zuo Zhuan (Chronicle of Zuo), który opisuje człowieka w 548 r. p.n.e. który grał w tę grę. Gra rozprzestrzeniła się w Japonii, gdzie stała się popularna w XIII wieku. Dwóch graczy na przemian umieszcza czarne i białe kamienie na skrzyżowaniach planszy 19 x 19. Kamień lub grupa kamieni zostaje schwytana i usunięta, jeśli jest ciasno otoczona kamieniami o przeciwnych kolorach. Celem jest kontrolowanie większego terytorium niż przeciwnika. Go jest skomplikowany z wielu powodów, w tym z wielkiej planszy do gry, różnorodnych strategii i ogromnej liczby wariantów możliwych gier. Po prostu więcej kamieni niż przeciwnik nie zapewnia zwycięstwa. Po uwzględnieniu symetrii istnieje 32.940 ruchów otwierających. z których 992 uważa się za silne. Liczba możliwych konfiguracji plansz jest zwykle szacowana na 10172, z około 10768 możliwymi grami. Typowe gry pomiędzy utalentowanymi graczami składają się z około 150 ruchów, przy czym średnio wynosi około 250 wyborów na ruch. Choć potężne oprogramowanie szachowe jest w stanie pokonać najlepszych szachistów, najlepsze programy Go często gubią utalentowane dzieci. Granie w Go sprawia, że trudno jest "patrzeć do przodu" w grze, aby ocenić wyniki, ponieważ wiele bardziej racjonalnych ruchów musi być rozważanych w Go niż w szachach. Proces oceny preferencji pozycji jest również dość trudny, ponieważ różnica pojedynczego niezajętego punktu siatki może wpływać na duże grupy kamieni. W 2006 roku dwóch węgierskich badaczy poinformowało, że algorytm o nazwie UCT (dla górnych poziomów ufności zastosowanych do drzew) może konkurować z zawodowymi graczami Go, ale tylko na planszach 9 x 9. UCT pomaga komputerowi skoncentrować się na wyszukiwaniu obiecujących ruchów.
Około 530 roku p.n.e. grecki matematyk Pitagoras przeniósł się do Kroton we Włoszech, aby uczyć matematyki, muzyki i reinkarnacji. Chociaż wiele osiągnięć Pitagorasa mogło być zasługą jego uczniów, idee jego braterstwa od wieków wpływały na numerologię i matematykę. Pitagorasowi zazwyczaj przypisuje się odkrywaniu matematycznych związków związanych z harmoniami muzycznymi. Na przykład zauważył, że wibrujące struny wytwarzają harmonijne dźwięki, gdy proporcje długości strun są liczbami całkowitymi. Studiował także liczby trójkątne (oparte na wzorach kropek w kształcie trójkąta) i doskonałe liczby (liczby całkowite, które są sumą ich właściwych dzielników pozytywnych). Chociaż słynne twierdzenie, które nosi jego imię, a2 + b2 = c2 dla trójkąta prostokątnego z przyprostokątnymi a i b i przeciwprostokątną c, mogło być znane Hindusom i Babilończykom znacznie wcześniej, niektórzy uczeni sugerowali, że Pitagoras lub jego uczniowie należeli do pierwszych Greków, którzy to udowodnili. Pitagorasowi i jego zwolennikom liczby były jak bogowie, czyste i wolne od materialnych zmian. Czczenie liczb od 1 do 10 było rodzajem politeizmu dla pitagorejczyków. Wierzyli, że liczby są żywe, z telepatyczną formą świadomości. Ludzie mogliby zrezygnować z trójwymiarowego życia i telepatyzować z tymi istotami liczbowymi za pomocą różnych form medytacji. Niektóre z tych pozornie dziwnych pomysłów nie są obce współczesnym matematykom, którzy często debatują, czy matematyka jest dziełem ludzkiego umysłu, czy też jest po prostu częścią wszechświata, niezależną od ludzkiej myśli. Dla Pitagorejczyków matematyka była ekstatycznym objawieniem. Matematyczna i teologiczna mieszanka rozkwitła pod wpływem pitagorejczyków i ostatecznie wpłynęła na wiele filozofii religijnej w Grecji, odegrała rolę w religii średniowiecza i rozciągnęła się na współczesnego filozofa Immanuela Kanta. Bertrand Russell myślał, że gdyby nie Pitagoras, teologowie nie szukaliby tak często logicznych dowodów Boga i nieśmiertelności
Zenon z Elei (ok. 490 p.c.-430 p.n.e.)
Przez ponad tysiąc lat filozofowie i matematycy próbowali zrozumieć paradoksy Zenona, zestaw zagadek, które sugerują, że ruch powinien być niemożliwy lub że jest iluzją. Zenon był prokokratycznym greckim filozofem z południowych Włoch. Jego najsławniejszy paradoks dotyczy greckiego herosa Achillesa i powolnego żółwia, którego Achilles nigdy nie może wyprzedzić podczas wyścigu, gdy żółw dostanie przewagę. W rzeczywistości paradoks zdaje się sugerować, że nigdy nie możesz opuścić pomieszczenia, w którym się znajdujesz. Aby dotrzeć do drzwi, musisz najpierw przebyć tam połowę drogi. Będziesz także potrzebował kontynuować połowę pozostałej odległości, a druga połowa, i tak dalej. Nie dotrzesz do drzwi w skończonej liczbie skoków! Matematycznie można przedstawić ten limit nieskończonej sekwencji działań jako sumę serii (112 + 1/4 + 1/8 + ...). Jedną z tendencji modemów jest próba rozwiązania paradoksu Zenona przez naleganie, by suma tej nieskończonej serii 1/2 + 1/4 + 1/8 była równa I. Jeśli każdy krok jest wykonywany w połowie czasu, rzeczywisty czas do ukończenie nieskończonej serii nie różni się od czasu rzeczywistego wymaganego do opuszczenia pokoju. Jednak. takie podejście może nie zapewniać satysfakcjonującego rozwiązania, ponieważ nie wyjaśnia, w jaki sposób można zakończyć przechodzenie przez nieskończoną liczbę punktów, jeden po drugim. Dzisiaj matematycy używają nieskończenie małych (niewyobrażalnie małe ilości są prawie, ale nie całkiem zerowe), aby dostarczyć mikroskopijną analizę paradoksu. W połączeniu z branżą matematyki zwaną analizą niestandardową, a zwłaszcza wewnętrzną teorią mnogości, możemy rozwiązać paradoks, ale debata trwa. Niektórzy twierdzili również, że jeśli przestrzeń i czas są dyskretne, całkowita liczba skoków z jednego punktu do drugiego musi być skończona.
Hipokrates z Chios (około 470 p.C.-400. C.)
Starożytni greccy matematycy byli oczarowani pięknem, symetrią i porządkiem geometrii. Ulegając tej namiętności, grecki matematyk Hipokrates z Chios pokazał, jak skonstruować kwadrat o powierzchni równej określonej lunie. Lune to obszar w kształcie półksiężyca, ograniczony dwoma wklęsłymi łukami, a kwadratura z Lune jest jednym z pierwszych znanych dowodów w matematyce. Innymi słowy. Hipokrates wykazał, że obszar tych wydm można wyrazić dokładnie jako obszar prostoliniowy, czyli "kwadraturowy". W przedstawionym tutaj przykładzie dwa żółte wydmy związane z bokami trójkąta prostokątnego mają łączny obszar równy obszarowi trójkąta. Dla starożytnych Greków znalezienie kwadratury oznaczało użycie prostownicy i kompasu do skonstruowania kwadratu o powierzchni równej podanemu kształtowi. Jeśli taka konstrukcja jest możliwa, mówi się, że kształt jest "czworokątny" (lub "nadający się do kwadratu"). Grecy dokonali kwadratury wielokątów, ale zakrzywione formy były trudniejsze. W rzeczywistości z początku wydawało się nieprawdopodobne, by zakrzywione przedmioty mogły być w ogóle quadrable. Hipokrates słynie również ze skompilowania pierwszej znanej zorganizowanej pracy nad geometrią, prawie sto lat przed Euklidesem. Euklides mógł wykorzystać niektóre z pomysłów Hipokratesa we własnej pracy, Elemeny. Pisma Hipokratesa były znaczące, ponieważ stanowiły wspólne ramy, na których mogli budować inni matematycy. Próba Luna Hipokratesa była częścią wysiłku badawczego mającego na celu osiągnięcie "kwadratury koła" - czyli skonstruowania kwadratu o tym samym obszarze co koło. Matematycy próbowali rozwiązać problem "kwadratury koła" przez ponad 2000 lat, dopóki Ferdynand von Lindemann w 1882 roku nie udowodnił, że jest to niemożliwe. Dziś wiemy, że istnieje tylko pięć rodzajów lune, które są quadrable. Trzy z nich zostały odkryte przez Hipokratesa, a dwa kolejne znaleziono w połowie lat siedemdziesiątych
Platon (około 428 p.n.e.- 348 p.n.e)
Bryła platońska jest wypukłym, wieloaspektowym obiektem trójwymiarowym, którego powierzchnie są identycznymi wielobokami, o bokach równej długości i kątach równych stopni. Platoniczna bryła ma również taką samą liczbę twarzy spotykanych przy każdym wierzchołku. Najbardziej znanym przykładem bryły platońskiej jest sześcian, którego twarze mają sześć identycznych kwadratów. Starożytni Grecy rozpoznali i udowodnili, że można zbudować tylko pięć brył platońskich: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Na przykład dwudziestościan ma 20 twarzy, wszystkie w kształcie trójkątów równobocznych. Platon opisał pięć platońskich ciał stałych w Timaeusie w około 350 p.n.e. Był nie tylko zdumiony ich pięknem i symetrią, ale także wierzył, że kształty opisują struktury czterech podstawowych elementów, które uważały za komponujące kosmos. W szczególności czworościan był kształtem, który reprezentował ogień, być może z powodu ostrych krawędzi wielościanu. Oktaedron był powietrzem. Woda składała się z icosahedrów, które są gładsze niż inne platońskie ciała stałe. Ziemia składała się z kostek, które wyglądają solidnie. Platon zdecydował, że Bóg użył dwunastościanu do zorganizowania konstelacji w niebiosach. Pitagoras z Samos - słynny matematyk i mistyk, który żył w czasach Buddy i Konfucjusza, około 550 lat p.n.e. - prawdopodobnie znał trzy z pięciu brył platońskich (sześcian, czworościan i dwunastościan). Lekko zaokrąglone wersje platońskich brył z kamienia zostały odkryte na obszarach zamieszkałych przez mieszkańców późnego neolitu Szkocji co najmniej 1000 lat przed Platona. Niemiecki astronom Johannes Kepler (1571-1630) skonstruował modele brył platońskich zagnieżdżonych w sobie nawzajem, próbując opisać orbity planet o słońcu. Chociaż teorie Keplera były błędne, był on jednym z pierwszych naukowców, którzy nalegali na geometryczne wyjaśnienie zjawisk niebieskich.
Arystoteles (384 p.n.e. - 322 p.n.e.)
Arystoteles był greckim filozofem i naukowcem, uczniem Platona i nauczycielem Aleksandra Wielkiego. Organon (instrument) odnosi się do kolekcji sześciu dzieł Arystotelesa o logicei: Kategorie, Wcześniejsze analizy, De Interpretatione, Analityka posteriori, Odwołania sofistyki i Tematy. Andronik z Rodos zdecydował o uporządkowaniu sześciu dzieł około 40 p.n.e. Chociaż Platon (około 428 - 348 r.) I Sokrates (około 470- 399 r.) Zagłębili się w logiczne tematy, Arystoteles usystematyzował badania nad logiką, która przez 2000 lat dominowała w świecie zachodnim w naukowym rozumowaniu. Celem Organonu nie jest mówienie czytelnikom, co jest prawdą, ale raczej dawanie podejścia do tego, jak badać prawdę i jak rozumieć świat. Podstawowym narzędziem w zestawie narzędzi Arystotelesa jest sylogizm, trzystopniowy argument, taki jak "Wszystkie kobiety są śmiertelne, Kleopatra to kobieta, dlatego Kleopatra jest śmiertelna". Te dwie przesłanki są prawdziwe, wiemy, że wniosek musi być prawdziwy. Arystoteles dokonał także rozróżnienia między konkretami a uniwersami (kategorie ogólne). Kleopatra jest szczególnym domem. Kobieta i śmiertelnik są kategoriami uniwersalnymi. Arystoteles przeanalizował wiele możliwych rodzajów sylogizmów i pokazał, które z nich są prawidłowe. Arystoteles rozszerzył również swoją analizę na sylogizmy, które obejmowały logikę modalną, czyli wyrażenia zawierające słowa "ewentualnie" lub "koniecznie". Modemowa logika matematyczna może odejść od metodologii Arystotelesa lub rozszerzyć jego pracę na inne rodzaje struktur zdań, w tym wyrażające bardziej złożone relacje lub zawierające więcej niż jeden kwantyfikator, takie jak "Żadna kobieta jak wszystkie kobiety, które nie lubią niektórych kobiet". Niemniej jednak rozważa się systematyczną próbę rozwoju logiki Arystotelesa być jednym z największych osiągnięć ludzkości, dostarczając wczesnego impetu dla dziedzin matematyki, które są w ścisłym związku z logiką, a nawet wpływają na teologów w dążeniu do zrozumienia rzeczywistości.
Paradoks koła Arystotelesa jest wspomniany w starożytnym greckim tekście Mechanica. Problem prześladuje niektórych największych matematyków od stuleci. Rozważmy małe kółko zamontowane na dużym kole, przedstawione dwoma współśrodkowymi kołami. Jednopozycyjna korespondencja istnieje pomiędzy punktami większego okręgu i tymi na mniejszym okręgu; to znaczy, dla każdego punktu w dużym kole, jest dokładnie jeden punkt na małym okręgu i na odwrót. W ten sposób można oczekiwać, że zespół kół pokona tę samą odległość poziomą, niezależnie od tego, czy jest ona walcowana na pręcie, który dotyka mniejszego koła lub walcowane wzdłuż dolnego koła, które dotyka drogi. Ale jak to może być? W końcu wiemy, że dwa obwody okręgów są różne. Dziś matematycy wiedzą, że zgodność punktów jeden do jednego nie oznacza, że dwie krzywe muszą mieć taką samą długość. Georg Cantor (1845-1918) wykazał, że liczba punktów na liniach o dowolnej długości jest taka sama. Nazwał tę transfinitę liczby punktów "kontinuum". Na przykład wszystkie punkty w segmencie od zera do jednego można nawet umieścić w relacji jeden do jednego ze wszystkimi punktami nieskończonej linii. Oczywiście przed dziełem Cantora matematycy mieli dość trudny okres z tym problemem. Zwróć też uwagę, że z fizycznego punktu widzenia, jeśli duże koło toczyło się po drodze, mniejsze koło przeskakiwało i było przeciągane wzdłuż linii, która dotyka jego powierzchni. Dokładna data i autorstwo Mechanica może na zawsze być spowita tajemnicą. Choć często przypisuje się to jako dzieło Arystotelesa, wielu badaczy wątpi, że Mechanica, najstarszy znany podręcznik inżynierii, został faktycznie napisany przez Arystotelesa. Innym możliwym kandydatem do autorstwa jest student Arystotelesa Straton z Lampsacus (znany również jako Strato Physicus), który zmarł około 270 lat p.n.e.
Euklides z Aleksandrii mieszkał w hellenistycznym Egipcie, a jego książka "Elementy" jest jednym z najbardziej udanych podręczników w historii matematyki. Jego prezentacja geometrii płaskiej opiera się na twierdzeniach, które można wyprowadzić z prostych aksjomatów na żywo lub postulatów, z których jednym jest to, że można wybrać tylko jedną linię prostą między dowolnymi dwoma punktami. Biorąc pod uwagę punkt i linię, inny słynny postulat sugeruje, że tylko jedna linia przechodzi przez punkt. W latach osiemdziesiątych matematycy badali w sposób jawny geometrie nieeuklidesowe, w których równoległy postulat nie był już zawsze wymagany. Metodyczne podejście Euklides do udowodnienia twierdzeń matematycznych za pomocą logicznego rozumowania nie tylko stanowiło podstawę geometrii, ale także ukształtowało niezliczone inne obszary dotyczące dowodów logicznych i matematycznych. Elementy składają się z 13 tomów, które obejmują dwu- i trójwymiarowe geometrie, proporcje i teorię liczb. Elementy były jedną z książek , które zostaną wydrukowane po wynalezieniu prasy drukarskiej i były używane przez stulecia w ramach uniwersyteckich programów nauczania. Ponad 1000 wydań Elementów zostało opublikowanych od czasu ich pierwotnego druku w 1482 roku. Chociaż Euklides prawdopodobnie nie był pierwszym, który udowodnił różne wyniki w Elementach jego przejrzysta organizacja i styl sprawiły, że praca stała się trwała. Matematyczny historyk Thomas Heath nazwał Elementy "największym podręcznikiem matematycznym wszechczasów". Naukowcy tacy jak Galileo Galilei i Isaac Newton byli pod silnym wpływem elementów. Filozof i logik Bertrand Russell pisał: "W wieku jedenastu lat zacząłem czytać Euklidesa, z moim bratem jako nauczycielem. To było jedno z wielkich wydarzeń w moim życiu, oślepiając miłość . Nie wyobrażałem sobie, że na świecie jest coś tak pysznego". Poeta Edna St. Vincent Millay napisał: "Sam Euklides patrzył na nagie Piękno".
W 1941 r. Matematyk GH Hardy napisał: "Archimedes zostanie zapamiętany, gdy [dramaturg] Ajschylosa zostanie zapomniany, ponieważ języki umierają, a matematyczne idee nie są nieśmiertelnością", może to być głupie, ale prawdopodobnie matematyk ma największe szanse na zapamiętanie . Istotnie, Archimedes, starożytny grecki geometra, jest często uważany za największego matematyka i naukowca starożytnego i jednego z czterech największych matematyków, którzy chodzili po Ziemi - razem z Izaakiem Newtonem, Carlosem Friedrichem Gaussem i Leonhardem Eulerem. Co ciekawe, Archimedes czasami wysyłał kolegom fałszywe twierdzenia, aby złapać ich w pułapkę, gdy ukradli jego pomysły. Oprócz wielu innych matematycznych pomysłów słynie z kontemplacji ogromnej liczby osób. W swojej książce The Sand Reckoner Archimedes oszacował, że 8 x 1063 ziaren piasku wypełni wszechświat. Bardziej zadziwiająco, liczba 7.760271406486818269530232833213 ... x 10202544 jest rozwiązaniem jednej z wersji słynnego "problemu bydła" Archimedesa; która polega na obliczeniu całkowitej liczby sztuk bydła w układance dotyczącej czterech hipotetycznych stad o różnych kolorach, Archimedes napisał, że każdy, kto mógłby rozwiązać problem, będzie "koronowany na chwałę" i zostanie "uznany za doskonałego w tym gatunku mądrości". Aż do 1880 r. matematycy dawali przybliżoną odpowiedź, dokładniejsza liczba została po raz pierwszy obliczona w 1965 r. przez kanadyjskich matematyków Hugha C. Williamsa, niemieckiego RA i C. Roberta Zamke&prime przy użyciu komputera IBM 7040. W 2003 r. Historycy matematyki odkryli dawno zaginione informacje na temat Stomachion Archimedesa W szczególności, stary pergamin, nadpisany przez mnichów prawie tysiąc lat temu, opisuje Łagodny Łokieć Archimedesa, układankę z kombinatoryką, kombinatoryka to dziedzina matematyki zajmująca się wieloma sposobami rozwiązania danego problemu. celem Stomachion jest ustalenie, na ile sposobów 14 fragmentów tutaj może zostać zestawionych w celu utworzenia kwadratu. W 2003 roku czterej matematycy ustalili, że liczba to to 17,152.
Pi, symbolizowane przez grecką literę π ,jest, to stosunek obwodu koła do jego średnicy i jest w przybliżeniu równa 3,14159. Być może starożytne narody zauważyły, że na każdy obrót koła wozu porusza się do przodu około trzykrotnie więcej od średnicy koła - wczesne rozpoznanie, że obwód to jest około trzy razy średnica. Starożytna tablica babilońska stwierdza, że stosunek obwodu koła do obwodu wpisanego sześciokąta wynosi od 1 do 0,96, co oznacza wartość pi równą 3,125. Metaforyczny archeolog, Archimedes (ok. 250 p.n.e.), jako pierwszy dał nam matematycznie rygorystyczny zakres dla π - wartości od 223/71l do 22/7. Walijski matematyk William Jones (1675-1749) wprowadził symbol. π w 1706, najprawdopodobniej od greckiego słowa o peryferiach, które zaczynają się wraz z literą. π Najbardziej znane π w matematyce to Ziemia i prawdopodobnie dla jakiejkolwiek zaawansowanej cywilizacji we wszechświecie. Cyfry π nigdy się nie kończą, ani nikt nie wykrył uporządkowanego wzorca w ich aranżacji. Szybkość, z jaką komputer może obliczyć. π jest ciekawą miarą zdolności obliczeniowych komputera, a dziś wiemy ponad bilion cyfr . Zazwyczaj kojarzymy π z okręgiem, podobnie jak ludzkość sprzed siedemnastego wieku. Jednak w siedemnastym ośrodku 1T został uwolniony z koła. Było wiele krzywych wynalezionych i zbadanych (na przykład różne łuki, hypocykloidy i krzywe znane jako wiedźmy) i stwierdzono, że ich obszary mogą być wyrażone w terminach. Ostatecznie π wydawało się, że całkowicie uciekną z geometrii, a dzisiaj π odnosi się do niewytłumaczalnie wielu obszarów teorii liczb, prawdopodobieństwa, liczb zespolonych i szeregu prostych ułamków takich jak π / 4 = 1 - 1/3 + 1/5 - 1/7 .. .. W 2006 Akira Haraguchi, emerytowany japoński inżynier, ustanowił rekord świata do zapamiętywania i recytowania 100 000 cyfr π
Liczba pierwsza jest liczbą większą niż 1, taką jak 5 lub 13, która jest podzielna tylko samą siebie lub 1. Liczba 14 nie jest liczbą pierwszą, ponieważ 14 = 7 x 2. Liczby pierwsze fascynowały matematyków od ponad dwóch tysięcy lat. Około 300 lat p.n.e. Euklides wykazał, że nie ma "największej liczby pierwszej" i że istnieje nieskończenie wiele liczb pierwszych. Ale jak możemy ustalić, czy liczba jest liczbą pierwszą? Około 240 r. p.n.e. grecki matematyk Eratostenes opracował pierwszy znany test na pierwotność, który dzisiaj nazywamy Sito Eratostenesa. W szczególności Sito może być użyte do znalezienia wszystkich liczb pierwszych do określonej liczby całkowitej. (Zawsze wszechstronny Eratostenes służył jako dyrektor słynnej biblioteki w Aleksandrii i był również pierwszą osobą, która zapewniła rozsądną ocenę średnicy Ziemi). Zafascynowany był również francuski teolog i matematyk Marin Mersenne (1588-1648) przez liczby pierwsze i próbował znaleźć formułę, której mógłby użyć do znalezienia wszystkich liczb pierwszych. Chociaż nie znalazł takiej formuły, jego praca nad liczbami Mersenne′a postaci 2p - 1. gdzie p jest liczbą całkowitą, nadal nas interesuje. Liczby Mersenne′a, z p liczbą pierwszą, są najłatwiejszym typem liczby, aby udowodnić liczbę pierwszą, więc zwykle są to największe liczby pierwsze, o których ludzkość jest świadoma. Czterdziesta piąta znany liczba pierwsza Mersenne′a (243 112,609 -1) została odkryta w 2008 roku i zawiera 12 978 189 cyfr! Obecnie liczby pierwsze odgrywają ważną rolę w algorytmach kryptograficznych z kluczem publicznym, które mogą być używane do wysyłania bezpiecznych wiadomości. Co ważniejsze, dla czystych matematyków liczby pierwsze były w samym sercu wielu intrygujących nierozwiązanych przypuszczeń w historii, w tym Hipotezy Riemanna, która dotyczy rozkładu liczb pierwszych i silnej hipotezy Goldbacha, która stwierdza, że każdą parzystą liczbę całkowitą większą niż 2 można zapisać jako sumę dwóch liczb pierwszych.
Podobnie jak bryły platońskie, wielościany pół regularne Archimedesa (ASRP) są wypukłymi, wielowymiarowymi obiektami trójwymiarowymi, których ściany są wszystkimi regularnymi wielokątami o bokach równej długości i kątach równych stopni. Jednak w przypadku ASRP twarze są różnego rodzaju. Na przykład wielościan utworzony przez 12 pięciokątów i 20 sześciokątów, który przypomina nowoczesną piłkę do piłki nożnej, został opisany przez Archimedesa wraz z 12 innymi tego rodzaju wielościanami. Wokół każdego wierzchołka (narożnika) tego rodzaju brył, ten sam wielokąt pojawia się w tej samej sekwencji, na przykład sześciokąt-sześciokąt-trójkąt. Oryginalne pisma Archimedesa opisujące 13 ASRP zostały utracone i znane tylko z innych źródeł. W okresie renesansu artyści odkryli wszystko oprócz jednego ASRP. W 1619 roku Kepler przedstawił cały zestaw w swojej książce Harnonices Mundi (Harmonia świata). ASRP mogą być określone za pomocą zapisu numerycznego, który wskazuje kształty wokół wierzchołka. Na przykład 3,5,3,5 oznacza, że trójkąt, pięciokąt, trójkąt i pięciokąt pojawiają się w tej kolejności. Korzystając z tej notacji, mamy następujące ASRP: 3,4,3,4 (sześciokąt); 3,5.3,5 (dwunastościan ikozydowy); 3,6,6 (ścięty czworościan); 4,6,6 (ścięty ośmiościan); 3,8,8 (ścięta kostka); 5,6,6 (ścięty dwudziestościan, lub piłka nożna); 3,10,10 (ścięty dwunastościan); 3,4,4,4 (trójkątny romb); 4,6,8 (ścięty sześciokątny); 3,4,5,4 (dwunastościan rombowy); 4,6,10 (obcięty dwudziesto dwunastościan); 3,3,3,3,4 (sześcian snub lub sześciokątny snub); i 3,3,3,3,5 (dwunastościan o zwartej budowie lub dwunastościan zygzakowaty). Dwudziestościan ścięty o 32 płaszczyznach jest szczególnie fascynujący. Kształty piłek nożnych opierają się na bryle Archimedesa i była to również konfiguracja wykorzystywana do układania soczewek, które skupiały wybuchowe fale uderzeniowe detonatorów w bombie atomowej "Fat Man" zdetonowanej nad Nagasaki w Japonii podczas II wojny światowej. chemikom udało się stworzyć najmniejszą na świecie piłkę nożną, cząsteczkę węgla o 60 atomach na wierzchołkach ściętego dwudziestościanu, tak zwane Buckyballs mają fascynujące właściwości chemiczne i fizyczne, które są badane w zastosowaniach od smarowania po zabiegi AIDS.
Termin spirala jest często używany ogólnie do opisania dowolnej geometrycznie gładkiej krzywej, która wije się wokół centralnego punktu lub osi, jednocześnie oddalając się od niej. Kiedy myślimy o przykładach spirali, przychodzą na myśl zarówno przyziemne, jak i egzotyczne - delikatne zwijanie paprociowego wąsika, kształt wycofanego ramienia ośmiornicy, forma śmierci założona przez stonogę, spiralne jelito żyrafy, kształt języka motyla i spiralny przekrój zwoju. Spirale posiadają proste piękno, które ludzie skopiowali w swoich sztukach i narzędziach, a natura wykorzystała w tworzeniu wielu struktur życia. Matematyka najprostszej formy spiralnej, spirali Archimedesa, została po raz pierwszy omówiona przez Archimedesa w 225 r. p.n.e. w swojej książce On Spirals. Spirala ta może być wyrażona równaniem r = a + bΘ. Parametr a obraca całą spiralę, a b kontroluje odległość między kolejnymi zakrętami. Najczęściej obserwowane spirale są typu Archimedesa: mocno zwinięte sprężyny, krawędzie zwiniętych dywanów i dekoracyjne spirale na biżuterii. Praktyczne zastosowania spirali Archimedesa obejmują transfuzję ruchu obrotowego do liniowego w maszynach do szycia. Sprężyna spiralna Archimedesa jest interesująco pod względem zdolności reagowania na siłę skręcającą i translacyjną. Starożytne przykłady spirali Archimedesa obejmują prehistoryczne labirynty spiralne, wzory spirali z terakoty z VI wieku p.n.e.,, dekoracje ze starożytnych dzieł Ałtaju (połowa pierwszego tysiąclecia pne), ryciny na kamieniach progowych komór inicjacyjnych w epoce brązu w Irlandii, prace przewijania dla manuskryptów irlandzkich i dzieł Tanki Tybetańskiej, z których te ostatnie są malowane lub haftowane wzory buddyjskie czasami zawieszone w klasztorach. W rzeczywistości spirala jest wszechobecnym symbolem w starożytnym świecie. Jego częste występowanie w miejscach pochówku sugeruje, że symbol ten mógł reprezentować cykl życia, śmierci i odrodzenia, jak w przypadku ciągłego wznoszenia się i opadania słońca.
Cisoida Dioklesa została odkryta przez greckich matematyków Diokles, około 180 r. p.n.e., podczas jego prób wykorzystania jego niezwykłych właściwości do podwojenia sześcianu. "Podwojenie sześcianu" odnosi się do słynnego i starożytnego wyzwania polegającego na skonstruowaniu sześcianu o objętości dwukrotnie większej niż objętość danego mniejszego sześcianu, co oznacza, że większy sześcian ma krawędź pierwiastek trzeciego stopnia z dwóch razy większą niż pierwsza kostka. Używanie cisoid przez Diokles i ich przecięcie z linią prostą było teoretycznie poprawne, ale nie przestrzegało rygorystycznie zasad euklidesowej konstrukcji, która pozwalała na użycie tylko kompasu i prostej linii. Nazwa cisoida pochodzi od greckiego terminu oznaczającego "w kształcie bluszczu". Wykres krzywej rozciąga się do nieskończoności wzdłuż obu kierunków osi Y i ma pojedynczy wierzchołek. Obie gałęzie krzywej, które rozciągają się od wierzchołka, zbliżają się do tego samego asymptoty pionowej. Jeśli narysujemy okrąg przechodzący przez guzek w punkcie 0 i styczny do asymptoty, to dowolną linię łączącą guzek i punkt M na cisoidzie można przedłużyć tak, aby przecinał asymptotę w punkcie B. Długość odcinka wydłużenie liniowe od C do B jest zawsze równe długości od 0 do M. Krzywa może być wyrażona we współrzędnych biegunowych jako r = 2a(secΘ - cosΘ) lub we współrzędnych prostokątnych jako y2 = x3/(2a - x) . Co ciekawe, cisoida może być produkowany przez śledzenie wierzchołka paraboli, gdy toczy się, bez poślizgu, na drugiej paraboli o tym samym rozmiarze. Diokles był zafascynowany krzywiznami zwanymi stożkowymi, a w swojej pracy On Burning Mirrors omówił centralny punkt paraboli. Jednym z jego celów było znalezienie powierzchni lustra, która skupiałaby maksymalną ilość ciepła, gdy zostanie umieszczone w słońcu.
Matematyk i astronom Ptolemeusz z Aleksandrii napisał 13-tomowy Almagest, obszerny traktat na temat praktycznie wszystkich znanych aspektów astronomii. W Almagest Ptolemeusz zajmuje się pozornym ruchem planet i gwiazd. Jego geocentryczny model, w którym Ziemia znajduje się w centrum wszechświata, a Słońce i planety krążą wokół Ziemi, został uznany za prawidłowy przez ponad tysiąc lat w Europie i świecie arabskim. Almagest jest łacińską formą arabskiego imienia al-kitabu-l-mijisti (Wielka Księga), a praca ta jest szczególnie interesująca dla matematyków ze względu na jej zawartość trygonometryczną, która zawiera odpowiednik tabeli wartości sinusowych dla kątów od 0o do 90o w odstępach 15-minutowych i wprowadzenie do trygonometrii sferycznej. Almagest zawiera również twierdzenia, które odpowiadają naszemu nowoczesnemu "prawu sinusów" oraz tożsamościom złożonym i pół-kątowym. Ian Gullberg pisze: "Tak wiele wczesnych greckich prac nad astronomią zostało utraconych, może być wynikiem kompletności i elegancji prezentacji Almagesta Ptolemeusza, sprawiając, że wszystkie wcześniejsze prace wydają się zbędne". Gerd Grasshoff pisze: "Ptolemeusz Almagest dzieli się z elementami Euclida na chwałę bycia tekstem naukowym najdłużej używanym. Od poczęcia w drugim wieku do późnego renesansu. Dzieło to określało astronomię jako naukę," Almagest został przetłumaczony na arabski około roku 827, a następnie z arabskiego na łacinę w XII wieku. Perski matematyk i astronom Abu al-Wafa (940-998) zbudował na podstawie Almagesty usystematyzowane twierdzenia i dowody trygonometryczne. Co ciekawe, Ptolemeusz próbował obliczyć rozmiar wszechświata na podstawie swoich modeli ruchów planetarnych, w których planeta porusza się w małym okręgu, zwanym epicyklem, który z kolei porusza się po większym okręgu. Oszacował, że kula zawierająca odległe "gwiazdy stałe" była 20 000 razy większa od promienia Ziemi.
Grecki matematyk Diophantus z Aleksandrii, nazywany czasem "ojcem algebry"; był autorem Arithmetica (ok. 250), serii tekstów matematycznych, które od wieków wpływały na matematykę, arytmetyka, najbardziej drażliwa praca na temat algebry w całej greckiej matematyce, zawiera różne problemy wraz z numerycznymi rozwiązaniami równań. ważne z powodu jego postępów w notacji matematycznej i traktowania ułamków jako liczb. W dedykacji w Arithmetice, Diophantus pisze do Dionizosa (najprawdopodobniej biskupa Aleksandrii), że chociaż materiał w książce może być trudny, "będzie łatwy do uchwycenia, z twoim entuzjazmem i moim nauczaniem. "Różne dzieła Diophantusa zostały zachowane przez Arabów i przetłumaczone na łacinę w XVI wieku. Równania diofantyczne, z ich całkowitymi rozwiązaniami, są nazwane na jego cześć. Pierre de Fermat napisał swoje ostatnie twierdzenie Fermata dotyczące rozwiązań całkowitych an + bn = cn we francuskim tłumaczeniu arytmetycznym , opublikowanym w 1681 r. Arithmetica Diophantusa często była interesująca w znalezieniu rozwiązań całkowitych dla równań takich jak ax2 + bx = c. Mimo że Babilończycy byli świadomi pewnych metod rozwiązywania równań liniowych i kwadratowych, takich jak te, które zaszczepił Diophantus, Diophantus jest szczególny, zgodnie z D. Swift za to, że jest "pierwszym, który wprowadził obszerną i spójną algebraiczną notację reprezentującą ogromną poprawę w stosunku do czysto słownego stylu swoich poprzedników (i wielu następców) .... Ponowne odkrycie arytmetyki przez źródła bizantyjskie bardzo pomogło renesansowi matematyki w Europie Zachodniej i pobudził wielu matematyków, z których największym był Fermat ". Zauważmy, że perski matematyk al-Khwarizmi (780-850) również ma tytuł" ojca algebry " za swoją książkę Algebra, która zawierała systematyczne rozwiązanie równań liniowych i kwadratowych . Al-Khwarizrni wprowadził cyfry hinduistyczno-arabskie i koncepcje algebraiczne do matematyki europejskiej, a algorytm i algebra wyprowadzono odpowiednio z jego imienia i nazwiska al-jabr; Al-jabr to arabskie słowo dla operacji matematycznej używanej do rozwiązywania równań kwadratowych.
Rolnik chce posadzić dziewięć drzew klonu tak, aby tworzyły dziesięć prostych rzędów z trzema drzewami w każdym rzędzie. Jeden ciekawy sposób osiągnięcia swojego celu wykorzystuje twierdzenie Pappusa. Jeśli trzy punkty A, B, C znajdują się w dowolnym miejscu wzdłuż jednej linii, a trzy punkty D, E, Fare znajdują się gdziekolwiek na drugiej linii, twierdzenie Pappusa gwarantuje, że przecięcia X, Y, Z przeciwległych stron skrzyżowanego sześciokąta A, F, B, D, C, E leżą na linii prostej. Rolnik może rozwiązać swój problem i utworzyć dziesiąty rząd, przesuwając drzewo B, aby wyrównać B, Y i E. Pappus był jednym z najważniejszych hellenistycznych matematyków w jego wieku i słynącym z Synagogi (Kolekcji) napisanej w c. 340. Praca koncentruje się na tematach geometrii, które obejmują wielokąty, wielościany, koła, spirale i konstrukcję plastra miodu przez pszczoły. Synagoga jest również cenna, ponieważ zawiera wyniki oparte na starożytnych dziełach, które później zostały utracone. Thomas Heath pisze o Synagodze: "Oczywiście napisane w celu ożywienia klasycznej greckiej geometrii, obejmuje ona praktycznie całe pole". O słynnym twierdzeniu Pappusa Max Dehn pisze, że "oznacza ono zdarzenie w historii geometrii. Od początku geometria dotyczyła miar: długości orion, obszarów figur płaskich i objętości ciał. po raz pierwszy twierdzenie, które zostało potwierdzone przez zwykłą teorię miar, ale samo w sobie jest wolne od wszystkich elementów pomiarów. " Innymi słowy, twierdzenie demonstruje istnienie liczby, która jest określana tylko przez występowanie linii i punktów. Dehn mówi również, że ta liczba jest "pierwszą konfiguracją geometrii rzutowej". Synagoga stała się powszechnie znana w Europie po 1588 r., Kiedy wydrukowano łacińskie tłumaczenie Federico Commandino. Postać Pappusa zaintrygowała Izaaka Newtona i Rene Descartesa. Około 1300 lat po napisaniu przez Pappusa Synagogi francuski matematyk Blaise Pascal przedstawił interesujące uogólnienie twierdzenia Pappusa.
Rękopis Bakhshali jest znaną kolekcją matematyczną, odkrytą w 1881 roku w kamiennej obudowie w północno-zachodnich Indiach, a może nawet sięgać trzeciego wieku. Po jego odkryciu znaczna część rękopisu została zniszczona, a tylko około 70 liści kory brzozy przetrwało do czasu jego odkrycia. Manuskrypt Bakhshali zawiera techniki i zasady rozwiązywania problemów arytmetycznych, algebry i geometrii oraz dostarcza wzoru do obliczania pierwiastka kwadratowego. Oto jeden problem z manuskryptu: "Przed tobą jest grupa 20 osób składająca się z mężczyzn, kobiet i dzieci. Zarabiają między sobą 20 monet. Każdy mężczyzna zarabia 3 monety, każda kobieta 1,5 monety, a każde dziecko pół monety. Ilu jest mężczyzn, kobiet i dzieci? Czy potrafisz to rozwiązać? Rozwiązaniem okazuje się 2 mężczyzn, 5 kobiet i 13 dzieci. Możemy pozwolić, aby liczba mężczyzn, kobiet i dzieci wynosiła odpowiednio m, w i c. Dwie formuły opisują naszą sytuację: m + w + c = 20 i 3m + (3/2) w + (1/2) c = 20." Podane rozwiązanie jest jedynym ważnym. Rękopis został znaleziony w pobliżu wioski Bakshali w rejonie Yusufzai w dzielnicy Peszawar (obecnie w Pakistanie). Data rękopisu jest przedmiotem wielu dyskusji, jednak wielu uczonych uważa, że jest to komentarz do starszej pracy, która mogła istnieć około 200 do 400 r. n.e. Jedną z niezwykłych cech rękopisu Bakhshali jest użycie " Znaku + "umieszczonego po liczbie, aby wskazać negatyw. Równania są podane z dużą kropką reprezentującą nieznaną wartość, która jest poszukiwana. Podobna kropka służy do reprezentowania zera. Dick Teresi pisze: "Najważniejsze jest to, że rękopis Bakhshali jest pierwszym dokumentem przedstawiającym formę matematyki indyjskiej pozbawionej związków religijnych".
Hypatia z Aleksandrii została zamęczona przez chrześcijański tłum, częściowo, dlatego, że nie przestrzegała ścisłych zasad chrześcijańskich. Uważała się za neoplatonistkę, pogankę i zwolenniczkę pitagorejskich idei. Co ciekawe, Hypatia jest pierwszą matematyczką w historii ludzkości, o której dysponujemy dość bezpieczną i szczegółową wiedzą. Mówiono, że jest atrakcyjna fizycznie i zdecydowanie w celibacie. Zapytana, dlaczego ma obsesję na punkcie matematyki i nie wyjdzie za mąż, odpowiedziała, że jest przywiązana do prawdy. Prace Hypatii obejmują komentarze do Arithmeticd Diophantusa. W jednym ze swoich problemów matematycznych dla uczniów poprosiła ich o całkowite rozwiązanie pary równań równoczesnych: x - y = a i x2 - y2= (x - y) + b, gdzie a i b są znane. Czy można znaleźć dowolne wartości całkowite dla x, y, a i b, które czynią oba te formuły prawdziwymi? Chrześcijanie byli jej najsilniejszymi filozoficznymi rywalami i oficjalnie zniechęcili do jej platońskich twierdzeń o naturze Boga i życia po śmierci. W ciepły dzień marca w AD. 414, tłum chrześcijańskich zelotów chwycił ją, rozebrał i zaczął drapać jej ciało do kości za pomocą ostrych muszli. Następnie pocięli jej ciało i spalili kawałki. Podobnie jak niektóre ofiary dzisiejszego terroryzmu religijnego, mogła zostać przejęta tylko dlatego, że była sławną osobą po drugiej stronie podziału religijnego. Dopiero po renesansie inna kobieta, Maria Agnesi, zyskała miano sławnego matematyka. Śmierć Hypatii spowodowała odejście wielu uczonych z Aleksandrii i pod wieloma względami oznaczała koniec wieków greckiego postępu w matematyce. Podczas europejskich ciemnych wieków Arabowie i Hindusi odgrywali wiodącą rolę w rozwijaniu postępu w matematyce
Brahmagupta (ok. 598 - ok. 668), Bhaskara (ok. 6OO - ok. 680), Mahavira (ok. 800-c. 870)
Starożytni Babilończycy początkowo nie mieli symbolu zera, co powodowało niepewność w ich notacji, tak jak dzisiaj bylibyśmy zdezorientowani, gdyby liczby takie jak 12, 102 i 1002 nie miały zera, aby je odróżnić. Babilońscy skrybowie zostawili tylko miejsce, w którym powinno być zero, i nie było łatwo odróżnić liczbę pól w środku lub na końcach liczb. Ostatecznie Babilończycy wymyślili symbol oznaczający lukę między ich cyframi, ale prawdopodobnie nie mieli pojęcia zera jako rzeczywistej liczby. W okolicach A.D. 650 użycie tej liczby było powszechne w matematyce indyjskiej a kamienna tablica została znaleziona w Gwalior, na południe od Delhi, z numerami 270 i 50. Liczby na tabliczce datowane na AD. 876, wyglądają bardzo podobnie do numerów modemów, z tym że zera są mniejsze i podniesione. Indyjscy matematycy tacy jak Brahmagupta, Mahavira i Bhaskara używali zera w operacjach matematycznych. Na przykład Brahmagupta wyjaśnił, że liczba odjęta od siebie daje zero i zauważył, że każda liczba pomnożona przez zero wynosi zero. Rękopis Bakhshali może być pierwszym udokumentowanym dowodem zerowym używanym do celów matematycznych, ale jego data jest niejasna. Około AD. 665, cywilizacja Majów w Ameryce Środkowej również rozwinęła liczbę zero, ale jej osiągnięcie nie miało wpływu na inne ludy. Z drugiej strony indyjska koncepcja zera rozprzestrzeniła się na Arabów, Europejczyków i Chińczyków i zmieniła świat. Matematyk Hossein Arsbam pisze: "Wprowadzenie zera do systemu dziesiętnego w XIII wieku było najważniejszym osiągnięciem w rozwoju systemu liczbowego, w którym obliczenia z dużymi liczbami stały się wykonalne. Bez pojęcia zera, … procesy modelowania w handlu, astronomii, fizyce, chemii i przemyśle byłyby nie do pomyślenia. Brak takiego symbolu jest jedną z poważnych wad rzymskiego systemu liczbowego. "
Alkuin of York (ok. 735- 804), Gerbert z Aurillac (ok. 946-1003) Flaccus Albinus Alcuinus, znany również jako Alcuin z Yorku, był uczonym z Yorku w Anglii. Na zaproszenie króla Karola Wielkiego został wiodącym nauczycielem na dworze Karolingów, gdzie pisał traktaty teologiczne i wiersze. Był opatem Opactwa św. Marcina w Tours w 796 r., A przede wszystkim uczonym odrodzenia nauki znanego jako Renesans Karolingów. Uczeni spekulują, że jego książka matematyczna Propositiones ad acuendos juvenes (Problemy z wyostrzaniem młodych) przyczyniła się do edukacji ostatniego papieża - matematyka, Gerbert z Aurillac, zafascynowanego matematyką i wybrany na papieża Sylwestra II w 999 roku. Zaawansowana znajomość matematyki tego papieża przekonała niektórych jego wrogów, że jest złym magiem. W mieście Reims we Francji "papież liczbowy" przekształcił podłogę katedry w gigantyczne liczydło. Przyjął także cyfry arabskie (1, 2, 3,4,5,6,7,8 i 9) jako zamiennik cyfr rzymskich. Przyczynił się do wynalezienia zegara wahadłowego, wymyślił urządzenia śledzące orbity planetarne i pisał o geometrii. Kiedy zdał sobie sprawę, że brakuje mu wiedzy fonnallogicznej, studiował u logików Cennana. Papież powiedział: "Sprawiedliwy żyje wiarą, ale dobrze, że powinien łączyć naukę ze swoją wiarą". Alcunius′s Propositiones zawierał około 50 problemów słownych z rozwiązaniami, z których najbardziej znane to przeprawy przez rzekę, liczenie gołębi na drabinie, umierający ojciec opuszczający naczynia z winami dla swoich synów i trzech zazdrosnych mężów, z których każdy nie może pozwolić drugiemu człowiekowi bądź sam z żoną. Kilka głównych klas problemów pojawia się po raz pierwszy w Propositiones. Pisarz matematyki Ivars Peterson zauważa, że liczba problemów (i rozwiązań) w Propositiones zapewnia fascynujące przebłyski różnych aspektów życia w średniowieczu i świadczy o trwałej mocy zagadek w edukacji matematycznej.
Abu, a′far Muhammad ibn Musa al-Khwarizmi (ok. 78O - ok. 850) Al-Khwarizmi był perskim matematykiem i astronomem, który spędził większość swojego życia w Bagdadzie. Jego książka o algebrze, Kitab al-mukhtasar Ii hisab al-iabr wa''l-muqabala była pierwszą książką o systematycznym rozwiązywaniu równań liniowych i kwadratowych i czasami jest określana przez skrócony tytuł Algebra. Wraz z Diophantusem uważany jest za "ojca algebry". Łacińskie tłumaczenie jego prac wprowadziło dziesiętny system pozycyjny do Europy. Co ciekawe, słowo algebra pochodzi z al- abr, jednej z dwóch operacji użytych w jego książce do rozwiązywania równań kwadratowych. Dla al-Khwarizmi, al-jabr jest metodą, w której możemy wyeliminować ujemne ilości w równaniu, dodając tę samą ilość do każdej strony. Na przykład możemy zmniejszyć x2 = 50x - 5x2 do 6x2 = 50x, dodając 5x2 do obu stron. Al-muqabala jest metodą, dzięki której zbieramy ilości tego samego typu na tej samej stronie równania. Na przykład, x2 + 15= x + 5 jest redukowane do -x2 + 10 = x. Książka pomogła czytelnikom w rozwiązaniu równań takich jak formy x2 + 10x = 39, x2 + 21 = 10x i 3x + 4 = x2, ale bardziej ogólnie al-Khwarizmi uważał, że trudne problemy matematyczne można rozwiązać, jeśli zostaną złamane w serię mniejszych kroków. Al-Khwarizmi chciał, aby jego książka była praktyczna, pomagając ludziom w obliczeniach dotyczących pieniędzy, dziedziczenia nieruchomości, procesów sądowych, handlu i kopania kanałów. Jego książka zawierała również przykładowe problemy i rozwiązania. Al-Khwarizmi przez większość swojego życia pracował w Domu Mądrości w Bagdadzie, bibliotece, instytucie tłumaczeń. i miejscu nauki, które było głównym ośrodkiem intelektualnym islamskiego złotego wieku. Niestety, Mongołowie zniszczyli Dom Mądrości w 1258 roku, a legenda głosi, że wody Tygrysu popłynęły czarnym atramentem z książek rzucanych w jego wody.
Prosty, ale intrygujący zestaw powiązanych ze sobą przedmiotów interesujących matematyków i chemików tworzący pierścienie Boromejskie- trzy wzajemnie powiązane pierścienie nazwane na cześć włoskiej rodziny renesansowej, która używała ich na herbie w XV wieku. Zauważ, że pierścienie Boromejskie nie mają dwóch połączonych pierścieni, więc jeśli odetniemy któryś z pierścieni, wszystkie trzy pierścienie się rozpadną. Niektórzy historycy spekulują, że starożytne konfiguracje pierścieni reprezentowały kiedyś trzy rodziny Visconti, Sforza i Borromeo, które utworzyły delikatny związek poprzez wewnętrzne małżeństwa. Pierścienie pojawiają się także w 1467 r. w kościele San Pancrazio we Florencji. Nawet starsze, trójkątne wersje były używane przez Wikingów, których jeden słynny przykład znaleziono na łożu wybitnej kobiety, która zmarła w 834 roku. Pierścienie pojawiają się w kontekście matematycznym w artykule z 1876 r. Na temat węzłów szkockiego fizyka matematyki Petera Taita. Ponieważ dla każdego skrzyżowania pierścienia są możliwe dwie opcje (powyżej lub poniżej), istnieje 26 = 64 możliwych wzorów z przeplotem. Jeśli weźmiemy pod uwagę symetrię, tylko 10 z tych wzorów jest geometrycznie odrębnych. Matematycy wiedzą teraz, że nie jesteśmy w stanie skonstruować prawdziwego zestawu pierścieni Boromejkich z płaskimi okręgami, i w rzeczywistości możesz to zobaczyć, jeśli utworzysz zablokowane pierścienie z drutu, co wymaga pewnego odkształcenia lub załamań w drutach . W 1987 r. Michael Freedman i Richard Skora udowodnili twierdzenie, że pierścienie Boromejskie są niemożliwe do zbudowania z płaskimi kołami. W 2004 r. Chemicy z UCLA stworzyli molekularny związek pierścieniowy Boromejski o średnicy 2,5 nanometra i zawierający sześć jonów metali. Naukowcy zastanawiają się obecnie nad sposobami wykorzystania molekularnych pierścieni Bororomejskih w tak różnorodnych dziedzinach, jak spintronika (technologia wykorzystująca spin i ładunek elektronów) oraz obrazowanie medyczne.
Mahavira (ok. 800-ok. 870)
Ganita Sara Samgraha (Kompendium esencji matematyki), datowane na 850 r., jest wyjątkowy z kilku powodów. Po pierwsze, jest to jedyny istniejący traktat o arytmetyce autorstwa uczonego Ganity. Po drugie, obejmowała zasadniczo całą wiedzę matematyczną Indii z połowy wieku. Jest to najwcześniejszy istniejący tekst indyjski poświęcony całkowicie matematyce. Ganita został napisany przez Mahavirę (lub Mahaviracharyę, co znaczy "Mahavira the Teacher"), który mieszkał w południowych Indiach. Jeden szczególny problem w książce od stuleci zachwycał uczonych i brzmiał następująco: Młoda dama kłóci się z mężem i niszczy naszyjnik. Jedna trzecia pereł naszyjnika rozprasza się na kobietę. Jedna szósta spada na łóżko. Połowa tego, co pozostało (i połowa tego, co pozostało po nim, i znowu połowa tego, co pozostało po tym, i tak dalej, licząc w sumie sześć razy) spada wszędzie. Stwierdzono, że w sumie 1161 pereł pozostaje nienaruszonych. Ile pereł dziewczynka miała pierwotnie w sumie? Zdumiewającą odpowiedzią jest to, że dziewczynka na początku miała 148 608 pereł! Zastanówmy się nad problemem. Jedna szósta spadła na łóżko. Jeden Tbird rozproszył się w jej stronę. Oznacza to, że pozostałe perły, które nie są ani na łóżku, ani w pobliżu niej, stanowią połowę wszystkich pereł. Pozostałe perły są sześciokrotnie zmniejszone o połowę, więc (1/2)7) x = 1,161, gdzie x jest całkowitą liczbą pereł; zatem x wynosi 148 608. Ogromny naszyjnik indyjskiej kobiety wart był kłótni! Ganita wyróżniała się wyraźnym stwierdzeniem, że pierwiastek kwadratowy z liczby ujemnej nie istnieje. W Canita Mahavira omówił również właściwości liczby zero i przedstawił schemat nazewnictwa dla liczb od 10 do 1024, metody uzyskiwania sumy szeregu, którego warunki są kwadratami postępu arytmetycznego, zasady określania obszaru i obwodu elipsy oraz metody rozwiązywania równań liniowych i kwadratowych.
Thabit ibn Qurra (826--901)
Pitagorejczycy starożytnej Grecji byli zafascynowani liczbami zaprzyjaźnionymi, dla których każda taka liczba jest sumą właściwych dzielników drugiej. (Właściwy dzielnik liczby nie obejmuje samej liczby.) Najmniejsza taka para to 220 i 284. Liczba 220 jest równomiernie podzielna przez 1,2,4,5,10, 11, 20, 22, 44,55 i 110, które sumują się do 284, a 284 jest równomiernie podzielne przez 1,2.4.71. oraz 142., które sumują się do 220. W 850 r. Thabit ibn Qurra, arabski astronom i matematyk, przedstawił wzór, który można wykorzystać do generowania liczb zaprzyjaźnionych. Oblicz p = 3 x 2n-1 - 1, q = 3 x 2n - 1, i r = 9 x 22n-1 - 1 dla liczby całkowitej n > 1. Jeśli p, q i r są to liczby pierwsze, to 2npq i 2nr to para liczb zaprzyjaźnionych. Gdy n = 2, daje to liczby 220 i 284, ale formuła nie generuje każdej istniejącej liczby zaprzyjażnionej. W każdym znanym przypadku liczby pary są parzyste lub oba nieparzyste. Czy kiedykolwiek odkryjemy parę zaprzyjaźnioną? Liczby zaprzyjaźnione są dość trudne do znalezienia. Na przykład do 1747 r. Leonhard Euler, szwajcarski matematyk i fizyk, znalazł tylko 30 par. Dziś wiemy o ponad 11 milionach par, ale tylko 5,001 takich par ma obie liczby mniejsze niż 3,06 x 1011.
Abu'l Hasan Ahmad ibn Ibrahim al-Uqlidisi (ok. 920-ok. 980)
'
Al-Uqlidisi ("euklidesowy") był arabskim matematykiem, którego Kitab al-fusul Ii al-hioob ai-Hindi (Rozdziały w matematyce indyjskiej) jest najwcześniej znanym dziełem arabskim omawiającym pozycyjne użycie cyfr hindusko-arabskich, co oznacza użycie cyfr odpowiadających od 0 do 9, w których każda pozycja zaczynająca się od prawej strony liczby wielocyfrowej odpowiada potędze 10 (na przykład 1, 10, 100 i 1000). Praca AI-Uqlidisi reprezentuje również najwcześniejszą znaną arytmetykę w języku arabskim. Chociaż Al-Uqlidisi urodził się i zmarł w Damaszku, dużo podróżował i mógł dowiedzieć się o hinduskiej matematyce w Indiach. Pozostała tylko jedna kopia tego rękopisu. Al-Uqlidisi omówił także problemy poprzednich matematyków w zakresie nowego systemu liczb. Dick Teresi, autor kilku książek o nauce i technologii, pisze: "Jego imię było dowodem jego czci dla Greków. Skopiował dzieła Euklidesa, stąd nazwa al-Uqlidisi. Jednym z jego dzieł jest papier i papier matematyka pióra ". W czasach al-Uqlidisi w Indiach i świecie islamskim powszechne było wykonywanie obliczeń matematycznych w piasku lub pyle, wymazując kroki w miarę postępów. Al-Uqlidisi zasugerował, aby zamiast tego używać papieru i pióra. Pisemna arytmetyka zachowuje proces i chociaż jego schemat nie obejmował usuwania liczb atramentu, pozwalał na większą elastyczność obliczeń. W pewnym sensie papier napędzał ewolucję nowoczesnych metod przeprowadzania mnożenia i dzielenia długiego. Regis Morelon, redaktor Encyklopedii Historii Nauki Arabskiej, pisze: "Jednym z najbardziej niezwykłych pomysłów w arytmetyce al-Uqlidisi jest użycie ułamków dziesiętnych" i użycie symbolu dziesiętnego. Na przykład, aby zmniejszyć o połowę 19, al-Uqlidisi podał, co następuje: 19,9,5,4.75,2.375,1.1875,0.59375. W końcu zaawansowane obliczenia dostępne w systemie dziesiętnym doprowadziły do jego powszechnego zastosowania w całym regionie i na świecie.
Omar Chajjam (1048-1131)
Omar Chajjam, perski matematyk, astronom i filozof, jest najbardziej znany ze swojej kolekcji wierszy, Rubajjata Omara Chajjama. Osiągnął jednak wielką sławę dzięki wpływowemu Traktatowi o demonstracji problemów algebry (1070). Tutaj wyprowadził metody rozwiązywania równań sześciennych i niektórych równań wyższego rzędu. Przykładem równania sześciennego, które rozwiązał, jest x3 + 200x = 20x2 + 2000. Chociaż jego podejście nie było zupełnie nowe, jego uogólnienia, które można zastosować do rozwiązania wszystkich równań sześciennych, były godne uwagi. Jego Traktat zawiera kompleksową klasyfikację równań sześciennych z rozwiązaniami geometrycznymi znalezionymi za pomocą przecinających się stożkowych odcinków. Khayyam był również w stanie pokazać, jak uzyskać n-tą potęgę dwumianową a + b w potęgach a i b, gdy n jest dowolną liczbą całkowitą. Jako tło rozważ wyrażenie (a + b)n, które jest równe (a + b) x (a + b) x (a + b) … z n powtórzeniami (a + b). Zgodnie z ekspansją dwumianową, na przykład (a + b) 5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5. Współczynniki numeryczne (1, 5, 10, 10, 5 i 1) są określane jako współczynniki dwumianowe, które są wartościami w rzędzie Trójkąta Pascala. Część prac Khayyama na ten temat faktycznie pojawia się w innej książce, do której się odwołuje, ale teraz ich utracono. Praca Khayyama na temat geometrii 1077, Sharh ma ashkala min musadarat kitab Uqlidis (Komentarze na temat trudności w postulatach Księgi Euklidesa), zapewnia ciekawe spojrzenie na słynny równoległy postulat Euklidesa. W Sharh Khayyam omawiał właściwości geometrii nieeuklidesowych i dlatego wpadł w sferę matematyki, która nie rozkwitłaby aż do 1800 roku. Dosłowne tłumaczenie imienia Chajjama to "wytwórca namiotów", możliwy handel jego ojca. Chajjam kiedyś nazywał siebie "tym, który zaszył namioty nauki".
Ibn Yahya al-Maghribi al-Samawal (ok. 1130-ok. 1180), Abu Baler ibn Muhammad ibn al Husayn al-Karaji (ok. 953-ok. 1029)
AI-Samawal (znany również jako Samau'al al-Maghribi) urodził się w Bagdadzie w rodzinie żydowskiej. Swoją pasję do matematyki zaczął rozwijać w wieku 13 lat, kiedy rozpoczął naukę od hinduskich metod obliczeniowych. W wieku 18 lat przeczytał prawie całą dostępną literaturę matematyczną, która istniała w jego czasach. AISamawal napisał swoje najsłynniejsze dzieło, al-Bahir {i'I-jabr (przetłumaczone jako The Brilliant in Algebra lub The Dazzling in Algebra), gdy miał zaledwie 19 lat. Olśniewanie jest znaczące zarówno dla jego oryginalnych pomysłów, jak i informacji dotyczących zaginionych dzieł perskiego matematyka al-Karaji z X wieku. Olśnienie podkreśla zasady arytmetyki algebry, wyjaśniając, w jaki sposób nieznane wielkości arytmetyczne lub zmienne mogą być traktowane jak zwykłe liczby, gdy rozważa się operacje arytmetyczne. AI-Samawal definiuje potęgi liczb, wielomiany i metody wyszukiwania pierwiastków wielomianów. Wielu uczonych uważa Olśniewanie za pierwszą rozprawę, która twierdzi, że x0 = I (we współczesnej notacji). Innymi słowy, al-Samawal zdał sobie sprawę i opublikował ideę, że dowolna liczba podniesiona do potęgi 0 to 1. Był również całkiem wygodny w używaniu liczb ujemnych i zera w swojej pracy, biorąc pod uwagę takie pojęcia (w nowoczesnej notacji) coś jak 0 - a = -a. Zrozumiał również, jak radzić sobie z mnożeniem przy użyciu liczb ujemnych i był dumny ze swojego odkrycia 12 + 22 + 32 + … + n2 = n (n + 1) (2n + I) / 6, co wydaje się nie występować we wcześniejszych pracach. W 1163 roku, po wielu badaniach i kontemplacji, al-Samawal przeszedł z judaizmu na islam. Nawróciłby się wcześniej w swoim życiu, ale opóźnił się, ponieważ nie chciał zranić uczuć ojca. Jego dzieło "Decydujące odrzucenie chrześcijan i Żydów" przetrwało do dziś
W 2005 roku czytelnicy, redaktorzy i panel ekspertów Forbes.com umieścili abakus jako drugie najważniejsze narzędzie wszechczasów pod względem wpływu na ludzką cywilizację. (Pierwszy i trzeci na liście to odpowiednio nóż i kompas.) Nowoczesny liczydło z koralikami i drutami, używane do liczenia, ma swoje korzenie w starożytnych urządzeniach, takich jak tabliczka Salamis, najstarsza zachowana tablica licząca używana przez Babilończycy około 300 r.p.n.e. Deski te były zwykle drewniane, metalowe lub kamienne i zawierały linie lub rowki, wzdłuż których poruszano koraliki lub kamienie. Około 1000 r.n.e. Aztekowie wymyślili nepohualtzitzin (określany przez miłośników mianem "komputera Azteków"), urządzenie przypominające liczydło, które wykorzystywało ziarna kukurydzy przewleczone przez drewniane ramki, aby pomóc operatorom wykonywać obliczenia. Liczydło, jakie znamy dzisiaj, które zawiera koraliki poruszające się wzdłuż drutów, zostało użyte w 1200 r. n.e. W Japonii liczydło nazywa się soroban. W pewnym sensie liczydło można uważać za przodka komputera i podobnie jak komputer, liczydło służy jako narzędzie umożliwiające ludziom szybkie obliczenia w handlu i inżynierii. Abakusy są nadal używane w Chinach, Japonii, częściach Związku Radzieckiego i Afryki, a czasami przez osoby niewidome, z niewielkimi różnicami w designie. Chociaż liczydło jest zwykle używane do szybkich operacji dodawania i odejmowania, doświadczeni użytkownicy mogą szybko pomnożyć, podzielić i obliczyć pierwiastki kwadratowe. W 1946 r. W Tokio w konkursie obliczeń prędkości rywalizował japoński operator Soroban z osobą używającą kalkulatora elektrycznego z tamtych czasów. Operator soroban zwykle pokonuje kalkulator elektryczny
Leonardo z Pizy (znany również jako Fibonacci, ok. 1175-ok. 1250)
Carl Boyer nazywa Leonarda z Pizy, znanego również jako Fibonacciego, "bez wątpienia najbardziej oryginalnym i najzdolniejszym matematykiem średniowiecznego świata chrześcijańskiego". Fibonacci, bogaty włoski kupiec, podróżował przez Egipt, Syrię i Barbary (Algieria), a w 1202 opublikował książkę Liber Abaci (Księga Abakusa), która wprowadziła cyfry hindusko-arabskie i system liczb dziesiętnych do Europy Zachodniej. Ten system jest obecnie używany na całym świecie, po przezwyciężeniu strasznie nieporęcznych cyfr rzymskich powszechnych w czasach Fibonacciego. W Liber Abaci, Fibonacci zauważa: "Oto dziewięć cyfr hinduski: 9 8 7 6 5 4 3 2 1. Z tymi dziewięcioma cyframi i ze znakiem 0, który w języku arabskim nazywa się: wphirum, dowolna liczba może być reprezentowane, jak zostanie wykazane. " Chociaż Liber Abaci nie był pierwszą książką europejską opisującą cyfry hindusko-arabskie - i chociaż cyfry dziesiętne nie zyskały szerokiego zastosowania w Europie bezpośrednio po jej opublikowaniu - uważa się, że książka miała silny wpływ na europejską tl, dlatego powinna był skierowany zarówno do naukowców, jak i biznesmenów. Liber Abaci wprowadził także Europę Zachodnią do słynnej sekwencji liczb 1, 1,2, 3, 5, 8, 13. .., który dziś nazywa się sekwencją Fibonacciego. Zauważ, że oprócz pierwszych dwóch liczb, każda kolejna liczba w sekwencji jest równa sumie dwóch poprzednich liczb. Liczby te pojawiają się w zadziwiającej liczbie dyscyplin matematycznych i w naturze. Czy Bóg jest matematykiem? Z pewnością wszechświat wydaje się być niezawodnie rozumiany za pomocą matematyki. Natura to matematyka. Układ nasion w słoneczniku można zrozumieć za pomocą liczb Fibonacciego. Główki słonecznika, podobnie jak inne kwiaty, zawierają rodziny splecionych spirali ziaren - jedna spirala nawija się zgodnie z ruchem wskazówek zegara, druga przeciwnie do ruchu wskazówek zegara. Liczba spiral w takich głowach, a także liczba płatków w kwiatach. jest bardzo często liczbą Fibonacciego.
Abu-I 'Abbas Ahmad ibn Khallikau (1211-1282), Dante Alighieri (1265-1321)
Problem szachownicy Sissy jest zauważalny w historii matematyki, ponieważ od stuleci jest używany do zademonstrowania natury geometrycznego wzrostu lub postępów geometrycznych i jest jednym z najwcześniejszych wzmianek o szachach w łamigłówkach. Arabski uczony Ibn Khallikan w 1256 r. wydaje się być pierwszym autorem, który omawia historię wielkiego wezyra Sissy ben Dahira, który zgodnie z legendą został zapytany przez króla Indii Shirhama, jakiej nagrody chciał wymyślić za grę w szachy. Sissa zwróciła się do króla: "Majestat, byłbym szczęśliwy, gdybyś dał mi ziarno pszenicy do umieszczenia na pierwszym kwadracie szachownicy i dwa ziarna pszenicy do umieszczenia na drugim kwadracie oraz cztery ziarna pszenicy do umieść na trzecim, a osiem ziaren pszenicy na czwartym, i tak dalej na sześćdziesiąt cztery kwadraty. " "A czy to wszystko, czego chcesz, Sissa, głupcze?" zdumiony krzyczał King. Król nie zdawał sobie sprawy, ile ziaren otrzyma Sissa Jednym ze sposobów ustalenia rozwiązania jest obliczenie sumy pierwszych 64 warunków postępu geometrycznego, 1+ 2 + 22 + ... + 263 = 264 - 1, do dawało 18,446,744,073,709 551 615 ziaren pszenicy. Możliwe, że pewna wersja tej historii była znana Dantemu, ponieważ nawiązał do podobnej koncepcji w Paradiso, aby opisać obfitość świateł Nieba: "Było ich tak wiele, że ich liczba gromadzi się szybciej niż podwojenie szachownicy". Lan Gullberg pisze: "Przy około 100 ziarnach na centymetr sześcienny całkowita objętość pszenicy [Sissy] wynosiłaby prawie ... dwieście kilometrów sześciennych, które zostałyby załadowane na dwa tysiące milionów wagonów kolejowych, co stanowiłoby pociąg dojeżdżający tysiąc razy wokół Ziemi. "
Nicole Oresme (1323-1382), Pietro Mengoli (1626-1686), Johann Bernoulli (1667-1748), Jacob Bernoulli (1654-1705)
Gdyby Bóg był nieskończonością, wówczas rozbieżnymi seriami byłyby Jego anioły latające coraz wyżej, aby do Niego dotrzeć. PRZEZ wieczność wszystkie takie anioły zbliżają się do swojego Stwórcy. Rozważmy na przykład następujące nieskończone szeregi: 1 + 2 + 3 + 4 … Jeśli dodamy jeden termin serii co roku, za cztery lata suma wyniesie 10. W końcu, po nieskończonej liczbie lata suma osiąga nieskończoność. Matematycy nazywają takie szeregi rozbieżnymi, ponieważ eksplodują w nieskończoność, biorąc pod uwagę nieskończoną liczbę terminów. W tym wpisie interesuje nas seria, która różni się znacznie wolniej. Interesuje nas bardziej magiczna seria, być może anioł ze słabszymi skrzydłami. Rozważmy szereg harmoniczny, pierwszy znany przykład rozbieżnej serii, której warunki zbliżają się do zera: 1 + 1/2 + 1/3 + 1/4 + … Oczywiście ta seria eksploduje wolniej niż nasz poprzedni przykład, ale wciąż rośnie do nieskończoności. W rzeczywistości rośnie tak niesamowicie powoli, że jeśli dodamy termin w ciągu roku
, za 1043 lata mielibyśmy sumę mniejszą niż 100. William Dunham pisze, Doświadczeni matematycy zapominają, jak zaskakujące jest to zjawisko dla niewtajemniczonego studenta - że , dodając coraz bardziej nieistotne terminy, osiągamy jednak sumę większą niż jakakolwiek wcześniej ustalona ilość. "Nicole Oresme, słynny francuski filozof średniowiecza, jako pierwszy udowodnił rozbieżność szeregów harmonicznych (ok. 1350). wyniki zostały utracone przez kilka stuleci, a wynik udowodnił agam włoski matematyk Pietro Mengoh w 1647 r. i szwajcarski matematyk Johann Bernoulli w 1687 r. Jego brat Jacob Bernoulli opublikował dowód w swojej pracy z 1689 Tractatus de Seriebus Infinitis (Traktat o nieskończonej serii) , który zamyka: "A więc dusza bezmiaru mieszka w minutach. A w najwęższych granicach nie ma żadnych ograniczeń. Cóż za radość rozpoznawać minutę w nieskończoności! Ogromny do dostrzeżenia w małej, jaka boskość!
Ghiyath ai-Din Jamshid Mas'ud al-Kashi (ok. 1380-1429), Francois Viete (1540-1603)
Prawo cosinusów można wykorzystać do obliczenia długości jednego boku trójkąta, gdy znany jest kąt przeciwny do tego boku oraz długość pozostałych dwóch boków. Prawo może być wyrażone jako c2 = a2 + b2 - 2abcos (C), gdzie a, b i c są długościami boków trójkąta, a C jest kątem między bokami a i b. Ze względu na swoją ogólność stosowanie prawa rozciąga się od geodezji lądowej do obliczania wysokości ścieżek samolotów. Zauważ, jak prawo cosinusa staje się twierdzeniem Pitagorasa (c2 = a22 + b2) dla trójkątów prostokątnych, gdy C staje się 90°, a cosinus staje się zerowy. Zauważ też, że jeśli znane są wszystkie trzy długości boków trójkąta, możemy użyć prawa cosinusów do obliczenia kątów trójkąta. Elementy Euklidesa (ok. 300 p.n.e.) zawierają ziarna pojęć, które prowadzą do prawa cosinusów. W XV wieku perski astronom i matematyk al-Kashi przedstawił dokładne tabele trygonometryczne i wyraził twierdzenie w formie odpowiedniej do współczesnego
użycia. Francuski matematyk Francois Viete odkrył prawo niezależnie od al-Kashi. Po francusku prawo cosinusa nosi nazwę Theoreme d'Al-Kashi, po ujednoliceniu istniejących dzieł na ten temat przez al-Kashiego. Najważniejszą pracą Al-Kashiego jest ukończony w 1427 r. Klucz do arytmetyki, który omawia matematykę wykorzystywaną w astronomii, geodezji, architekturze i rachunkowości. Al-Kashi używa ułamków dziesiętnych do obliczania całkowitego pola powierzchni potrzebnego dla niektórych muqamów, struktur dekoracyjnych w architekturze islamskiej i perskiej. Viete prowadziła fascynujące życie. W pewnym momencie z powodzeniem złamał kody Filipa II Hiszpanii dla Henryka IV Francji. Filip wierzył, że bardzo skomplikowany szyfr nie może zostać złamany przez zwykłych ludzi, a kiedy odkrył, że Francuzi znają jego plany wojskowe, poskarżył się papieżowi, że czarną magię stosuje się przeciwko jego krajowi.
Europejskie teksty arytmetyczne z XV i XVI wieku często przedstawiały matematyczne problemy słowne związane z handlem w celu nauczania pojęć matematycznych. Ogólna koncepcja problemów słownych dla uczniów sięga wieków, a niektóre z najstarszych znanych problemów słownych były prezentowane w starożytnym Egipcie, Chinach i Indiach. Treviso Arithmetic jest pełen problemów słownych, wielu angażuje kupców inwestujących pieniądze i którzy chcą uniknąć oszustwa. Książka została napisana w weneckim dialekcie i opublikowana w 1478 roku w miejscowości Treviso we Włoszech. Nieznany autor książki pisze: "Często młodzi ludzie, którymi się interesuję, i którzy z niecierpliwością czekają na kupieckie zajęcia, często proszą mnie o napisanie podstawowych zasad arytmetyki. im, a według wartości przedmiotu, mam najlepszą z moich małych zdolności podjętych w celu ich zaspokojenia w pewnym stopniu ". Następnie daje liczne problemy słowne z udziałem kupców o nazwiskach takich jak Sebastiano i Jacomo, którzy inwestują swoje pieniądze w celu uzyskania partnerstwa. Książka pokazuje także kilka sposobów przeprowadzania mnożenia i zawiera informacje z pracy Fibonacciego Liber Abaci (1202). Treviso ma szczególne znaczenie, ponieważ jest to pierwsza znana drukowana książka matematyczna w Europie. Promował także użycie hinduskiego systemu liczbowego i algorytmów obliczeniowych. Ponieważ ówczesny handel zaczął mieć szeroki komponent międzynarodowy, potencjalni biznesmeni musieli pilnie zająć się matematyką. Dziś uczeni są zafascynowani Treviso, ponieważ stanowi portal z metodami nauczania matematyki w piętnastowiecznej Europie. Podobnie, ponieważ problemy obejmują obliczanie płatności za wymianę towarów, cięcie tkanin, handel szafranem, mieszanki stopów w monetach, wymianę walut i obliczanie udziałów w zyskach pochodzących ze współpracy, czytelnicy rozumieją współczesne obawy dotyczące oszustwa, lichwy i ustalanie opłat odsetkowych.
Gottfried Wilhelm Leibniz (1646-1716), James Gregory (1638--1675), Nilakantha Somayaji (1444-1544)
Szereg nieskończony jest sumą nieskończenie wielu liczb i odgrywa ważną rolę w matematyce. W przypadku serii takich jak 1 + 2 + 3 + … suma jest nieskończona i mówi się, że szereg się różni. Szereg naprzemienny to taki, w którym co drugi termin jest ujemny. Jedna szczególna seria na przemian intrygowała matematyków od stuleci. Pi, symbolizowane grecką literą π, jest stosunkiem obwodu koła do jego średnicy i może być wyrażone za pomocą niezwykle prostej formuły: π/ 4 = 1 - 1/3 + 1/5 - 1/7+… Zauważ również, że funkcję arctan w trygonometrii można wyrazić za pomocą arctan (x)= - x/3 + x/5 - x/7 + … Korzystając z serii arctan, serię dla π / 4 uzyskuje się przez ustawienie x = 1. Ranjan Roy zauważa, że niezależne odkrycie nieskończonego szeregu dla π przez różne osoby żyjące w różnych środowiskach i kulturach daje nam wgląd w charakter matematyki jako dyscyplina uniwersalna . Cykl został odkryty przez niemieckiego matematyka Gottfrieda Wilhelma Leibniza, szkockiego matematyka i
astronoma Jamesa Gregory′ego oraz indyjskiego matematyka z XIV lub XV wieku, którego tożsamość nie jest ostatecznie znana, chociaż wynik zwykle przypisuje się Nilakantha Somayaji. Leibniz odkrył formułę w 1673 r., a Gregory odkrył ją w 1671 r. Roy pisze: "Odkrycie nieskończonego szerego Leibniza dla π było pierwszym największym osiągnięciem Leibniza". Holenderski matematyk Christiaan Huygens powiedział Leibnizowi, że ta niezwykła właściwość koła będzie świętowana wśród matematyków na zawsze. Nawet Newton powiedział, że formuła ujawniła geniusz Leibniza. Odkrycie Gregory′ego dotyczące formuły arctan nastąpiło przed Leibniza, chociaż Gregory nie zauważył specjalnego przypadku formuły arctan dla π/4. Ta nieskończona seria Arctan została również podana w 1500 książce Somayaji Tantrasangraha. Somayaji zdawał sobie sprawę, że skończona seria liczb wymiernych nigdy nie wystarcza do przedstawienia π.
Ojciec Luca Bartolomeo de Pacioli (1445-1517)
W 1509 roku włoski matematyk Luca Pacioli, bliski przyjaciel Leonarda da Vinci, opublikował Divina Proportione, rozprawę na temat numeru znanego obecnie jako "Złoty stosunek". Ten stosunek, symbolizowany przez fil, pojawia się z niesamowitą częstotliwością w matematyce i przyrodzie. Możemy najłatwiej zrozumieć proporcję, dzieląc linię na dwa segmenty, tak aby stosunek całego segmentu do dłuższej części był taki sam jak stosunek dłuższej części do krótszej części lub (a + b)/b = b/a = 1,61803… Jeśli długości boków prostokąta są w złotym stosunku, wówczas prostokąt jest "złotym prostokątem". Można podzielić złoty prostokąt na kwadrat i złoty prostokąt. Następnie możemy wyciąć mniejszy złoty prostokąt na mniejszy kwadrat i złoty prostokąt. Możemy kontynuować ten proces w nieskończoność, wytwarzając coraz mniejsze złote prostokąty. Jeśli narysujemy przekątną z górnego prawego rogu oryginalnego prostokąta w lewym dolnym rogu, a następnie z dolnego prawego rogu niemowlęcia (czyli następnego mniejszego)
złotego prostokąta w lewym górnym rogu, punkt przecięcia pokaże punkt, w którym wszystkie złote prostokąty dziecka zbiegają się. Ponadto długości przekątnych są w złotym stosunku do siebie. Punkt, w którym zbiegają się wszystkie złote prostokąty, jest czasem nazywany "okiem Boga". Złoty prostokąt jest jedynym prostokątem, z którego można wyciąć kwadrat, dzięki czemu pozostały prostokąt będzie zawsze podobny do oryginalnego prostokąta. Jeśli połączymy wierzchołki na diagramie, przybliżymy spiralę logarytmiczną, która "otacza" Oko Boga. Spirale logarytmiczne są wszędzie - muszle morskie, rogi zwierząt, ślimak ucha - wszędzie tam, gdzie przyroda musi wypełniać przestrzeń w sposób ekonomiczny i regularny. Spirala jest mocna i zużywa minimum materiałów. Podczas rozbudowy. zmienia swój rozmiar, ale nigdy nie ma kształtu.
Johannes Trithemius (1462-1516), Abu Yusuf Yaqub ibn Ishaq al-Sabbah AI-Kindi (ok. 801-873)
Dzisiaj teoria matematyki stała się kluczowa dla kryptografii. Jednak w czasach starożytnych często stosowano proste szyfry zastępcze, w których litery w wiadomości zastępowano innymi literami. Na przykład CAT staje się DBU, zastępując każdą literę w CAT literą następującą po nim w alfabecie Oczywiście takie proste szyfry stały się łatwe do złamania po odkryciu analizy częstotliwości, na przykład, przez arabskiego uczonego al-Kindiego w dziewiątym stulecie. Ta metoda analizuje, które litery występują najczęściej w języku - takim jak ETAOIN SHRDLU w języku angielskim - i wykorzystuje te informacje do rozwiązywania kodów zastępczych. Można stosować bardziej złożone statystyki, takie jak uwzględnianie liczby par listów. Na przykład Q prawie zawsze występuje razem z U w języku angielskim. Pierwsza drukowana książka o kryptografii, Polygraphiae Libri Sex (Six Books of Polygraphy), została napisana przez niemieckiego opata Johannesa Trithemiusa i opublikowana w 1518 roku, po jego śmierci. Polygraphiae zawiera setki kolumn łacińskich słów, ułożonych w dwóch kolumnach na stronie. Każde słowo oznacza literę alfabetu. Na przykład pierwsza strona zaczyna się tak:
a: Deus
b: Stwórca
c: Gonditor
a: Clemens
b: clementissimus
c: pius
Aby zakodować wiadomość, używa się słowa oznaczającego literę. Co ciekawe, Trithemius skonstruował tablice, tak że zakodowany fragment wydaje się mieć sens jako rzeczywista modlitwa. Na przykład, jeśli dwie pierwsze litery w orędziu brzmią CA, modlitwa rozpoczyna się od Clemens Conditor (Miłosierny Stwórca) jako pierwszych dwóch słów w zdaniu łacińskim. Pozostałe książki Polygraphiae przedstawiają bardziej wyrafinowane metody kryptograficzne wraz z tabelami do kreatywnego ukrywania informacji. Inne słynne dzieło Trithemiusa, Steganographia (napisane w 1499 r. I opublikowane w 1606 r.), Zostało umieszczone na "Liście książek zakazanych" Kościoła Katolickiego, ponieważ wydawało się, że jest to książka o czarnej magii, ale w rzeczywistości była to tylko kolejna książka z kodami!
Pedro Nunes (1502-1578)
Do celów nawigacji naziemnej spirala loksodromowa - znana również jako spirala sferyczna, loksodrom lub linia loksodromy - przechodzi przez południki północ-południe Ziemi pod stałym kątem. Loxodrome cewki jak gigantyczny wąż wokół Ziemi i spirale wokół biegunów, nie docierając do nich. Jednym ze sposobów żeglowania po Ziemi jest próba pokonywania najkrótszej ścieżki między punktami, która biegnie wzdłuż łuku wielkiego koła wokół Ziemi. Jednak pomimo tego, że jest to najkrótsza ścieżka, nawigator musi stale dostosowywać kurs w oparciu o odczyty kompasu, co jest prawie niemożliwym zadaniem dla pierwszych nawigatorów. Z drugiej strony ścieżka loksodromiczna umożliwia nawigatorowi ciągłe kierowanie statku do tego samego punktu kompasu, nawet jeśli ścieżka do miejsca docelowego jest dłuższa. Na przykład, korzystając z tego podejścia do podróży z Nowego Jorku do Londynu, podróżnik może skierować się na stałą pozycję wynoszącą 73° na wschód od północy. Lokoksodrom jest reprezentowany jako linia prosta na mapie projekcji Mercatora. Lokoksodrom został wymyślony przez portugalskiego matematyka i geografa Pedro Nunesa. Nunes żył w czasach, gdy inkwizycja wywołała strach w sercu Europy. Wielu Żydów w Hiszpanii przymusowo nawrócono na katolicyzm, a Nunes nawrócił się jako dziecko. Głównymi celami późniejszej inkwizycji hiszpańskiej byli potomkowie tych konwersacji, tacy jak wnukowie Nunesa na początku 1600 roku. Gerardus Mercator (1512-1594), flamandzki kartograf, został uwięziony przez Inkwizycję z powodu jego protestanckiej wiary i szerokich podróży, a on ledwo uniknął egzekucji. Niektóre grupy muzułmańskie w Ameryce Północnej wykorzystują linię loksodromu do Mekki (południowy wschód) jako swoją qibla (kierunek modlitwy) zamiast korzystać z tradycyjnej najkrótszej ścieżki. W 2006 r. Malezyjska Narodowa Agencja Kosmiczna (MYNASA) sponsorowała konferencję mającą na celu określenie właściwej qibli dla muzułmanów na orbicie.
Gerolamo Cardano (1501-1576), Niccolo Tartaglia (1500-1557), Lodovico Ferrari (1522-1565)
Włoski renesansowy matematyk, lekarz, astrolog i hazardzista Gerolamo Cardano jest najbardziej znany ze swojej pracy nad algebrą zwaną Artis magnae, sive de regulis algebraicis (Of the Great Art lub The Rules of Algebra) - zwaną również zwięźlejszą nazwą Ars magna. Chociaż książka dobrze się sprzedawała, zauważa Jan Gullberg: "Żadna pojedyncza publikacja nie promuje zainteresowania algebrą, jak Ars magna Cardano, która jednak zapewnia bardzo nudne czytanie współczesnemu peruserowi poprzez konsekwentne poświęcanie stron pełnej retoryki rozwiązaniu .. .. Przy niestrudzonej branży młynka do organów Cardano monotonnie powtarza to samo rozwiązanie dla kilkunastu lub więcej prawie identycznych problemów, w których wystarczyłby tylko jeden. " Niemniej imponująca praca Cardano ujawniła rozwiązania różnych rodzajów równań sześciennych i kwartalnych - to znaczy równań ze zmiennymi podniesionymi odpowiednio do trzeciej i czwartej potęgi. Włoski matematyk Niccolo Tartaglia wcześniej poinformował Cardano o rozwiązaniu
sześciennym, x3 + ax = b, i próbował upewnić się, że Cardano nigdy nie opublikuje rozwiązania, zmuszając Cardano do złożenia przysięgi na Boga. Cardano i tak opublikował to rozwiązanie, po tym, jak wydawało mu się, że Tartaglia nie był pierwszym, który rozwiązał równanie sześcienne za pomocą rodników. Ogólne równanie kwartowe rozwiązał uczeń Cardano, Lodovico Ferrari. W Ars magna Cardano badał istnienie tak zwanych liczb urojonych, które są oparte na pierwiastku kwadratowym z \, chociaż nie w pełni docenił ich właściwości. W rzeczywistości pierwsze obliczenia przedstawia liczbami zespolonymi, pisząc: "Odrzucając psychiczne tortury i mnożąc 5 + √5 przez 5 - √5, otrzymujemy 25 - (- 15). Zatem iloczyn wynosi 40" W 1570 r. w wyniku inkwizycji Cardano został wtrącony do więzienia na kilka miesięcy pod zarzutem herezji, ponieważ stworzył horoskop Jezusa Chrystusa. Według legendy Cardano poprawnie zobrazował dokładną datę swojej śmierci, jak mówi przepowiednia, zabijając się w tym dniu.
Juan Diez (1480--1549)
Sumario compendioso, opublikowane w Mexico City w 1556 roku, jest pierwszym dziełem na temat matematyki wydrukowanym w obu Amerykach. Publikacja Sumario compendioso w Nowym Świecie poprzedza wiele dekad emigracji purytanów do Ameryki Północnej i osady w Jamestown w stanie Wirginia. Autor, brat Juan Diez, był towarzyszem hiszpańskiego konkwistadora Hernando Cortesa podczas podbojów Cortesa przez imperium Azteków. Diez napisał książkę przede wszystkim dla osób kupujących złoto i srebro odzyskane z kopalni Peru i Meksyku. Oprócz dostarczania tabel ułatwiających handlowcom uzyskiwanie wartości liczbowych bez większych obliczeń, poświęcił także część pracy algebrze związanej z równaniem kwadratowym - to znaczy równaniami w postaci ax2 + bx + c = 0 z a ≠ O. Na przykład jeden z problemów można przetłumaczyć jako: "Znajdź kwadrat, od którego odejmuje się 15 ? …, wynikiem jest jego własny pierwiastek." Jest to równoważne rozwiązaniu x2 -15 ? = x . Pełny tytuł pracy Dieza brzmi: Sumario compendioso de las quentas de plata y oro que in los reynos del Pim son mustarios a los mercaderes y todo genera de Iratantes los algunos reglos tocantes al Arithmetica, co przekłada się na "Kompleksowe podsumowanie liczenia srebra i Złoto, które w Królestwach Peru są niezbędne dla kupców i wszelkiego rodzaju handlowców. Prasa drukarska i papier zostały wysłane z Hiszpanii, a następnie przewiezione do Mexico City". Obecnie istnieją tylko cztery znane kopie Sumario compendioso. Według Shirley Gray i C. Edwarda Sandifera: "Pierwsza książka z matematyki w języku angielskim na świecie została wydana dopiero w 1703 roku ... Ze wszystkich kolonialnych książek z matematyki, te w języku hiszpańskim są najciekawsze, ponieważ w większości zostały napisane Ameryka do użytku przez ludzi mieszkających w Ameryce. "
Gerardus Mercator (1512-1594), Edward Wright (ok. 1558-1615)
Wiele starożytnych greckich pomysłów na przedstawianie kulistej Ziemi na płaskiej mapie zostało utraconych w średniowieczu. John Short wyjaśnia, że w XV wieku "wartość map morskich rywalizowała ze złotem jako głównym celem kapitanów korsarzy. Później mapy stały się symbolami statusu wśród bogatych kupców, którzy budowali ogromne fortuny dzięki kwitnącym szlakom handlowym umożliwianym przez niezawodną nawigację morską . " Jedną z najbardziej znanych projekcji map w historii jest mapa Mercator (1569), która stała się powszechnie używana w żegludze i nosi imię flamandzkiego kartografa Gerardusa Mercatora. Norman Thrower pisze: "Podobnie jak kilka innych rzutów, Mercator jest konformalny (kształty wokół punktu są prawidłowe), ale ma także unikalną właściwość: linie proste są loksodromami lub loksodromami (linie o stałym namiocie kompasu)". Ta ostatnia jakość była nieoceniona dla żeglarzy morskich, którzy wybrali trasy za pomocą kompasów i innych urządzeń, aby wskazać kierunki geograficzne i sterować statkami. Korzystanie z mapy Mercator wzrosło w 1700 roku, po wynalezieniu dokładnego morskiego chronometru, urządzenia do pomiaru czasu używanego do określania długości geograficznej za pomocą nawigacji niebieskiej. Chociaż Mercator był pierwszym twórcą map, który stworzył swoją projekcję, w której linie kompasu przecinają południki pod stałym, określonym kątem, prawdopodobnie zastosował metody graficzne i małą matematykę. Angielski matematyk Edward Wright przedstawił analizę fascynujących właściwości mapy w swoim "Pewnym". Błędy w nawigacji (1599). W przypadku czytnika pochylonego matematycznie odwzorowanie mapy Mercatora o współrzędnych x i y można utworzyć na podstawie wartości szerokości φ długości geograficznej przez λ x = λ - λ0 i y= sinh-1(tan(φ)), gdzie λ0 długością geograficzną w centrum mapy. Projekcja Mercatora ma swoje niedoskonałości; na przykład przesadza rozmiar obszarów daleko od równika
Rafael Bombelli (1526-1572)
Liczba urojona to liczba, której kwadrat ma wartość ujemną. Wielki matematyk Gottfried Leibniz nazwał liczby urojone "cudownym / światłem Ducha Bożego; są prawie płazem między bytem a nieistnieniem". Ponieważ kwadrat dowolnej liczby rzeczywistej jest dodatni, przez stulecia wielu matematyków deklarowało, że liczba ujemna nie ma pierwiastka kwadratowego. Chociaż różni matematycy mieli wyobrażenie o liczbach urojonych, historia liczb wyobrażonych zaczęła kwitnąć w XVI-wiecznej Europie. Włoski inżynier Rafael Bombelli, znany za swojego czasu osuszając bagna, jest dziś znany ze swojej Algebry, opublikowanej 10 1572, która wprowadziła notację √-1, która byłaby poprawnym rozwiązaniem równania x2 + 1 = 0. Napisał: "To była szalona myśl w ocenie wielu . " Wielu matematyków wahało się "uwierzyć" w liczby urojone, w tym Kartezjusz, który tak naprawdę wprowadził pojęcie imaginacji jako rodzaj zniewagi. Leonhard Euler w XVIII wieku wprowadził symbol i dla √ -1 dla pierwszej litery łacińskiego słowa imaginarius - i nadal używamy dzisiaj symbolu Eulera. Kluczowe postępy we współczesnej fizyce nie byłyby możliwe bez użycia liczb urojonych, które pomogły fizykom w szerokim zakresie obliczeń, w tym w wydajnych obliczeniach z wykorzystaniem prądów przemiennych, teorii względności. przetwarzanie sygnałów, dynamika luid i mechanika kwantowa. Wyimaginowane liczby odgrywają nawet rolę w produkcji wspaniałych dzieł fraktalnych, które pokazują bogactwo szczegółów wraz ze wzrostem powiększenia. Od teorii strun do teorii kwantów, im głębiej studiuje się fizykę, tym bardziej zbliża się do czystej matematyki. Niektórzy mogą nawet powiedzieć, że matematyka "uruchamia" rzeczywistość w taki sam sposób, jak system operacyjny Microsoft działa na komputerze. Równanie falowe Schrodingera - które opisuje podstawową rzeczywistość i zdarzenia w kategoriach funkcji falowych i prawdopodobieństw - można uznać za zanikające podłoże, na którym wszyscy istniejemy, i opiera się na liczbach urojonych.
Johannes Kepler (1571-1630), Thomas Callister Hales (1740-1780)
Wyobraź sobie, że Twoim celem jest wypełnienie dużego pudełka jak największą liczbą piłek golfowych. Po zakończeniu szczelnie zamknij pokrywę. Gęstość kulek jest określana na podstawie proporcji objętości pudełka zawierającego piłkę. Aby wsunąć jak najwięcej piłek do pudełka, musisz odkryć układ o największej możliwej gęstości. Jeśli po prostu upuścisz kulki do pudełka, osiągniesz gęstość około 65 procent. Jeśli jesteś ostrożny i utwórz warstwę na dole w układzie sześciokątnym, a następnie umieść następną warstwę kulek we wgłębieniach utworzonych przez dolną warstwę i kontynuuj, będziesz w stanie osiągnąć gęstość upakowania wynoszącą &π/8, co stanowi około 74 procent. W 1611 roku niemiecki matematyk i astronom Johannes Kepler napisał, że żaden inny układ kulek nie ma wyższej średniej gęstości. W szczególności w swojej monografii The Six-Comered Snowflake doszedł do wniosku, że niemożliwe jest spakowanie identycznych kulek w trzech wymiarach większych niż wypełnienie znalezione w sześciokątnym wypełnieniu skierowanym do twarzy. W dziewiętnastym wieku Karl Friedrich Gauss udowodnił, że tradycyjny układ heksagonalny był najbardziej wydajny dla zwykłej siatki 3-D. Niemniej jednak hipoteza Keplera pozostała, a było pewne, czy można uzyskać gęstsze upakowanie przy nieregularnym wypełnieniu. Wreszcie w 1998 r amerykański matematyk Thomas Hales oszołomił świat, gdy przedstawił dowód, że Kepler miał rację. Równanie Halesa i jego 150 zmiennych wyrażały każdy możliwy układ 50 sfer. Komputery potwierdziły, że żadna kombinacja zmiennych nie doprowadziła do wydajności pakowania wyższej niż 74 procent. Annals of Mathematics zgodziły się opublikować dowód, pod warunkiem, że został zaakceptowany przez panel 12 sędziów. W 2003 r. Panel stwierdził, że byli "w 99 procentach pewni" co do poprawności dowodu. Hales ocenia, że przygotowanie pełnego formalnego dowodu zajmie około 20 lat pracy.
John Napier (1550-1617)
Szkocki matematyk John Napier jest znany jako wynalazca i promotor logarytmów w swojej książce z 1614 r. "Opis reguły logarytmicznej Marvela". Od tego czasu metoda ta przyczyniła się do niezliczonych postępów w nauce i inżynierii, umożliwiając trudne obliczenia. Zanim kalkulatory elektroniczne stały się powszechnie dostępne, logarytmy i tabele logarytmów były powszechnie używane w pomiarach i nawigacji. Napier był także wynalazcą kości Napiera, prętów rzeźbionych przy pomocy tabliczek mnożenia, które można było układać we wzory, aby pomóc w obliczeniach. Logarytm (a o podstawie b) liczby x jest wyrażany jako logb(x) i równa się wykładowi, który spełnia x = by. Na przykład, ponieważ 35 = 3 x 3 x 3 x 3 x 3 = 243, mówimy, że log 243 (o podstawie 3) to 5 lub logl3(243) = 5. Jako inny przykład, log10(100) = 2 Dla celów praktycznych należy wziąć pod uwagę, że mnożenie, takie jak 8 x 16 = 128, może zostać przepisane jako 23 x 24 = 27, przekształcając w ten sposób obliczenia w te uwzględniające proste dodawanie mocy (3 + 4 = 7). Przed kalkulatorami, w celu pomnożenia dwóch liczb, inżynier często sprawdzał logarytmy obu liczb w tabeli, dodawał je, a następnie sprawdzał wynik w tabeli, aby znaleźć produkt. Często może to być szybsze niż pomnożenie ręczne i jest to zasada, na której oparte są reguły slajdów. Dzisiaj różne wielkości i skale w nauce są wyrażane jako logarytmy innych wielkości. Na przykład skala pH w chemii, belkowa jednostka miary w akustyce i skala Richtera stosowana do pomiaru intensywności trzęsień ziemi obejmują skalę logarytmiczną 10. Co ciekawe, odkrycie logarytmów tuż przed erą Izaaka Newtona miało wpływ na naukę porównywalny z wynalezieniem komputera w XX wieku.
William Oughtred (1574-1660)
Ci z was, którzy chodzili do liceum przed latami 70. XX wieku, mogą pamiętać, że zasada suwaka wydawała się kiedyś tak powszechna jak maszyna do pisania. W ciągu kilku sekund inżynierowie mogą mnożyć, dzielić, znajdować pierwiastki kwadratowe i robić wiele więcej. Najwcześniejsza wersja z przesuwanymi elementami została wynaleziona w 1621 roku przez angielskiego matematyka i anglikańskiego ministra Williama Oughtreda, w oparciu o logarytmy szkockiego matematyka Johna Napiera. Oughtred mógł początkowo nie docenić wartości swojej pracy, ponieważ nie opublikował szybko swoich ustaleń. Według niektórych relacji, jeden z jego uczniów ukradł ten pomysł i opublikował broszurę na temat zasady slajdów, która podkreślała jego przenośność i zachwycił się tym, że urządzenie "nadaje się do użytku na koniu jak na głupcu". Oughtred oburzył się na dwulicowość jego ucznia. W 1850 r. 19-letni francuski porucznik artylerii zmodyfikował oryginalny projekt suwaka, a armia francuska wykorzystała go do obliczeń pocisków podczas walki z Prusami. Podczas II wojny światowej amerykańskie bombowce często stosowały wyspecjalizowane reguły ślizgowe. Cliff Stoll, guru od suwaków, pisze: "Zastanów się nad osiągnięciami inżynieryjnymi, które zawdzięczają ich istnieniu poprzez połączenie dwóch kijów: Empire State Building; Hoover Dam; zakręty Golden Gate Bridge; hydrodynamiczne transmisje samochodowe, tranzystory radiowe; Boeing 707 samolot pasażerski. " Wernher Von Braun, projektant niemieckiej rakiety V-2, podobnie jak Albert Einstein, polegał na regułach ślizgowych niemieckiej firmy Nestler. Reguły slajdów Picketta znajdowały się na pokładzie misji kosmicznych Apollo na wypadek awarii komputerów W XX wieku na całym świecie wyprodukowano 40 milionów reguł slajdów. Biorąc pod uwagę kluczową rolę tego urządzenia od rewolucji przemysłowej do czasów współczesnych, urządzenie zasługuje na miejsce w tej książce. Literatura z Oughtred Society stwierdza: "Przez okres 3,5 stuleci był używany do obliczeń projektowych dla praktycznie wszystkich głównych budowli zbudowanych na tej ziemi".
Pierre de Fermat (1601-1665), Rene Descartes (1596 - 1650)
Na początku 16 roku życia Pierre de Fermat, francuski prawnik i matematyk, dokonał genialnych odkryć w teorii liczb i innych dziedzinach matematyki. Jego rękopis z 1636 r. "Ad locos pIanos et solidos Iisagoge" ("Wprowadzenie do płaszczyzny i bryły Loci") wykroczył poza prace Rene Descartesa w geometrii analitycznej i pozwolił Fermatowi zdefiniować i zbadać wiele ważnych krzywych, w tym cykloidę i spiralę Fermata. Spirala Fermata lub spirala paraboliczna może być utworzona za pomocą równania biegunowego, r2 = a2θ. W tym przypadku r jest odległością krzywej od początku, a jest stałą, która określa, jak ciasno nawinięta jest spirala, a θ jest kątem biegunowym. Dla każdej dodatniej wartości θ ujemne i dodatnie wartości r istnieją, które prowadzą do krzywej symetrycznej względem początku. Fermat badał zależność obszaru zamkniętego ramieniem spirali i osi x podczas obrotu spirali. Dzisiaj specjaliści od grafiki komputerowej czasami używają tej krzywej do modelowania rozmieszczenia główek nasion w kwiatach. Na przykład możemy narysować plamy, które mają pozycje środkowe określone przez wartości współrzędnych biegunowych, r(i) = ki-2/2, i kąty θ zdefiniowane przez θ(i) = 2iπ/τ. Tutaj τ jest złotą liczbą (1+√5)/2, a i jest po prostu licznikiem, który kroczy jako), 2,3,4, .., To podejście graficzne wytwarza wiele różnych ramion spiralnych, które skręcają się w jednym kierunku lub inny Możliwe jest prześledzenie różnych zestawów symetrycznych spiral, promieniujących od środka wzoru, na przykład zestaw 8, 13 lub 21 ramion spiralnych, a wszystkie te liczby ramion są liczbami Fibonacciego (patrz wpis Liber Abaci Fibonacciego). Michael Mahoney pisze: "Fermat pracował przez pewien czas ze spiralami, zanim spotkał go w Dialogach Galie;eusza. W liście z 3 czerwca 1636 r. Opisał spiralę Mersenne′ r2 = a2θ…"
Pierre de Fermat (1601-1665), Andrew John Wiles (ur. 1953), Johann Dirichlet (1805-1859), Gabriel Lame (1795-1870)
Na początku XVI wieku francuski prawnik Pierre de Fermat dokonał genialnych odkryć w teorii liczb. Chociaż był matematykiem "amatorskim", stworzył matematyczne wyzwania, takie jak Last Theorem Fermata (FLT), który został rozwiązany dopiero w 1994 roku przez brytyjsko-amerykańskiego matematyka Andrew Wilesa. Wiles spędził siedem lat swojego życia, próbując udowodnić słynne twierdzenie, które mogło wygenerować więcej prób udowodnienia niż jakiekolwiek inne twierdzenie. FLT stwierdza, że xn + yn = zn, "nie ma niezerowych rozwiązań liczb całkowitych dla x, y i z, gdy n > 2." Fermat stwierdził swoje twierdzenie w 1637 roku, kiedy napisał w swojej kopii Arytmetyki Diofantusa:" … ma naprawdę cudowny dowód na tę propozycję,na którą ten margines jest zbyt wąski, aby ją pomieścić" .Dziś uważamy, że Fermat nie miał takiego dowodu. Fermat nie był zwykłym prawnikiem. Uważany jest wraz z Blaise Pascal (1623-1662) za założyciel teorii prawdopodobieństwa. Jako współtwórca geometrii analitycznej wraz z Rene Descartes (1596-1650) uważany jest za jednego z pierwszych współczesnych matematyków. Kiedyś zastanawiał się, czy można znaleźć odpowiedni trójkąt, którego przeciwprostokątna i sumy nóg były kwadratami. Dziś wiemy, że najmniejsze trzy liczby spełniające te warunki są dość duże: 45 655 566,027,761, 1 061 652 293,520 i 4 677 298 610 289. Od czasów Fermata FLT zaowocował znaczącymi badaniami matematycznymi i zupełnie nowymi metodami. W 1832 r. Johann Dirichlet opublikował dowód Ostatnie twierdzenie Ferrnata dla n=14. Gabriel Lame udowodnił to dla n = 7 w 1839 r. Amir Aczel pisze, że FLT "stałoby się najbardziej zagadkową matematyczną tajemnicą na świecie. Proste, eleganckie i [pozornie] całkowicie niemożliwe do udowodnienia, ostatnie twierdzenie Fermata pobudziło wyobraźnię amatorów i zawodowych matematyków przez ponad trzy stulecia. Dla niektórych stała się cudowną pasją. Dla innych była to obsesja, która doprowadziła do oszustwa, intrygi lub szaleństwa ".
Rene Descartes (1596-1650)
W 1637 r. Francuski filozof i matematyk Rene Descartes opublikował La geometrie, która pokazuje, w jaki sposób geometryczne kształty i liczby można analizować za pomocą algebry. Praca Kartezjusza wpłynęła na ewolucję geometrii analitycznej, dziedziny matematyki obejmującej reprezentację pozycji w układzie współrzędnych, w której matematycy analizują algebraicznie takie pozycje. La geometrie pokazuje także, jak rozwiązywać problemy matematyczne i omawia reprezentację punktów płaszczyzny za pomocą liczb rzeczywistych oraz reprezentację i klasyfikację krzywych za pomocą równań. Co ciekawe, La geometria w rzeczywistości nie używa osi współrzędnych "kartezjańskich" ani żadnego innego układu współrzędnych. Książka zwraca tyle samo uwagi na reprezentowanie algebry w formach geometrycznych, co na odwrót. Kartezjusz uważał, że algebraiczne kroki w dowodzie powinny zwykle odpowiadają reprezentacji geometrycznej. Jan Gullberg pisze: "La geometrie to najwcześniejszy tekst matematyczny współczesny , student matematyki potrafił czytać bez potknięcia się o mnóstwo przestarzałych notacji … Wraz z Principią Newtona jest to jeden z najbardziej wpływowych tekstów naukowych XVII wieku. "Według Carla Boyera Descartes pragnął" uwolnić geometrię "od użycia diagramów poprzez procedury 1algebraiczne i nadać sens działaniom algebry poprzez interpretacja geometryczna. Mówiąc bardziej ogólnie, Kartezjusz dokonał przełomu w swojej propozycji połączenia algebry i geometrii w jeden temat, jak pisze Judith Grabiner: "Tak jak historia zachodniej filozofii była postrzegana jako seria przypisów do Platona, tak przez ostatnie 350 lat matematyka może być postrzegana jako seria przypisów do geometrii Kartezjusza … i triumfu metod rozwiązywania problemów przez Kartezjusza. "Boyer konkluduje:" Pod względem zdolności matematycznych Kartezjusz prawdopodobnie był najbardziej. zdolny myśliciel swoich czasów, ale tak naprawdę nie był matematykiem. "Jego geometria była tylko jeden aspekt pełnego życia, który obracał się wokół nauki, filozofii i religii.
Albrecht Durer (1471-1528), Etienne Pascal (1588-1640), Ole Romer (1644-1710), Philippe de La Hire (1640-1718), Johann Castillon (1704-1791)
Kardioid w kształcie serca od stuleci fascynuje matematyków swoimi matematycznymi właściwościami, pięknem graficznym i praktycznymi zastosowaniami. Krzywa może być wytworzona po prostu przez śledzenie punktu na kole, który toczy się po innym (stałym) kole o tym samym promieniu. Nazwa pochodzi od greckiego słowa oznaczającego serce, a jej równanie biegunowe można zapisać jako r = a (1 - cosθ). Obszar kardioidy wynosi (3/2)πa2, a jego obwód wynosi 8a. Kardioida może być również generowana przez narysowanie okręgu C i ustalenie na nim punktu P. Następnie narysuj zestaw różnych kół wyśrodkowanych na obwodzie C i mijającym Przez P. Kręgi te kształtują kardioidalny kształt. Kardioid pojawia się w wielu pozornie odmiennych obszarach matematycznych, od kaustyki w dziedzinie optyki do centralnego kształtu zestawu Mandelbrota w geometrii fraktalnej. Wiele dat może być związanych z kardioidem. Francuski prawnik i matematyk amator Etienne Pascal, ojciec matematyka Blaise Pascal, formalnie
przestudiował bardziej ogólny przypadek tej krzywej. nazywa się Limacon z Pascala 1637. Jednak nawet wcześniej niemiecki malarz i matematyk Albrecht Diirer przedstawił melodię do rysowania Limy w Underweysung der Meßung (Instruction In Measurement), opublikowanym w 1525 r. W 1674 r. Duński astronom Ole Rjilmer rozważał kardioidę, rozważając kształty teelh biegów. Francuski malematyk Philippe de La Hire określił swoją lenglh w 1708 roku. Co ciekawe, kardioida otrzymała swoją sugestywną nazwę dopiero w 1741 roku, kiedy Johann Castillon nazwał ją w swoim traktacie o transakcjach filozoficznych Towarzystwa Królewskiego. Glen Vecchione wyjaśnia praktyczną stronę kardioidów, gdy pisze, że mogą wykazać wzorce interferencji i zgodności fal, które promieniują koncentrycznie ze źródła punktowego. W ten sposób mogą zidentyfikować obszary o największej czułości na mikrofonach lub antenach. … Mikrofon kardioidalny jest wrażliwy na dźwięk z przodu i minimalizuje dźwięk z tyłu.
Rene Descartes (1596-1650) ,Jacob Bernoulli (1654-1705)
Spirale logarytmiczne w naturze są wszechobecne i mają szereg przejawów botanicznych i zoologicznych. Prawdopodobnie najczęstszymi przykładami są logarytmiczne spirale muszli łodzika i innych muszli morskich. rogi różnych ssaków. układ nasion wielu roślin (takich jak słonecznik i stokrotka). i łuski szyszki. Martin Cardner zauważył, że Eperia. popularna odmiana pająka. obraca sieć, w której pasmo cewki wokół centrum w spirali logarytmicznej Spirala logarytmiczna (znana również jako spirala równokątna lub spirala Bernoulliego) może być wyrażona jako r= keaθ. gdzie T jest odległością od początku. Kąt 0 między linią styczną do krzywej a linią promieniową narysowaną na (r, θ) jest stała. Spirala została po raz pierwszy omówiona przez francuskiego matematyka i filozofa Rene Descartesa w 1638 r. W listach napisanych do francuskiego teologa i matematyka Marina Mersenne. spirala została dokładniej zbadana przez szwajcarskiego matematyka Jacoba Bernoulli. Najbardziej imponujący wygląd spirali logarytmicznej znajduje się w ogromnych ramionach wielu galaktyk, a tradycyjny pogląd polega na tym, że konieczne jest oddziaływanie dalekiego zasięgu, takie jak grawitacja, aby stworzyć tak ogromne porządek. W galaktykach spiralnych ramiona spiralne są miejscami aktywnego formowania się gwiazd. Wzory spiralne często pojawiają się spontanicznie w materii zorganizowanej przez transformacje symetryczne: zmiana wielkości (wzrostu) a obrót. Forma podąża za funkcją. a forma spiralna może umożliwiać zagęszczanie na stosunkowo dużej długości. Długie, ale kompaktowe rurki są przydatne z mięczaków i ślimaków z oczywistych powodów. w tym wytrzymałość fizyczna i zwiększona powierzchnia. Jako członek gatunku dorasta. ogólnie przekształca się w taki sposób, że jego części zachowują w przybliżeniu ten sam stosunek względem siebie. i jest to prawdopodobnie powód, dla którego natura często wykazuje podobny wzrost spirali.
Leon Battista Alberti (1404-1472), Gerard Desargues (1591-1661), Jean-Victor Poncelet (1788-1867)
Geometria rzutowa ogólnie dotyczy relacji między kształtami i ich odwzorowaniami lub "obrazami", które wynikają z rzutowania kształtów na powierzchnię. Rzuty mogą być często wizualizowane jako cienie rzucane przez obiekty. Włoski architekt Leon Battista Alberti był jedną z pierwszych osób, które eksperymentowały z geometrią rzutową poprzez swoje zainteresowanie perspektywą w sztuce. Mówiąc bardziej ogólnie, renesansowi artyści i architekci zajmowali się metodami przedstawiania trójwymiarowych obiektów na dwuwymiarowych rysunkach. Alberti czasami umieszczał szklany ekran między sobą a krajobrazem, zamykał jedno oko i zaznaczał na szkle pewne punkty, które wyglądały jak na obrazie. Wynikowy rysunek 2D dał wierne wrażenie sceny 3D. Francuski matematyk Gerard Oesargues był pierwszym profesjonalnym matematykiem, który sformalizował geometrię rzutową, szukając sposobów na rozszerzenie geometrii euklidesowej. W 1636 r. Desargues opublikowało Exemple de l'une des mani, res universelles du S.G.D.L. touchant la
pratique de la perspective (Przykład metody uniwersalnej autorstwa Sieur Girarda Desargues Lyonnais dotyczący praktyki perspektywy), w której przedstawił geometryczną metodę konstruowania perspektywicznych obrazów obiektów. W projekcie Desargues zbadano także właściwości kształtów, które zostały zachowane w ramach odwzorowań perspektywicznych. Malarze i rytownicy wykorzystali jego podejście. Najważniejsze dzieło Desargues, Brouillon proiect d'une lonte aux evenements des rencontres d'un cone avec un plan (Szorstki projekt osiągnięcia efektu przecięcia stożka z płaszczyzną), opublikowane w 1639 r., Traktuje teorię przekrojów stożkowych przy użyciu geometria rzutowa. W 1882 r. Francuski matematyk i inżynier Jean-Victor Poncelet (1788-1867) opublikował traktat, który ożywił zainteresowanie geometrią rzutową. W geometrii rzutowej elementy takie jak punkty, linie i płaszczyzny zwykle pozostają punktami, liniami i płaszczyznami podczas rzutowania. Jednak długości, stosunki długości i kąty mogą się zmieniać podczas projekcji. W geometrii rzutowej równoległe linie w geometrii euklidesowej przecinają się w nieskończoności w rzucie.
'
Evangelista Torricelli (1608-1647)
Twój przyjaciel podaje ci galon czerwonej farby i pyta, jak całkowicie pomalować nieskończoną powierzchnię za pomocą tego galona farby. Jaką powierzchnię byś wybrał? Istnieje wiele możliwych odpowiedzi na to pytanie, ale trąbka Torricellego jest jednym znanym kształtem do rozważenia - przypominający róg obiekt utworzony przez obrót f(x) = 1/x dla x ∈ [1, ∞ ] wokół osi x. Można użyć standardowych metod rachunku różniczkowego aby wykazać, że trąbka Torricellego ma skończoną objętość, ale nieskończoną powierzchnię! John dePillis wyjaśnia, że matematycznie wlanie czerwonej farby do trąbki Torricellego może napełnić lejek, a tym samym można pomalować całe wnętrze nieliniową powierzchnią, nawet jeśli ty mają linitową liczbę cząsteczek farby. Ten pozorny paradoks można częściowo rozwiązać, pamiętając, że trąbka Torricellego jest w rzeczywistości konstrukcją matematyczną, a nasza skończona liczba cząsteczek farby, która "wypełnia" róg, jest przybliżeniem rzeczywistej skończonej objętości rogu. Dla jakich wartości a f(x) = 1/xa produkuje róg o skończonej objętości i nieskończonej powierzchni? To jest coś, co możesz przemyśleć z matematycznymi przyjaciółmi. Trąbka Torricellego nazywany jest czasem rogiem Gabriela i nosi imię włoskiego fizyka i matematyka Evangelisty Torricellego, który odkrył go w 1641 roku. Był zaskoczony tą trąbką, która wydawała się nieskończenie długą bryłą o nieskończonej powierzchni i skończonej objętości. Torricelli i jego koledzy uważali, że to głęboki paradoks i niestety nie mieli narzędzi rachunku różniczkowego, aby w pełni docenić i zrozumieć przedmiot. Dziś Torricelli jest pamiętany z astronomii teleskopowej zrobił to z Galileo i za jego wynalazek barometru. Nazwa "róg Gabriela" przywołuje wizje Archanioła Gabriela, dmuchającego w róg, aby ogłosić Dzień Sądu, łącząc w ten sposób nieskończoność z mocami Boga
Blaise Pascal (1623-1662), Omar Chajjam (1048-1131)
Jednym z najbardziej znanych wzorców liczb całkowitych w historii matematyki jest trójkąt Pascala. Blaise Pascal był pierwszym, który napisał traktat o tym postępie w 1654 r., Chociaż wzór ten znany był perskiemu poecie i matematykowi Omarowi Chajjamowi już w AD 1100, a nawet wcześniej matematykom z Indii i starożytnych Chin. Pierwsze siedem rzędów trójkąta Pascala przedstawiono w prawym górnym rogu. Każda liczba w trójkącie jest sumą dwóch powyżej. Matematycy omawiali rolę, jaką trójkąt Pascala odgrywa w teorii prawdopodobieństwa, w ekspansji dwumianów formy (x + y)n oraz w różnych zastosowaniach teorii liczb od lat. Matematyk Donald Knuth (ur. 1938) wskazał kiedyś, że istnieją tak wiele relacji i wzorców w trójkącie Pascala, że kiedy ktoś odkrywa nową tożsamość, nie ma już wielu ludzi, którzy się tym ekscytują, z wyjątkiem odkrywcy. Niemniej fascynujące badania ujawniły niezliczone cuda, w tym specjalne wzory geometryczne na przekątnych, istnienie idealnych kwadratowych wzorów o różnych właściwościach heksagonalnych oraz rozszerzenie trójkąta i jego wzorów na ujemne liczby całkowite i na wyższe wymiary. Gdy liczby parzyste w trójkącie zostaną zastąpione kropkami, a liczby nieparzyste przerwami, powstały wzór będzie fraktalem , ze złożonymi powtarzającymi się wzorami w różnych skalach wielkości. Te ligatury fraktalne mogą mieć praktyczne znaczenie, ponieważ mogą zapewnić modele dla naukowcy pomagają w tworzeniu nowych struktur o nowatorskich właściwościach. Na przykład w J 986 naukowcy stworzyli uszczelki druciane w skali wielkości mikrona prawie identyczne z trójkątem Pascala, z otworami na liczby nieparzyste. Powierzchnia ich najmniejszego trójkąta wynosiła około 1,38 mikrona do kwadratu, a naukowcy zbadali wiele niezwykłych właściwości ich nadprzewodzącej uszczelki w polu magnetycznym
William Neile (1637-1670), John Wallis (1616-1703)
W 1657 r. Brytyjski matematyk William Neile stał się pierwszą osobą, która "wyprostowała" lub znalazła długość łuku nietrywialnej krzywej algebraicznej. Ta specjalna krzywa jest nazywana parabolą półksiężycową, zdefiniowaną przez x3 = ay2. Zapisany jako y = ±ax3/2, łatwiej jest zobaczyć, jak można go uznać za "pół sześcienny", a stąd geneza terminu semicubic. Raport z pracy Neile'a pojawił się w D Cycloide brytyjskiego matematyka Johna Wallisa w 1659 r. Co ciekawe, jedynie długości łuku krzywych transcendentalnych, takich jak spirala logarytmiczna i cykloida, zostały obliczone przed 1659 r. Ponieważ próby naprawy elipsy i hiperboli zakończyły się niepowodzeniem , niektórzy matematycy, tacy jak francuski filozof i matematyk Rene Descartes (1596-1650), przypuszczali, że niewiele krzywych można naprawić. Jednak włoski fizyk i matematyk Evangelista TorricelIi (1608--1647) wyprostował spiralę logarytmiczną, która była pierwszą zakrzywioną linią (inną niż okrąg), której długość została określona. Cykloid był następną krzywą rektyfikowaną przez angielskiego geometra i architekta Sir Christopher Wren (1632-1723) w 1658 r. Około 1687 r. Holenderski matematyk i fizyk Christiaan Huygens (1629-1695) wykazał, że parabola półksiężycowa jest krzywą, wzdłuż której cząstka może opadać pod wpływem siły grawitacji, dzięki czemu porusza się w równych odległościach pionowych w równych czasach. Półprzewodnikowa parabola może być również wyrażona jako para równań: x = t2 i y = at3. Biorąc pod uwagę tę postać, długość krzywej w funkcji to (1/27) x (4 + 9 t2)3/23 = ax t2, która umieszcza wierzchołek krzywej skierowany w dół wzdłuż osi y zamiast w lewo na osi x.
Vincenzo Viviani (1622-1703)
Umieść punkt w trójkącie równobocznym. Od tego miejsca narysuj linię po każdej stronie, aby te trzy linie były prostopadłe do każdej strony. Bez względu na to, gdzie umieścisz punkt, suma odległości prostopadłych od punktu do boków jest równa wysokości trójkąta. Twierdzenie to nosi imię włoskiego matematyka i naukowca Vincenzo Viviani. Galileusz był pod takim wrażeniem talentu Viviani, że zabrał go do swojego domu w Arcetri we Włoszech, jako współpracownika. Badacze znaleźli sposoby rozszerzenia twierdzenia Vivianiego na problemy, w których punkt znajduje się poza trójkątem, a także zbadali zastosowanie tego twierdzenia do dowolnego regularnego wielokąta n-stronnego. W tym przypadku suma prostopadłych odległości od punktu wewnętrznego do n boków jest n-krotnością apotemu wielokąta. (Apothem to odległość od środka do boku.) Twierdzenie to można również badać w większych wymiarach. Po śmierci Galileusza Viviani napisała biografię Galileusza i miał nadzieję opublikować pełne wydanie dzieł Galileusza. Niestety, Kościół zabronił tego wysiłku, który zaszkodził reputacji Viviani i był ciosem dla nauki w ogóle. Viviani opublikował włoską wersję Elementów Euklidesa w 1690 roku. Twierdzenie to jest nie tylko interesujące matematycznie ze względu na wiele różnych dowodów, twierdzenie to służy do nauczania dzieciom różnych aspektów geometrii. Niektórzy nauczyciele umieścili problem w realnym świecie, rzucając go w kontekście surfera, który utknął na wyspie w kształcie trójkąta równobocznego. Surferka chce zbudować chatę, w której suma odległości do boków jest minimalna, ponieważ surfuje po każdej z trzech plaż w jednakowym czasie. Uczniowie są bardzo zadowoleni z tego, że umieszczenie chaty nie ma znaczenia..
Isaac Newton (1642-1727), Gottfried Wilhelm Leibniz (1646--1716)
Angielski matematyk Isaac Newton i niemiecki matematyk Gottfried Wilhelm Leibniz zwykle przypisuje się wynalezienie rachunku różniczkowego, ale różni wcześniejsi matematycy badali pojęcie stawek i limitów. zaczynając od starożytnych Egipcjan, którzy opracowali zasady obliczania objętości piramid i przybliżania obszarów kręgów. W XVI wieku zarówno Newton, jak i Leibniz zastanawiali się nad problemami stycznych, szybkości zmian, minimów, maksimów i nieskończenie małych (niewyobrażalnie małe ilości, które są prawie, ale nie całkiem zerowe). Obaj mężczyźni zrozumieli, że różnicowanie (znajdowanie stycznej do krzywej w punkcie - to znaczy linia prosta, która "dotyka" krzywej w tym punkcie) i całkowanie (znajdowanie obszaru pod krzywą) są procesami odwrotnymi. Odkrycie Newtona (1665-1666) rozpoczęło się od jego zainteresowania nieskończonymi kwotami; jednak bardzo wolno publikował swoje odkrycia. Leibniz opublikował swoje odkrycie rachunku różniczkowego w 1684 r. I rachunku całkowego w 1686 r. Powiedział: "Niegodni doskonałych ludzi, tracić godziny jak niewolnicy w obliczeniach
Mój nowy rachunek
oferuje prawdę rodzaj analizy i bez wysiłku wyobraźni. " Newton był oburzony. Przez wiele lat toczyły się debaty na temat podziału uznania za odkrycie rachunku różniczkowego, w wyniku czego postęp w rachunku różnił się. Newton jako pierwszy zastosował rachunek różniczkowy do problemów w fizyce, a Leibniz opracował znaczną część zapisu znanego z współczesnych rachunków różniczkowych. Dzisiaj rachunek różniczkowy i inwazyjny opanował każdą dziedzinę badań naukowych i odgrywa nieocenioną rolę w biologii, fizyce, chemii, ekonomii, socjologii i inżynierii oraz w każdej dziedzinie, w której zmienia się pewna ilość, na przykład prędkość lub temperatura. Rachunku można użyć do wyjaśnienia struktury tęczy, nauczenia nas, jak zarabiać więcej na giełdzie, kierować statkiem kosmicznym, prognozować pogodę, przewidywać wzrost populacji, projektować budynki i analizować rozprzestrzenianie się chorób. Rachunek spowodował rewolucję. Zmieniło to nasze spojrzenie na świat.
Isaac Newton (1642-1727)
Wykorzystanie technik obliczeniowych opartych na relacjach powtarzalności, w których każdy termin sekwencji jest zdefiniowany jako funkcja poprzedniego terminu, można prześledzić od początku matematyki. Babilończycy zastosowali takie techniki do obliczenia pierwiastka kwadratowego liczby dodatniej, a Grecy do przybliżenia liczby pi. Obecnie wiele ważnych specjalnych funkcji fizyki matematycznej można obliczyć za pomocą wzorów rekurencyjnych. Analiza numeryczna często dotyczy uzyskania przybliżonych rozwiązań trudnych problemów. Metoda Newtona jest jedną z najbardziej znanych metod numerycznych rozwiązywania równań formy f{x)=0, których niektóre rozwiązania mogą być trudne do znalezienia przy użyciu prostych metod algebraicznych. Problem znajdowania zer lub pierwiastków funkcji za pomocą tego rodzaju metod występuje często w nauce i inżynierii. Aby zastosować metodę Newtona, zaczynamy od numerycznego odgadnięcia rozwiązania pierwiastka, a następnie funkcja jest aproksymowana przez jej linię styczną, która jest linią prostą, która "dotyka" wykresu funkcji w jednym punkcie. Po określeniu przecięcia x tej linii, które jest często lepszym przybliżeniem pobliskiego pierwiastka niż początkowe przypuszczenie, metodę można powtórzyć (powtórzyć), aby uzyskać kolejno dokładne przybliżenia. Dokładna formuła metody Newtona to xn+1 = xn - f(xn) / f′(xn), gdzie symbol (′) wskazuje pierwszą pochodną funkcji f Gdy metoda jest stosowana do funkcji o złożonych wartościach, komputer Wersje graficzne są czasami używane w celu wskazania, gdzie można polegać na metodzie i gdzie zachowuje się dziwnie. Powstała grafika często ujawnia chaotyczne zachowanie i piękne fraktalne wzory. Ziarna matematyczne dla metody Newtona zostały opisane przez Izaaka Newtona w De analysi per aequationes numero terminorum infinitas (O analizie przez równania z nieskończoną liczbą terminów), napisane w 1669 r. I opublikowane przez Williama Jonesa w 1711. W 1740 r. Brytyjski matematyk Thomas Simpson udoskonalił to podejście i opisał metodę Newtona jako iteracyjną metodę rozwiązywania ogólnych równań nieliniowych za pomocą rachunku różniczkowego.
Christiaan Huygens (1629-1695)
W XVI wieku matematycy i fizycy szukali krzywej, która określa kształt specjalnego rodzaju rampy. W szczególności obiekty umieszczane są na rampie, pojedynczo, i muszą ześlizgnąć się na sam dół, zawsze w tym samym czasie i bez względu na to, gdzie zaczynają się na rampie. Obiekty są przyspieszane przez grawitację i uważa się, że rampa nie ma tarcia. Holenderski matematyk, astronom i fizyk Christiaan Huygens odkrył rozwiązanie w 1673 roku i opublikował je w swoim Horologium oscillatoriumi (The Pendulum Clock). Technicznie rzecz biorąc, tautochron jest cykloidalny - to znaczy krzywą określoną przez ścieżkę punktu na krawędzi koła, gdy koło toczy się po linii prostej. Tautochron jest również nazywany brachistochronem w odniesieniu do krzywej, która daje obiektowi pozbawionemu tarcia najszybszą prędkość opadania, gdy obiekt zsuwa się z jednego pomta na drugi. Huygens próbował wykorzystać swoje odkrycie do zaprojektowania dokładniejszego zegara wahadłowego. Zegar wykorzystywał fragmenty powierzchni tautochronu w pobliżu miejsca, w którym sznurek obracał się, aby zapewnić, że sznurek podąża za optymalną krzywą, niezależnie od tego, gdzie wahadło zaczęło się kołysać. (Niestety, tarcie spowodowane powierzchniami spowodowało poważne błędy.) Moby Dick wspomniał o specjalnej właściwości tautochronu w dyskusji na temat próbnika, miski używanej do wytłaczania tłuszczu do produkcji oleju: "[Próbnik ] jest także miejscem do głębokiej medytacji matematycznej. To właśnie w lewostronnym naczyniu Pequod, z kamienistą pieczołowitością krążącą wokół mnie, najpierw zostałem pośrednio uderzony niezwykłym działaniem, że w geometrii wszystkie ciała ślizgają się wzdłuż na przykład cykloid, mój kamień steatytowy, zejdzie z dowolnego miejsca w tym samym czasie "
Ole Christensen Romer (1644-1710)
Astroid to krzywa z czterema guzkami, która jest wyznaczona przez punkt na kole, który toczy się jak koło zębate wzdłuż wnętrza większego koła. Ten większy okrąg ma czterokrotność średnicy małego koła. Astroid wyróżnia się różnorodnością znanych matematyków, którzy badali jego intrygujące właściwości. Krzywą tę po raz pierwszy zbadał duński astronom Ole Romer w 1674 r., W wyniku poszukiwań zębów przekładni o bardziej przydatnych kształtach. Szwajcarski matematyk Johann Bernoulli (1691), niemiecki matematyk Gottfried Leibniz (1715) i francuski matematyk Jean d'Alembert (1748) zafascynowali się krzywą. Astroid ma równanie x2/3 + y2/3 = R2/3, gdzie R jest promieniem stacjonarnego koła zewnętrznego, a R/4 jest promieniem wewnętrznego koła tocznego. Długość astroida wynosi 6R, a pole to 3πR2/8. Co ciekawe, jego obwód 6R nie jest zależny od π, pomimo zaangażowania kół, które są wykorzystywane do generowania astroidu. W 1725 r. Matematyk Daniel Bernoulli odkrył, że astroid jest również śledzony przez wewnętrzny okrąg, który ma średnicę stałego koła. Innymi słowy, wykrywa to tę samą krzywą, co wewnętrzny okrąg z tylko y … średnicą większego. W fizyce krzywa astroida Stonera-Wohlfartha jest używana do scharakteryzowania różnych właściwości energii i magnetyzmu. USA Patent 4,987,984 opisuje zastosowanie astroidv w mechanicznych sprzęgłach rolkowych: "Krzywa astroidów zapewnia takie samo dobre rozproszenie naprężeń, jak w przypadku równoważnego łuku kołowego, chata usuwa mniej materiału bieżni krzywki, dając mocniejszą strukturę". Co ciekawe, linie styczne wzdłuż krzywej astroidu, gdy są przedłużane, aż dotkną osi X i Y, wszystkie mają tę samą długość. Możesz to sobie wyobrazić, wyobrażając sobie drabinę opierając się pod wszystkimi możliwymi kątami o ścianę, co wykrywa część krzywej astroidu.
Guillaume Francois Antoine, markiz de l′Hopital (1661-1704)
W 1696 r. Francuski matematyk markiz de l′Hopital opublikował pierwszy w Europie podręcznik rachunku różniczkowego, Analyze des infiniment petit., Pour I'intelligence des lignes courbes (Analiza nieskończenie małego, dla zrozumienia krzywych). Chciał, aby książka była narzędziem promującym zrozumienie technik rachunku różniczkowego. Rachunek został wynaleziony kilka lat wcześniej przez Izaaka Newtona i Gottfrieda Leibniza i udoskonalony przez braci Bernoulli, matematyków Jacoba i Johanna. Keith Devlin pisze: "W rzeczywistości, do czasu pojawienia się książki Humala, Newton, Leibniz i dwaj Bernoullowie byli całkiem nieźle jedynymi ludźmi na powierzchni ziemi, którzy wiedzieli wiele o rachunku różniczkowym". Na początku lat 90. XIX wieku I'Hopital zatrudnił Johanna Bernoulli'ego, aby uczył go rachunku różniczkowego. L'Hopital był tak zaintrygowany rachunkiem różniczkowym, że szybko się nauczył i wkrótce skonsolidował swoją wiedzę w swoim obszernym podręczniku. Rouse Ball pisze o książce l′Hopital:
"zasługa stworzenia pierwszego traktatu wyjaśniającego zasady i zastosowanie metody wynika z l′Hopital…" Praca ta miała szeroki obieg; wprowadziła notację różnicową do ogólnego używać we Francji i pomógł rozpowszechnić go w Europie ". Oprócz swojego podręcznika I'Hopital jest znany z zawartej w jego książce zasady rachunku różniczkowego, służącej do obliczania wartości granicznej ułamka, którego licznik i mianownik zbliżają się do zera lub oba zbliżają się do nieskończoności. Początkowo planował karierę wojskową, ale słaby wzrok spowodował, że przeszedł na matematykę. Dziś wiemy, że I'Hopital w 1694 r. Płacił Bernoulliemu 300 franków rocznie, aby opowiedzieć mu o swoich odkryciach, które opisałem w swojej książce. W 1704 roku, po śmierci I'Hopital, Bernoulli zaczął mówić o umowie i twierdził, że wiele wyników w Analizy nieskończenie małego było dzięki niemu".
William Whiston (1667-1752)
Chociaż ta łamigłówka nie jest kamieniem milowym na równi z większością innych , ten mały klejnot z 1702 r. jest godny uwagi, ponieważ intrygował uczniów i dorosłych od ponad dwóch stuleci i jest metaforą tego, jak prosta matematyka może pomagają analitykom rozumować poza granicami własnej intuicji. Wyobraź sobie, że masz linę, która ściśle otacza równik koszykówki. Jak długo trzeba by zrobić linę, aby we wszystkich punktach znajdowała się jedna stopa od powierzchni koszykówki? Jak zgadujesz Następnie wyobraź sobie, że mamy linę wokół równika kuli wielkości Ziemi, co daje długość liny około 25 000 mil! Jak długo musiałbyś teraz robić linę, aby znajdowała się jedną stopę nad ziemią wokół równika? Odpowiedź, która jest zaskoczeniem dla większości ludzi, to 2π lub około 6,28 stopy zarówno dla koszykówki, jak i dla Ziemi, tylko o długości dorosłego mężczyzny. Jeśli R jest promieniem Ziemi, a 1 + R jest promieniem, w stopach, powiększonego koła, możemy porównać obwód liny przed (2πR) i po 2π(1 + R), co pokazuje różnica wynosi 2 stopy IT, niezależnie od promienia Ziemi lub koszykówki. Układanka bardzo podobna do tej pojawiła się w książce Williama Whistona The Elements of Euclid, napisanej w 1702 roku dla studentów. Whiston - angielski teolog, historyk i matematyk - był prawdopodobnie najbardziej znany ze swojej A New Theory of the Earth from its Original to the Consummation of All Things (1696), w której sugeruje, że powódź Noego był spowodowany przez kometę.
Jacob Bernoulli (1654-1705)
W 1713 r. Szwajcarski matematyk Jacob Bernoulli udowodnił swoje prawo wielkich liczb (LLN) w pośmiertnej publikacji Ars Coniectandi (The Art of Conieeluring). LLN jest twierdzeniem prawdopodobieństwa, które opisuje długoterminową stabilność zmiennej losowej. Na przykład, gdy liczba obserwacji eksperymentu (takich jak rzucanie monetą) jest wystarczająco duża, wówczas proporcja wyniku (np. Występowanie głów) będzie na przykład bliska prawdopodobieństwa wyniku, na przykład 0,5 Mówiąc bardziej formalnie, biorąc pod uwagę sekwencję niezależnych i identycznie rozmieszczonych zmiennych losowych o skończonej średniej populacji i wariancji, średnia z tych obserwacji zbliży się do teoretycznej średniej populacji. Wyobraź sobie, że rzucasz standardową sześciościenną kostką. Oczekujemy, że średnia z wartości uzyskanych przez podrzucanie będzie średnią lub 3,5. Wyobraź sobie, że pierwsze trzy rzuty mają miejsce na 1,2, i 6, dając średnią oB. Przy większej liczbie rzutów wartość średniej ostatecznie ustala się na oczekiwaną wartość 3,5. Operatorzy kasyn uwielbiają LLN, ponieważ mogą liczyć na stabilne wyniki w dłuższej perspektywie i mogą odpowiednio planować. Ubezpieczyciele polegają na LLN, aby radzić sobie i planować zmiany strat.
W Ars Coniectandi Bernoulli szacuje udział białych kulek w urnie wypełnionej nieznaną liczbą czarnych i białych kulek. Wyciągając piłki z urny i "losowo" zastępując piłkę po każdym losowaniu, ocenia proporcję białych kulek na podstawie proporcji wylosowanych piłek, które są białe. Robiąc to wystarczająco dużo razy, zyskuje dowolną pożądaną dokładność oszacowania. Bernoulli pisze: "Gdyby obserwacje wszystkich wydarzeń miały być kontynuowane przez całą wieczność (a zatem ostateczne prawdopodobieństwo zmierzałoby do doskonałej pewności), wszystko na świecie byłoby postrzegane jako zdarzające się w ustalonych proporcjach ... Nawet w najbardziej przypadkowe ... zdarzenia, z pewnością uznalibyśmy ... pewien los. "
Leonhard Paul Euler (1707-1783)
David Darling, brytyjski pisarz naukowy, pisze, że liczba e jest "prawdopodobnie najważniejszą liczbą w matematyce. Chociaż pi jest bardziej znana laikowi, e jest znacznie bardziej znacząca i wszechobecna w wyższych zakresach przedmiotu". Liczba e, która jest w przybliżeniu równa 2,71828, może być obliczona na wiele sposobów. Na przykład jest to wartość graniczna wyrażenia (I + l / n) podniesiona do n-tej potęgi, gdy n wzrasta w nieskończoność. Chociaż matematycy tacy jak Jacob Bernoulli i Gottfried Leibniz byli świadomi stałej, szwajcarski matematyk Leonhard Euler był jednym z pierwszych, którzy intensywnie przestudiowali liczbę, i jako pierwszy użył symbolu e w listach napisanych w 1727 roku. W 1737 roku wykazał, że e jest irracjonalny - to znaczy nie można go wyrazić jako stosunek dwóch liczb całkowitych. W 1748 r. Obliczył 18 cyfr, a dziś znanych jest ponad 100 000 000 000 cyfr e. e stosuje się go w różnych obszarach, takich jak wzór na łańcuchowy kształt wiszącej liny wspartej na jej dwóch końcach, do obliczania odsetek złożonych oraz w wielu zastosowaniach w prawdopodobieństwie i statystyce. Pojawia się również w jednym z najbardziej niesamowitych związków matematycznych, jakie kiedykolwiek odkryto, ff "" + I = 0, który łączy pięć najważniejszych symboli matematyki: 1,0, "11", e i i (pierwiastek kwadratowy z minus jeden). Matematyk z Harvardu, Benjamin Pierce, powiedział: "nie możemy zrozumieć [formuły] i nie wiemy, co to znaczy, ale udowodniliśmy to i dlatego wiemy, że to musi być prawda". Kilka ankiet wśród matematyków umieściło tę formułę na szczycie listy najpiękniejszych formuł w matematyce. Kasner i Newman zauważają: "Możemy tylko odtworzyć równanie i nie przestać badać jego konsekwencji. W równym stopniu przemawia do mistyków, naukowców i matematyków ".
James Stirling (1692-1770)
W dzisiejszych czasach silnie są wszędzie w matematyce. Dla nieujemnych liczb całkowitych n, "n silnia" (zapisana jako n!), jest iloczynem wszystkich liczb całkowitych dodatnich mniejszych lub równych n. Na przykład 4! = 1 x 2 x 3 x 4 = 24. Notacja n! został wprowadzony przez francuskiego matematyka Christiana Krampa w 1808 roku. Czynniki są ważne w kombinatorykach, na przykład przy określaniu liczby różnych sposobów układania obiektów w sekwencji. Występują również w teorii liczb, prawdopodobieństwie i rachunku różniczkowym. Ponieważ wartości silni rosną tak bardzo (na przykład 70! Jest większa niż 10100, a 25,206! jest większa niż 10100 000), dogodne metody przybliżania dużych silni są niezwykle przydatne. Wzór Stirlinga, n! ≈ √2πe-nnn+1/2, zapewnia dokładne oszacowanie dla n silni. Tutaj symbol ≈ oznacza "w przybliżeniu równy", zaś e i π są stałymi matematycznymi e ≈ 2,71828 a π ≈ 3,14159. W przypadku dużych wartości n wyrażenie to daje jeszcze prostsze przybliżenie, ln(n!) ≈ nln(n) - n, które można również zapisać jako n! ≈ nne-n. W 1730 r. szkocki matematyk James Stirling przedstawił swoje przybliżenie dla wartość n! w jego najważniejszym dziele, Methodus Differentialis. Stirling rozpoczął karierę w matematyce pośród konfliktów politycznych i religijnych. Przyjaźnił się z Newtonem. ale większość swojego życia po 1735 roku poświęcił zarządzaniu przemysłowemu. Keith Ball pisze: "Moim zdaniem jest to jedno z najistotniejszych odkryć matematyki XVIII -wiecznej. Taka formuła daje nam wyobrażenie o zdumiewającej transformacji matematyki, która miała miejsce w XVII i XVIII wieku. Logarytmy były wynaleziony dopiero około 1600 r. Principia Newtona, określająca zasady rachunku różniczkowego, pojawiła się 90 lat później. W ciągu kolejnych 90 lat matematycy tworzyli formuły podobne do wzoru subtelności Stirlinga, który byłby niewyobrażalny bez sformalizowania rachunku różniczkowego. przestała być grą dla amatorów - stała się pracą dla profesjonalistów ".
Abraham de Moivre (1667-1754), Johann Carl Friedrich Gauss (1777-1855), Pierre-Simon Laplace (1749-1827)
W 1733 r. Francuski matematyk Abraham de Moivre jako pierwszy opisał krzywą rozkładu normalnego lub prawo błędów w Approximatio ad summam tenninorum binomii (a + b)n in seriem expansi ("Approximation to the Sum of the Terms of a Binomial (a + b)n Expanded as a Series "). Przez całe życie de Moivre pozostawał biedny i zarabiał na boku, grając w szachy w kawiarniach. Normalna dystrybucja - zwana także dystrybucją Gaussa, na cześć Carla Friedricha Gaussa, który później badał krzywą - reprezentuje ważny nieprzewidywalny ciągły rozkład prawdopodobieństwa, który jest stosowany w polach CountIess, w których dokonywane są obserwacje. Obejmują one badania demografii populacji, statystyki zdrowia, pomiarów astronomicznych, dziedziczności, inteligencji, statystyki ubezpieczeń i wszelkich pola, w których występuje vanation w danych eksperymentalnych i obserwowanych cechach. W rzeczywistości, na początku XVIII wieku, matematycy zaczęli zdawać sobie sprawę, że ogromna liczba różnych pomiarów
wykazuje zwykle podobną formę rozpraszania lub rozkładu. Rozkład normalny jest definiowany przez dwa kluczowe parametry, średnia (lub średnia) i odchylenie standardowe, które określają ilościowo rozpiętość lub zmienność danych. rozkład rmal, gdy jest wykreślany, jest często nazywany krzywą dzwonową ze względu na jego symetryczny kształt dzwonka z wartościami bardziej skoncentrowanymi w środku niż w ogonach po bokach krzywej. De Moivre badał rozkład normalny podczas swoich badań aproksymacji do rozkładu dwumianowego. co powstaje na przykład podczas eksperymentów z rzucaniem monetą. PierreSimon Laplace zastosował rozkład w 1783 r. Do badania błędów pomiarowych. Gauss zastosował go w 1809 r. Do badania danych astronomicznych. Antropolog Sir Francis Galton napisał o normalnym rozkładzie: "Nie znam prawie niczego, co mogłoby zaimponować wyobraźni, jak cudowna forma kosmicznego porządku wyrażona w" prawie częstotliwości błędów: prawo byłoby personifikowane przez Greków i ubóstwiany, gdyby o tym wiedzieli. Panuje
w nim spokój i całkowite zniszczenie w najdzikszym zamieszaniu.
Leonhard Paul Euler (1707-1783), Lorenzo Mascheroni (1750-1800)
Stała Eulera-Mascheroniego, oznaczona literą grecką γ, ma wartość liczbową 0,5772157… Liczba ta łączy wykładnicze i logarytmy z teorią liczb i jest zdefiniowana przez granicę (1+1/2+1/3 +… + l/n - log n), gdy n zbliża się do nieskończoności. Zasięg γjest szeroki i szeroki, ponieważ odgrywa rolę w tak różnorodnych obszarach, jak nieskończone szeregi, iloczynach, prawdopodobieństwie i określone całkowe reprezentacje. Na przykład średnia liczba dzielników wszystkich liczb od 1 do n jest bardzo zbliżona do In n + 2γ - 1. Obliczanie &gamma nie cieszyło się takim samym zainteresowaniem publicznym jak obliczanie π, ale γ wciąż inspirowało wielu żarliwych wielbicieli. Chociaż obecnie znamy π do 1 241 100 000 000 miejsc po przecinku, w 2008 roku znanych było tylko około 10 000 000 000 miejsc γ. Wyliczanie γ jest znacznie trudniejsze niż π. Oto kilka pierwszych cyfr: 0,5772 1566490153286060651209008240243104215933593992…
Ta stała matematyczna ma długą i fascynującą historię, podobnie jak inne znane stałe, takie jak π i e. Szwajcarski matematyk Leonhard Euler omówił - w artykule. "De Progressionibus hannonicis observationes" ("Obserwacje postępów harmonicznych"), opublikowany w 1735 r., ale w tym czasie był w stanie obliczyć go z dokładnością do sześciu miejsc po przecinku. W 1790 roku włoski matematyk i ksiądz Lorenzo Mascheroni obliczyli dodatkowe cyfry. Dziś nie wiemy, czy liczbę można wyrazić jako ułamek (w taki sposób, że liczbę taką jak 0.1428571428571 ... można wyrazić jako In). Julian Havil, który poświęcił całą książkę γ, opowiada o historiach, w których angielski matematyk C. H. Hardy zaproponował, że zrezygnuje z katedry Savilian w Oxfordzie każdemu, kto udowodni, że -nie można wyrazić ułamkiem.
Leonhard Paul Euler (1707-1783)
Teoria grafów to dziedzina matematyki, która dotyczy sposobu łączenia obiektów i często upraszcza problemy, przedstawiając je jako kropki połączone liniami. Jednym z najstarszych problemów teorii grafów jest siedem mostów w Królewcu w Niemczech (obecnie część Rosji). Ludzie ze starego Królewca uwielbiali spacerować wzdłuż rzeki, mostów i wysp. Na początku XVIII wieku ludzie wciąż zastanawiali się, czy można odbyć podróż przez wszystkie siedem mostów bez konieczności przekraczania jednego mostu więcej niż jeden raz i powrotu do miejsca początkowego. Wreszcie w 1736 r. Szwajcarski matematyk Leonhard Euler udowodnił, że taka wycieczka była niemożliwa. Euler przedstawiał mosty za pomocą wykresu, na którym obszary lądowe są reprezentowane przez kropki, a mosty liniami. Pokazał, że można przejść przez taki wykres, przechodząc przez każdy segment tylko raz, jeśli wykres ma mniej niż trzy wierzchołki nieparzystej wartościowości. (Wartościowość wierzchołka to liczba linii, które zaczynają się lub zatrzymują na wierzchołku.) Mosty w Królewcu nie miały właściwej charakterystyki graficznej; dlatego nie jest możliwe przechodzenie przez wykres bez przechodzenia przez linię więcej niż jeden raz. Euler uogólnił swoje ustalenia na podróże po dowolnej sieci mostów. Problem mostu w Królewcu jest ważny w historii matematyki, ponieważ rozwiązanie Eulera odpowiada pierwszemu twierdzeniu w teorii grafów. Obecnie teorię grafów stosuje się w niezliczonych dziedzinach, od badania ścieżek chemicznych i przepływu ruchu samochodowego po sieci społecznościowe użytkowników Internetu. Teoria grafów może nawet wyjaśnić, jak rozprzestrzeniają się choroby przenoszone drogą płciową. Bardzo proste reprezentacje Eulera dotyczące połączeń mostów, bez względu na specyfikę długości mostów, były prekursorem topologii, pola matematycznego dotyczącego kształtów i ich wzajemnych relacji.
Daniel Bernoulli (1700-1782)
Daniel Bernoulli, urodzony w Holandii szwajcarski matematyk, fizyk i lekarz, napisał fascynujący artykuł na temat prawdopodobieństwa, który został ostatecznie opublikowany w 1738 r. W komentarzach Cesarskiej Akademii Nauk w Sankt Petersburgu. W artykule opisano paradoks znany obecnie jako Paradoks Sankt Petersburski, który można wyrazić w postaci rzutów monetą i pieniędzy, które gracz ma otrzymać, w zależności od wyniku tych rzutów. Filozofowie i matematycy długo dyskutowali o tym, jaka powinna być uczciwa cena za dołączenie do gry. Ile byłbyś gotowy zapłacić za dołączenie do tej działalności? Oto jeden ze sposobów przeglądania scenariusza z St.Petersburga. Odwróć grosz, aż wyląduje na reszce. Całkowita liczba rzutów, n, określa nagrodę, która wynosi 2n$. Tak więc, jeśli grosz po raz pierwszy wyląduje na ogonach, nagroda wynosi 21$ = 2$, a gra się kończy. Jeśli grosz pojawia się po raz pierwszy, zostaje ponownie obrócony. Jeśli pojawi się reszka za drugim razem, nagroda wynosi 22 $, = 4 $, a gra się kończy. I tak dalej. Szczegółowa dyskusja na temat paradoksu tej gry wykracza poza zakres tej książki, ale zgodnie z teorią gry "racjonalny hazardzista" wszedłby do gry wtedy i tylko wtedy, gdy cena wejścia była niższa niż oczekiwana wartość finansowa wypłata. W niektórych analizach . Gra w St. Petersburgu, każda skończona cena wejścia jest niższa niż oczekiwana wartość gry, a racjonalny gracz może chcieć w nią grać, bez względu na to, jak wysokie ustalimy skończoną cenę wejścia. I Peter Bernstein komentuje głębię paradoksu Bernoulliego: " Jego praca jest jednym z najgłębszych dokumentów, jakie kiedykolwiek napisano, nie tylko na temat ryzyka, ale na temat także ludzkie zachowanie. Nacisk Bernoulliego na złożone powiązania między pomiarem a jelitami dotyczy niemal każdego spektrum życia. "
Christian Goldbach (1690-1764), Leonhard Paul Euler (1707-1783)
Czasami najtrudniejsze problemy matematyczne należą do najłatwiejszych i najłatwiejszych do stwierdzenia. W 1742 r. pruski historyk i matematyk Christian Goldbach przypuszczał, że każdą liczbę całkowitą większą niż 5 można zapisać jako sumę trzech liczb pierwszych, takich jak 21 = 11 + 7 + 3. (Liczba pierwsza jest liczbą większą niż ja, na przykład jako 5 lub 13, które można podzielić tylko przez siebie lub 1.) Zgodnie z ponownym wyrażeniem szwajcarskiego matematyka Leonharda Eulera, równoważna hipoteza (zwana hipotezą "silnego" Goldbacha) stwierdza, że wszystkie dodatnie liczby całkowite większe niż 2 można wyrazić jako suma dwóch liczb pierwszych. Aby promować powieść "Wujek Petros" i "Konsekwencja Goldbacha", gigant wydawniczy Faber i Faber zaoferowali nagrodę w wysokości 1 000 000 USD każdemu, kto udowodnił hipotezę Goldbacha między 20 marca 2000 r. a 20 marca 2002 r., ale nagroda nie została odebrana, a przypuszczenie pozostaje otwarte. W 2008 r. Tomas Oliveira e Silva, badacz z University of Aveiro, Portugalia, przeprowadził rozproszone wyszukiwanie komputerowe, które zweryfikowało przypuszczenie do 12 ⋅ 1017 Oczywiście żadna moc obliczeniowa nie może potwierdzić przypuszczenia dla każdej liczby; matematycy mają zatem nadzieję na prawdziwy dowód słuszności intuicji Goldbacha. W 1966 r. Chiński matematyk Chen Jing-Run poczynił pewne postępy, gdy udowodnił, że każda wystarczająco duża liczba parzysta jest sumą jednej liczby pierwszej, plus liczba, która jest iloczynem co najwyżej dwóch liczb pierwszych. Na przykład 18 jest równe 3 + (3 X 5). W 1995 r. Francuski matematyk Olivier Ramare wykazał, że każda liczba parzysta większa lub równa 4 jest sumą co najwyżej sześciu liczb pierwszych
Maria Gaetana Agnesi (1718-1799)
Włoska matematyk Maria Agnesi jest autorką Instituzioni analitiche (Analytical Institutions), pierwszego obszernego podręcznika, który obejmował zarówno rachunek różniczkowy, jak i całkowy, oraz pierwszego ocalałego dzieła matematycznego napisanego przez kobietę. Holenderski matematyk Dirk Jan Struik nazwał Agnesi "pierwszą ważną matematyczką od czasów Hypatii (AD piąty wiek)". Agnesi była cudownym dzieckiem, mówiła w co najmniej siedmiu językach w wieku 13 lat. Przez większość swojego życia unikała interakcji społecznych i całkowicie poświęciła się nauce matematyki i religii. Clifford Truesdell pisze: "Poprosiła ojca, by został zakonnicą. Przerażony, że jego najdroższe dziecko może go opuścić, błagał ją, by zmieniła zdanie". Zgodziła się kontynuować życie z ojcem, o ile będzie mogła żyć we względnym odosobnieniu. Publikacja Instituzioni analitiche wywołała sensację w świecie akademickim. Komitet Academie des Sciences w Paryżu napisał: "Zmniejszenie umiejętności wymagało wielu umiejętności i mądrości … do prawie jednolitych metod odkrycia te rozrzucone były wśród dzieł współczesnych matematyków i często przedstawiane metodami bardzo różniącymi się od siebie. Porządek, jasność i precyzja panuje we wszystkich częściach tej pracy … Uważamy ją za najbardziej kompletny i najlepiej wykonany traktat. " Książka zawiera również omówienie krzywej sześciennej znanej obecnie jako Wiedźma Agnesi i wyrażonej jako y= 8a3 / (x2 + 4a2).
Prezydent Akademii Bolońskiej zaprosił Agnesi do przyjęcia Katedry Mathematyki na Uniwersytecie Bolońskim. Według niektórych relacji nigdy tak naprawdę nie pojechała do Bolonii, ponieważ w tym czasie całkowicie poświęciła się religii i działalności charytatywnej. Niemniej jednak uczyniło ją drugą kobietą, która została profesorem na uniwersytecie; pierwszym była Laura Bassi (1711-1778). Agnesi wydała wszystkie pieniądze na pomoc biednym i zmarła w całości w ubogim domu.
Leonhard Paul Euler (1707-1783), Rene Descartes (1596--1650), Paul Erdös (1913-1996)
Wzór Eulera dla wielościanów jest uważana za jedną z najpiękniejszych formuł w całej matematyce i jedną z pierwszych świetnych formuł topologii - badania kształtów i ich wzajemnych powiązań. Badanie przeprowadzone wśród czytelników Mathematical Intelligencer umieściło formułę jako drugą najpiękniejszą formułę w historii, drugą po Euler eiπ + 1 = 0, omówioną w opisie Liczby Eulera, e (1727).
W 1751 roku szwajcarski matematyk i fizyk Leonhard Euler odkrył, że każdy wypukły wielościan (obiekt o powierzchniach kapelusza i prostych krawędziach), o wierzchołkach V, krawędziach E i ścianach F, spełnia równanie V - E + F = 2. Wielościan jest wypukły, jeśli nie ma wgłębień ani otworów, lub bardziej formalnie, jeśli każdy segment linii łączący punkty wewnętrzne jest całkowicie zawarty we wnętrzu figury. Na przykład powierzchnia sześcianu ma sześć ścian, dwanaście krawędzi i osiem wierzchołków. Wstawiając te wartości do wzoru Eulera, otrzymujemy 6 - 12 + 8 = 12. Dla dwunastościanu z jego 12 ścianami mamy 20 - 30 + 12 = 2. Co ciekawe, około 1639 r. Rene Descartes odkrył pokrewną wielościenną formułę, która może być przekonwertowany na formułę Eulera w kilku matematycznych krokach. Formuła wielościanu została później uogólniona do badania sieci i grafów, aby pomóc matematykom zrozumieć szeroki zakres kształtów z dziurami i w większych wymiarach. Ta formuła ułatwia również wiele praktycznych zastosowań, takich jak pomaganie specjalistom komputerowym w znajdowaniu sposobów ułożenia ścieżek w obwodach elektrycznych, a kosmolodzy zastanawiają się nad modelami kształtu naszego wszechświata. Euler jest drugim po Węgrzech Paulem Erdosem jako najbardziej płodnym matematykiem w historii pod względem liczby publikacji. Niestety Euler oślepł pod koniec życia. Jednak pisarz naukowy Bribsh David Darling zauważa: "wielkość jego twórczości wydawała się odwrotnie proporcjonalna do jakości jego wzroku, ponieważ jego tempo publikacji wzrosło po tym, jak prawie całkowicie stracił wzrok w 1766 roku"
Wzór Eulera dla wielościanów jest uważana za jedną z najpiękniejszych formuł w całej matematyce i jedną z pierwszych świetnych formuł topologii - badania kształtów i ich wzajemnych powiązań. Badanie przeprowadzone wśród czytelników Mathematical Intelligencer umieściło formułę jako drugą najpiękniejszą formułę w historii, drugą po Euler eiπ + 1 = 0, omówioną w opisie Liczby Eulera, e (1727). W 1751 roku szwajcarski matematyk i fizyk Leonhard Euler odkrył, że każdy wypukły wielościan (obiekt o powierzchniach kapelusza i prostych krawędziach), o wierzchołkach V, krawędziach E i ścianach F, spełnia równanie V - E + F = 2. Wielościan jest wypukły, jeśli nie ma wgłębień ani otworów, lub bardziej formalnie, jeśli każdy segment linii łączący punkty wewnętrzne jest całkowicie zawarty we wnętrzu figury. Na przykład powierzchnia sześcianu ma sześć ścian, dwanaście krawędzi i osiem wierzchołków. Wstawiając te wartości do wzoru Eulera, otrzymujemy 6 - 12 + 8 = 12. Dla dwunastościanu z jego 12 ścianami mamy 20 - 30 + 12 = 2. Co ciekawe, około 1639 r. Rene Descartes odkrył pokrewną wielościenną formułę, która może być przekonwertowany na formułę Eulera w kilku matematycznych krokach. Formuła wielościanu została później uogólniona do badania sieci i grafów, aby pomóc matematykom zrozumieć szeroki zakres kształtów z dziurami i w większych wymiarach. Ta formuła ułatwia również wiele praktycznych zastosowań, takich jak pomaganie specjalistom komputerowym w znajdowaniu sposobów ułożenia ścieżek w obwodach elektrycznych, a kosmolodzy zastanawiają się nad modelami kształtu naszego wszechświata. Euler jest drugim po Węgrzech Paulem Erdosem jako najbardziej płodnym matematykiem w historii pod względem liczby publikacji. Niestety Euler oślepł pod koniec życia. Jednak pisarz naukowy Bribsh David Darling zauważa: "wielkość jego twórczości wydawała się odwrotnie proporcjonalna do jakości jego wzroku, ponieważ jego tempo publikacji wzrosło po tym, jak prawie całkowicie stracił wzrok w 1766 roku"
Leonhard Paul Euler (1707-1783)
W 1751 r. Szwajcarski matematyk Leonhard Paul Euler postawił następujący problem pruskiemu matematykowi Christianowi Goldbachowi (1690-1764): Na ile sposobów En płaskiego wypukłego wielokąta n boków można podzielić na trójkąty po przekątnych? Lub, mówiąc bardziej nieformalnie: na ile sposobów możesz podzielić wielokątne ciasto na trójkąty, zaczynając od prostych cięć nożem w dół od jednego rogu, a kończąc na innym? Twoje cięcia nie mogą się przecinać. Wzór znaleziony przez Eulera była następująca:
En = 2 ⋅ 6 ⋅ 10 …… (4n - 10) / (n - 1)!
Wielokąt jest wypukły, jeśli dla każdej pary punktów należących do kształtu kształt zawiera cały segment linii prostej łączący dwa punkty. Autor i matematyk Heinrich Dorrie pisze: "Ten problem jest szczególnie interesujący, ponieważ wiąże się z wieloma trudnościami pomimo jego nieszkodliwego wyglądu, a wiele czytelnik odkryje. …" Sam Euler powiedział: Zastosowany przeze mnie proces indukcji był dość pracochłonny ... Na przykład dla kwadratu mamy E4 = 2, co odpowiada dwóm przekątnym. Dla pięciokąta mamy E5 = 5. W rzeczywistości wcześniejsi eksperymentatorzy byli skłonni do korzystania z reprezentacji graficznych, aby wyczuć rozwiązanie, ale to podejście wizualne wkrótce staje się trudne do rozwiązania wraz ze wzrostem liczby boków wielokąta. Zanim dojdziemy do 9-stronnego wielokąta, mamy 429 sposobów na podzielenie wielokąta na trójkąty przez przekątne. Problem podziału wieloboków przyciągnął wiele uwagi. W 1758 r. Matematyk CarpathoGerman Johann Andreas Segner (1704-1777) opracował wzór rekurencyjny do określania wartości: En = E2En-1 + E3En-2 + … + En-1 - E2 . Formuła rekurencyjna to taka, w której każdy termin sekwencji jest zdefiniowany jako funkcja poprzednich terminów. Co ciekawe, wartości En są ściśle związane z inną klasą liczb zwaną liczbami Catallana (En = Cn-1). Liczby Catallana powstają w kombinatoryce, w dziedzinie matematyki związanej z problemami wyboru, układu i działania w systemie skończonym lub dyskretnym.
Abraham de Moivre (1667-1754), Leonhard Paul Euler (1707-1783), Adrien-Marie Legendre (1752-1833)
Aby stworzyć Wycieczki Rycerskie, szachy muszą skakać dokładnie raz na każde pole na szachownicy 8 x 8 podczas pełnej trasy. Różne rodzaje wycieczek rycerskich fascynują matematyków od stuleci. Najwcześniejsze zarejestrowane rozwiązanie dostarczył Abraham de Moivre, francuski matematyk lepiej znany z krzywej rozkładu normalnegoi jego twierdzeń o liczbach zespolonych. W swoim rozwiązaniu rycerz kończy zwiedzanie na kwadracie, który jest daleko od jego pozycji początkowej. Francuski matematyk AdrienMarie Legendre "poprawił" to i znalazł rozwiązanie, w którym pierwszy i ostatni kwadrat są jednym ruchem od siebie, tak więc trasa zamyka się w pojedynczej pętli 64 ruchów rycerza. Mówi się, że taka wycieczka jest reentrantem. Szwajcarski matematyk Leonhard Euler znalazł trasę powrotną, która odwiedza dwie połówki tablicy w całości. Euler jako pierwszy napisał artykuł matematyczny analizujący Wycieczki rycerskie.. Przedstawił artykuł Akademii Nauk w Berlinie w 1759 r., ale ten wpływowy artykuł nie został opublikowany aż do 1776 r. Co ciekawe, w 1759 roku Akademia zaproponowała nagrodę w wysokości 4000 franków za najlepsze wspomnienie z Wycieczek rycerskich, ale nagroda nigdy nie została przyznana, być może dlatego, że Euler był dyrektorem matematyki w berlińskiej Akademii i nie kwalifikował się do nagrody. Henry E. Dudeney przedstawił trasę po sześcianie w swojej książce Amusement in Mathematics, i sądzę, że oparł rozwiązanie (w którym każda twarz jest kolejno zwiedzana) na wcześniejszej pracy francuskiego matematyka Alexandre-Theophile Vandermonde (1735-1796). Odtąd właściwości Wycieczek rycerskich zostały dokładnie zbadane na szachownicach na powierzchniach cylindra, paska Mobius Strip, torusa i butelki Kleina, a nawet w większych wymiarach.
Thomas Bayes (ok. 1702-1761)
Twierdzenie Bayesa, sformułowane przez brytyjskiego matematyka i prezbiteriańskiego księdza Thomasa Bayesa, odgrywa fundamentalną rolę w nauce i można je sformułować prostym wzorem matematycznym stosowanym do obliczania prawdopodobieństw warunkowych. Prawdopodobieństwo warunkowe odnosi się do prawdopodobieństwo pewnego zdarzenia A, biorąc pod uwagę wystąpienie innego zdarzenia B, zapisanego jako P(A|B). Twierdzenie Bayesa stwierdza: P(A|B)=[P(B|A) x P(A)]/P(B). Tutaj P(A) nazywa się wcześniejszym prawdopodobieństwem A, ponieważ jest to prawdopodobieństwo zdarzenia A bez uwzględnienia niczego, co wiemy o B. P(B|A) to warunkowe prawdopodobieństwo B, biorąc pod uwagę A. P(B) to wcześniejsze prawdopodobieństwo B Wyobraź sobie, że mamy dwa pudełka. Pudełko 1I ma 10 piłek golfowych i 30 piłek bilardowych. Pudełko 2 zawiera po 20 sztuk. Wybierasz losowo pudełko i wyciągasz piłkę. Zakładamy, że równie prawdopodobne jest wybranie piłek. Twoja piłka okazuje się być piłką bilardową. Jak prawdopodobne jest, że wybrałeś Pudełko 1? Innymi słowy, jakie jest prawdopodobieństwo, że wybrałeś Pudełko 1, biorąc pod uwagę, że masz w ręce piłkę bilardową? Zdarzenie A odpowiada Twojemu polu wyboru. Zdarzenie B to wybranie piłki bilardowej. Chcemy obliczyć P(A|B). P(A) wynosi 0,5 lub 50 procent. P(B) to prawdopodobieństwo wybrania piłki bilardowej niezależnie od jakichkolwiek informacji na polach. Jest on obliczany jako suma prawdopodobieństwa otrzymania piłki bilardowej ze skrzynki pomnożona przez prawdopodobieństwo wyboru pudełka. Prawdopodobieństwo wybrania piłki bilardowej z pola I wynosi 0,75. Prawdopodobieństwo wybrania jednego z pola 2 wynosi 0,5. Prawdopodobieństwo uzyskania ogólnej piłki bilardowej wynosi 0,75 x 0,5 + 0,5 x 0,5 = 0,625. P(B|A) lub prawdopodobieństwo otrzymania piłki bilardowej, biorąc pod uwagę, że wybrałeś pole I, wynosi 0,75. Możemy użyć wzoru Bayesa, aby ustalić, że prawdopodobieństwo wybrania przez Ciebie Pudełko 1, czyli P(A|B) = 0,6.
Benjamin Franklin (1706-1790)
Benjamin Franklin był naukowcem, wynalazcą, mężem stanu, drukarzem, filozofem , muzykiem i ekonomistą. W 1769 roku, w liście do kolegi, opisuje Magiczny kwadrat, który stworzył wcześniej w swoim życiu. Jego magiczny kwadrat 8 x 8 jest wypełniony cudownymi symetriami, o których pewnie Ben Franklin prawdopodobnie nie był świadomy. Każdy rząd i kolumna kwadratu ma sumę 260. Połowa każdego rzędu lub kolumny sumuje się do połowy 260. Ponadto każdy z wygiętych wierszy ma sumę 260. Zobacz dwa podświetlone szare kwadraty dla dwóch przykładów wygiętych rzędów. Zobacz kwadraty z grubymi czarnymi ramkami na przykład złamanego wygiętego rzędu (14 + 61 + 64 + 15 + 18 + 33 + 36 + 19), który również wynosi 260. Można znaleźć wiele innych symetrii - na przykład cztery kolejne liczby i cztery środkowe liczby sumują się do 260. Suma liczb w dowolnym kwadracie 2 x 2 wynosi 130, a suma dowolnych czterech liczb ułożonych w równej odległości od środka kwadratu równa się również 130. Po przeliczeniu na liczby binarne, znaleziono jeszcze więcej zaskakujących symetrii. Niestety, pomimo wszystkich cudownych symetrii, główne przekątne nie sumują się do 260, więc nie można tego ściśle zakwalifikować jako magiczny kwadrat zgodnie ze wspólną definicją, która obejmuje sumy przekątne. Nie wiemy, jaką metodą Franklin zbudował swoje kwadraty. Wiele osób próbowało złamać tajemnicę, ale do lat 90. nie można było znaleźć szybkiego przepisu, chociaż Franklin twierdził, że może wygenerować kwadraty tak szybko, jak potrafił napisać: W 1991 roku autor Lalbhai Patel wynalazł metodę konstruowania kwadratów Franklina. Chociaż metoda wydaje się dość długa, Patel wyszkolił się, aby szybko przeprowadzić procedurę. Na magicznym kwadracie Franklina znaleziono tak wiele wspaniałych wzorów, że ten kwadrat stał się metaforą dla obiektów matematycznych zawierających symetrie i inne właściwości, które wciąż odkrywane są długo po śmierci wynalazcy.
Leonhard Paul Euler (1707-1783), Jean Meusnier (1754-1793), Heinrich Ferdinand Scherk (1798-1885)
Wyobraź sobie, że wyjmujesz pierścień z drutu z wody z mydłem. Ponieważ pierścień zawiera błonę mydlaną w kształcie dysku, która ma mniejszą powierzchnię niż inne kształty, które hipotetycznie mogły powstać, matematycy nazywają tą powierzchnię minimalną powierzchnią. Bardziej formalnie, skończona minimalna powierzchnia jest często charakteryzowana jako posiadająca najmniejszy możliwy obszar ograniczony daną zamkniętą krzywą lub krzywymi. Średnia krzywizna powierzchni wynosi zero. Poszukiwanie przez matematyka minimalnych powierzchni i dowodów ich minimalności trwało ponad dwa stulecia. Minimalne powierzchnie z krzywymi ograniczającymi, które skręcają się do trzeciego wymiaru, mogą być zarówno piękne, jak i skomplikowane. W 1744 roku szwajcarski matematyk Leonhard Euler odkrył katenoid, pierwszy przykład minimalnej powierzchni poza zwykłymi przykładami, takimi jak obszary okrągłe. W 1776 r. Francuski geometria Jean Meusnier odkrył minimalną powierzchnię helikoidy. (Meusnier był także generałem wojskowym i projektantem pierwszego śmigłowego balonu w kształcie elipsy do noszenia ludzi). Kolejnej minimalnej powierzchni nie znaleziono aż do 1873 r. Niemiecki matematyk Heinrich Scherk. W tym samym roku belgijski fizyk Joseph Plateau przeprowadził eksperymenty, które doprowadziły go do przypuszczenia, że bańki mydlane zawsze tworzą minimalne powierzchnie. "Problem Plateau" dotyczy matematyki wymaganej do udowodnienia, że to prawda. (Plateau stał się ślepy w wyniku wpatrywania się w słońce przez 25 sekund w eksperymencie dotyczącym fizjologii wzroku). Nowsze przykłady obejmują minimalną powierzchnię Costa, którą po raz pierwszy opisał matematycznie w 1982 r. Brazylijski matematyk Celso Costa. Komputery i grafika komputerowa odgrywają obecnie istotną rolę w pomaganiu matematykom w tworzeniu i wizualizacji minimalnych powierzchni, z których niektóre mogą być dość skomplikowane. Powierzchnie Minimalne mogą pewnego dnia mieć wiele zastosowań w inżynierii materiałowej i nanotechnologii. Na przykład niektóre polimery po zmieszaniu tworzą interfejsy o minimalnej powierzchni. Znajomość kształtów interfejsów może pomóc naukowcom przewidzieć właściwości chemiczne takich mieszanin.
Georges-Louis Leclerc, Comte de Buffon (1707-1788)
Nazwane na cześć słynnej z wielu kasyn dzielnicy Monako, metody Monte Carlo odgrywają kluczową rolę w matematyce i nauce oraz wykorzystują losowość w celu rozwiązania problemów, od statystyki reakcji łańcucha nuklearnego po regulację przepływów ruchu. Jedno z najwcześniejszych i najbardziej znanych zastosowań tej metody miało miejsce w XVIII wieku, kiedy francuski przyrodnik i matematyk Comte de Buffon wykazał, że przez kilkakrotne upuszczanie igły na kartkę papieru i liczenie, ile razy igła dotknęła linii, mógł uzyskać oszacowanie wartości stałej matematycznej pi (π = 3,1415…). W najprostszym przypadku wyobraź sobie, że upuszczasz wykałaczkę na podłogę z twardego drewna, a odstępy między liniami podłogi są równe długości wykałaczki. Aby oszacować liczbę pi z kropli wykałaczki, po prostu rozważ liczbę kropli i pomnóż ją przez 2, a następnie podziel przez liczbę przypadków, gdy wykałaczka dotknęła linii. Buffon był człowiekiem o wielu talentach. Jego 36-tomowa Histoire naturelle, generale et Partuliere (Historia naturalna; Ogólna i szczególna) zawiera wszystko, co wiadomo o świecie przyrody i wpłynęło na Charlesa Darwina i teorię ewolucji. Obecnie potężne komputery mogą generować ogromne ilości liczb pseudolosowych na sekundę i pozwalają naukowcom w pełni wykorzystać metody Monte Carlo w celu zrozumienia problemów w ekonomii, fizyce, chemii, prognozowaniu struktury białek, tworzeniu galaktyki, sztucznej inteligencji, terapii przeciwnowotworowej, zapasach prognozowanie, eksploracja szybów naftowych, projektowanie aerodynamicznych kształtów oraz problemy w czystej matematyce, dla których nie są dostępne żadne inne metody. W czasach współczesnych matematycy i fizycy, tacy jak Stanisław Ulam, John von Neumann, Nicholas Metropolis i Enrico Fermi, zwrócili uwagę świata na świat. Fermi zastosował to podejście do badania propemów neutronu. Metody Monte Carlo mają kluczowe znaczenie dla symulacji wymaganych dla Manhattan Project, amerykańskiego programu rozwoju bomby atomowej podczas II wojny światowej.
Leonhard Paul Euler (1707-1783), Gaston Tarry (1843-1913)
Rozważy sześć pułków wojskowych, z których każdy składa się z sześciu oficerów różnych stopni. W 1779 r. Leonhard Euler zapytał, czy możliwe jest rozmieszczenie tych 36 oficerów w układzie kwadratowym 6 x 6, tak aby jeden oficer z każdego z sześciu pułków pojawił się w każdym rzędzie, a jeden z każdego z sześciu stopni pojawił się w każdej kolumnie. W języku matematyki problem ten jest równoznaczny ze znalezieniem dwóch wzajemnie prostopadłych kwadratów łacińskich rzędu sześciu. Euler poprawnie przypuszczał, że nie ma rozwiązania, a francuski matematyk Gaston Tarry udowodnił to w 1901 r. Przez wieki problem doprowadził do znacznych prac w kombinatoryce, w dziedzinie matematyki związanej z wyborem i rozmieszczeniem przedmiotów. Kwadraty łacińskie odgrywają również rolę w kodach korygujących błędy i komunikacji. Kwadrat łaciński składa się z n zestawów liczb, od 1 do n, ułożonych w taki sposób, że żaden wiersz lub kolumna nie zawiera tych samych dwóch liczb. Liczby kwadratów łacińskich rozpoczynających się od rzędu n = 1 wynoszą 1,2,12,576,161,280,812,851,200,61,479,419,904,000, 108 776 032,459,082,956,800 i tak dalej.
Mówi się, że para kwadratów łacińskich jest ortogonalna, jeśli pary n2 utworzone przez zestawienie dwóch tablic są różne. (Łączenie w sobie odnosi się do łączenia dwóch liczb w celu utworzenia uporządkowanej pary). Euler przypuszczał, że jeśli n = 4k + 2, gdzie k jest dodatnią liczbą całkowitą, to nie istnieje para ortogonalnych n x n kwadratów łacińskich. Ta hipoteza nie została rozstrzygnięta przez ponad sto lat, aż do 1959 r., Kiedy to matematycy Bose, Shikhande i Parker zbudowali parę prostokątnych kwadratów łacińskich 22 x 22. Dziś wiemy, że dla każdej dodatniej liczby całkowitej n istnieje para ortogonalnych n x n kwadratów łacińskich, z wyjątkiem n = 2 i n = 6.
Fujita Kagen (1765-1821)
Tradycja znana jako Sangaku, czyli "japońska geometria świątynna", powstała w japońskim okresie izolacji od Zachodu, mniej więcej w latach 1639-1854. Matematycy, fani, samurajowie, kobiety i dzieci rozwiązali trudne problemy z geometrią i zapisali rozwiązania na tabliczkach. Te kolorowe tabliczki zostały następnie zawieszone pod dachy świątyń. Przetrwało ponad 800 tabliczek, a wiele z nich ma problemy z kołami stycznymi. W 1789 r. Japoński matematyk Fujita Kagen opublikował Shimpeki Sampo (Problemy matematyczne zawieszone przed świątynią), pierwszy zbiór problemów Sangaku. Najstarsza zachowana tabliczka pochodzi z 1683 roku, chociaż inne dokumenty historyczne odnoszą się do przykładów już w 1668 roku. Większość Sangaku dziwnie różni się od typowych problemów z geometrią występujących w podręcznikach, ponieważ miłośnicy Sangaku zwykle mieli obsesję na punkcie kół i elips. Niektóre problemy Sangaku są tak trudne, że fizyk Tony Rothman i pedagog Hidetoshi Fukagawa piszą: "Geometria nowoczesna niezmiennie rozwiązuje je za pomocą zaawansowanych metod, w tym rachunku różniczkowego i afinicznego." Jednak unikając rachunku różniczkowego. Problemy Sangaku były w zasadzie wystarczająco proste, aby dzieci mogły je rozwiązać przy pewnym wysiłku. Chad Boutin pisze: "Być może nie jest zaskakujące, że Sudoku - liczba zagadek, nad którymi wszyscy wydają się pracować w tych dniach - po raz pierwszy stała się popularna w Japonii, zanim rozprzestrzeniła się po oceanie. , kiedy zagorzali entuzjaści posunęli się, aby wrzucić najpiękniejsze rozwiązania geometryczne do precyzyjnie ilustrowanych drewnianych tabliczek, zwanych Sangaku ... "
Johann Carl Friedrich Gauss (1777-1855)
Wchodzisz do jaskini z cudownymi stalaktytami wystającymi z sufitu. Można oczekiwać, że istnieje korelacja między długością stalaktytu a jego wiekiem, chociaż związek między tymi dwiema zmiennymi może nie być dokładny. Nieprzewidywalne wahania temperatury i wilgotności prawdopodobnie wpływają na wzrost. Jednak przy założeniu, że istnieją chemiczne lub fizyczne metody szacowania wieku stalaktytu, z pewnością istnieje pewien trend między wiekiem a długością, który pozwala nam dokonywać przybliżonych prognoz. Metoda najmniejszych kwadratów odegrała kluczową rolę w nauce w wyjaśnianiu i wizualizowaniu takich trendów, a dziś metoda jest dostępna w większości statystycznych pakietów komputerowych, które rysują linie lub wygładzają krzywe za pomocą hałaśliwych danych eksperymentalnych. Najmniejsze kwadraty to matematyczna procedura znajdowania krzywej "najlepiej dopasowanej" dla danego zestawu punktów danych poprzez minimalizację sumy kwadratów przesunięć punktów z krzywej. W 1795 roku niemiecki matematyk i
naukowiec Carl Friedrich Gauss, w wieku 18 lat, zaczął opracowywać analizę metodą najmniejszych kwadratów. Zademonstrował wartość swojego podejścia w 1801 roku, kiedy przewidział przyszłe położenie asteroidy Ceres. Jako tło włoski astronom Giuseppe Piazzi (1746-1826) odkrył Ceres w 1800 r., Ale później asteroida zniknęła za słońcem i nie mogła zostać przeniesiona. Austriacki astronom Franz Xaver von Zach (1754-1832) zauważył, że "bez inteligentnej pracy i obliczeń doktora Gaussa nie moglibyśmy ponownie znaleźć Ceres". Co ciekawe, Gauss trzymał swoje metody w tajemnicy, aby utrzymać przewagę nad współczesnymi i poprawić swoją reputację. Później w swoim życiu czasami publikował wyniki naukowe jako szyfr, aby zawsze mógł udowodnić, że dokonał różnych odkryć, zanim inni to zrobili. Gauss ostatecznie opublikował swoją tajną metodę najmniejszych kwadratów w 1809 r. w swojej Teorii ruchu ciał niebieskich
Johann Carl Friedrich Ganss (1777-1855)
W 1796 roku, gdy Gauss był jeszcze nastolatkiem, odkrył sposób na zbudowanie regularnego 17-bocznego wielokąta, znanego również jako heptadekagon, przy użyciu prostej linii i cyrkla. Opublikował wynik w swojej monumentalnej pracy z 1801 r., Disquisitiones Arithmeticae (Disquisitiones Arithmetic). Konstrukcja Gaussa była bardzo znacząca, ponieważ od czasu Euklidesa podejmowano jedynie nieudane próby. Przez ponad 1000 lat matematycy umieli konstruować za pomocą cyrkla i prostej, regularne n-gony, w których n było wielokrotnością 3, 5, i potęgami 2. Gauss był w stanie dodać więcej wielokątów do tej listy, a mianowicie tych o największej liczbie boków postaci 22n +1, gdzie n jest liczbą całkowitą. Możemy utworzyć listę kilku pierwszych takich liczb: F0 = 3, F1 = 5, F2=17, F3 = 257 i F4 = 65 537. (Liczby w tej postaci są znane również jako liczby Fermata i niekoniecznie są pierwsze.) W 1832 roku zbudowano 257-gon. Kiedy był starszy, Gauss nadal uważał swoje 17-gonowe odkrycie za jedno ze swoich największych osiągnięć. 17-gon zostanie umieszczony na jego nagrobku. Według legendy kamieniarz odmówił, stwierdzając, że trudna konstrukcja zasadniczo sprawiłaby, że 17-gon wyglądałby jak koło. Rok 1796 był pomyślny dla Gaussa, kiedy jego pomysły tryskały jak fontanna z węża pożarowego. Oprócz rozwiązania konstrukcji heptadekagonu (30 marca) Gauss wynalazł arytmetykę modułową i przedstawił swoją kwadratową zasadę wzajemności (8 kwietnia) i twierdzenie o liczbie pierwszej (31 maja). Udowodnił, że każda dodatnia liczba całkowita jest reprezentowana jako suma co najwyżej trzech liczb trójkątnych (10 lipca). Odkrył także rozwiązania wielomianów o współczynnikach w polach skończonych (1 października). Jeśli chodzi o heptadekagon, Gauss powiedział, że był "zdumiony", że tak niewiele odkryto w odniesieniu do budowy wielokąta od czasów Euklidesa.
Johann Carl Friedrich Gauss (1777-1855)
Fundamentalne twierdzenie algebry (FTA) jest wyrażone w kilku formach, z których jedna jest taka, że każdy wielomian stopnia n ≥ 1 , z rzeczywistymi lub złożonymi współczynnikami, ma rzeczywiste lub złożone pierwiastki. Innymi słowy, wielomian P(x) stopnia n ma n wartości xi (niektóre z nich prawdopodobnie są powtarzane), dla których P(xi) = 0. Jako tło wielomianowe równania stopnia n mają postać P(x) = anxn + a an-1xn-1 + ... + a1x + a0 = 0 gdzie an ≠ 0. Jako przykład rozważmy kwadratowy wielomian f(x) = x2 - 4. Po wykreśleniu krzywa jest parabolą, a jej minimum wynosi x = - 4. Wielomian ma dwa różne rzeczywiste pierwiastki (x = 2 i x = - 2 ), które są graficznie postrzegane jako punkty, w których parabola przecina oś x. Twierdzenie to jest godne uwagi, częściowo ze względu na samą liczbę prób udowodnienia go poprzez historię. Niemiecki matematyk Carl Friedrich Gauss jest zwykle przypisywany pierwszemu dowodowi ITA, odkrytemu w 1797 r. W swojej pracy doktorskiej, opublikowanej w 1799 r., Przedstawił swój pierwszy dowód, który koncentrował się na wielomianach o rzeczywistych współczynnikach, a także na jego sprzeciwach wobec inne poprzednie próby dowodów. Zgodnie z dzisiejszymi standardami dowód Gaussa nie był rygorystycznie kompletny, ponieważ polegał na ciągłości niektórych krzywych, ale była to znacząca poprawa w stosunku do wszystkich poprzednich prób dowodu. Gauss uznał ITA za bardzo ważne, o czym świadczy jego wielokrotny powrót do problemu. Jego czwarty dowód znajduje się w ostatniej pracy, jaką kiedykolwiek napisał, która ukazała się w 1849 r., Dokładnie 50 lat po rozprawie. Należy zauważyć, że Jean-Robert Argand (1768-1822) opublikował rygorystyczny dowód na podstawowe twierdzenie algebry w 1806 r. Dla wielomianów o złożonych współczynnikach. ITA powstaje w wielu obszarach matematyki, a różne dowody obejmują pola, od abstrakcyjnej algebry i złożonej analizy do topologii.
Johann Carl Friedrich Gauss (1777-1855)
Stephen Hawking pisze: "Kiedy Gauss rozpoczął pracę nad swą epokową Disquisrtlones Arithmeticae (Arithmetic Disquisitions), teoria liczb była jedynie zbiorem izolowanych wyników ... W Disquisitiones wprowadził pojęcie zgodności i czyniąc to zunifikowaną teorią liczb." Gauss opublikował to monumentalne dzieło w wieku 24 lat. Disquisitiones obejmuje arytmetykę modułową, która opiera się na relacjach zgodności. Dwie liczby całkowite p i q to "przystające modulo liczby całkowite s" wtedy i tylko wtedy, gdy (p - q) jest równomiernie podzielne przez s. Taka zgodność jest zapisywana jako p ≡ q (mod s). Za pomocą tej zwartej notacji Gauss ponownie sformułował i udowodnił słynne twierdzenie o kwadratowej wzajemności, które kilka lat wcześniej zostało niekompletnie udowodnione przez francuskiego matematyka AdrienMarie Legendre (1752-1833). Rozważmy dwie różne nieparzyste liczby pierwsze, p i q. Rozważmy stwierdzenia: (1) p jest kwadrat mod q, a (2) q jest kwadratem mod p. Zgodnie z twierdzeniem: jeśli oba p i q są przystające do 3 (mod 4), to dokładnie jeden z (1) i (2) jest prawdziwy; w przeciwnym razie oba (1) i (2) są prawdziwe lub żaden z nich nie jest prawdziwy. (Kwadrat jest liczbą całkowitą, którą można zapisać jako kwadrat jakiejś innej liczby całkowitej, takiej jak 25, która wynosi 52) Zatem to twierdzenie łączy rozwiązywalność dwóch powiązanych równań kwadratowych w arytmetyce modułowej. Gauss poświęcił większą część swojej książki na dowód tego twierdzenia. Uważał to ukochane twierdzenie o kwadratowej wzajemności za "złote twierdzenie" lub "klejnot arytmetyki", które tak zafascynowały Gaussa, że w ciągu swojego życia przedstawił osiem odrębnych dowodów. Matematyk Leopold Kronecker powiedział: "To naprawdę zdumiewające, że samotny mężczyzna w tak młodym wieku był w stanie [przedstawić tak głębokie i dobrze zorganizowane podejście do zupełnie nowej dyscypliny". W Disquisitiones, podejście Gaussa do dostarczania twierdzeń, a następnie dowodów, następstw i przykładów zostało wykorzystane przez kolejnych autorów. Odkrycia były zarodkiem, z którego rozkwitało dzieło wielu wiodących dziewiętnastowiecznych teoretyków liczb
Joseph Huddart (1741-1816)
Dzisiejszym wspólnym kątomierzem jest instrument służący do konstruowania i mierzenia kątów na płaszczyźnie oraz do rysowania linii pod różnymi kątami. Kątomierz ten przypomina półkolisty dysk oznaczony stopniami, od 0o do 180o. W XVII wieku kątomierze zaczęły być używane jako samodzielne przyrządy, a nie jako części innych urządzeń, gdy żeglarze używali ich na mapach oceanicznych. W 1801 r. Joseph Huddart, angielski kapitan marynarki wojennej. wynalazł trójramienny kątomierz do kreślenia pozycji łodzi na mapach nawigacyjnych. Ten rodzaj kątomierza wykorzystuje dwa zewnętrzne ramiona, które mogą obracać się względem nieruchomego ramienia środkowego. Dwa obrotowe ramiona mogą być zaciśnięte, dzięki czemu można je ustawić pod ustalonymi kątami. W 1773 roku Huddart pracował dla Kompanii Wschodnioindyjskiej, żeglując na Wyspie St. Helena na Oceanie Południowoatlantyckim i Bencooleen na Sumatrze. Podczas swojej podróży dokonał szczegółowych badań zachodniego wybrzeża Sumatry. Jego mapa St
George′s Channel z 1778 roku, połączenie Morza Irlandzkiego z północą i Oceanem Atlantyckim z południowego zachodu było arcydziełem jasności i dokładności. Oprócz swojej późniejszej sławy jako wynalazcy trójramiennego kątomierza, zasugerował także stosowanie znaków wysokiej wody w londyńskich dokach, wciąż używanych do lat 60. XX wieku. Wynalazł napędzane parą urządzenia do produkcji lin, które wyznaczają standardy jakości przy produkcji lin. W 1916 r. Biuro Hydrograficzne Stanów Zjednoczonych wyjaśniło użycie swojego kątomierza: "Aby wykreślić pozycję, obserwowane są dwa kąty między trzema wybranymi [znanymi obiektami J ustawionymi na instrumencie, które następnie przesuwa się nad wykresem, aż trzy fazowane krawędzie przechodzą odpowiednio i jednocześnie przez trzy obiekty. Środek przyrządu zaznacza wówczas pozycję statku. który może zostać nakłuty na mapie lub zaznaczony ołówkiem przez środkowy otwór. "
Jean Baptiste Joseph Fourier (1768-1830)
Szeregi Fouriera są dziś przydatne w niezliczonych aplikacjach, od analizy drgań po przetwarzanie obrazu - praktycznie w każdym polu, w którym ważna jest analiza częstotliwości. Na przykład szereg Fouriera pomaga naukowcom scharakteryzować i lepiej zrozumieć skład chemiczny gwiazd lub sposób, w jaki układ głosowy wytwarza mowę. Zanim francuski matematyk Joseph Fourier odkrył swój słynny szereg, towarzyszył Napoleonowi w jego wyprawie do Egiptu w 1789 roku, gdzie Fourier spędził kilka lat studiując egipskie artefakty. Badania Fouriera nad matematyczną teorią ciepła rozpoczęły się około 1804 r., kiedy wrócił do Francji, a w 1807 r. ukończył swój ważny pamiętnik o propagacji ciepła w ciałach stałych. Jednym z jego zainteresowań była dyfuzja ciepła w różnych kształtach. W przypadku tych problemów badaczom zwykle podaje się temperatury w punktach na powierzchni, a także na jej krawędziach, w czasie t = 0. Fourier wprowadził serię z wyrazami sinus i cosinus w celu znalezienia rozwiązania tego rodzaju problemów. Mówiąc bardziej ogólnie, stwierdził, że dowolna funkcja różniczkowalna może być reprezentowana z dowolną dokładnością przez sumęfunkcji sinus i cosinus, bez względu na to, jak dziwnie może wyglądać funkcja po wykreśleniu. Biografowie Jerome Ravetz i I. Grattan-Guiness zauważają: "Osiągnięcie Fouriera można zrozumieć przez [rozważenie] potężnych narzędzi matematycznych, które wynalazł dla rozwiązań równań, które dały długą serię potomków i wywołały problemy w analizie matematycznej, które bardzo motywowały wiodących prac w tej dziedzinie przez resztę stulecia i później ". Brytyjski fizyk Sir James Jeans (1877-1946) zauważył: "Twierdzenie Fouriera mówi nam, że każda krzywa, bez względu na jej naturę, lub w jaki sposób został pierwotnie uzyskany, może być dokładnie odtworzony poprzez nałożenie wystarczającej liczby prostych krzywych harmonicznych - w skrócie, każdą krzywą można zbudować poprzez ułożenie fal ".
Pierre-Simon, markiz de Laplace (1749-1827)
Pierwszym ważnym traktatem o prawdopodobieństwie łączącym teorię prawdopodobieństwa i rachunek różniczkowy był francuski matematyk i astronom Pierre-Simon Laplace Theorie Analytique des Probabilites (Analytical Theory prawdopodobieństw). Teoretycy prawdopodobieństwa koncentrują się na zjawiskach losowych. Chociaż pojedynczy rzut kostką można uznać za zdarzenie losowe, po wielu powtórzeniach widoczne są pewne wzorce statystyczne, które można badać i wykorzystywać do prognozowania. Pierwsze wydanie Theorie Analytique Laplace'a było poświęcone Napoleonowi Bonaparte i omawia metody znajdowania prawdopodobieństw zdarzeń złożonych na podstawie prawdopodobieństw składowych. Książka omawia również metodę najmniejszych kwadratów i Igła Buffona i rozważa wiele praktycznych zastosowań. Stephen Hawking nazywa Theorie Analytique "arcydziełem" i pisze: "Laplace stwierdził, że ponieważ świat jest zdeterminowany, nie może być żadnych rzeczy. Prawdopodobieństwo skutkuje brakiem naszej wiedzy". Według Laplace'a nic nie byłoby "niepewne" dla wystarczająco zaawansowanego bytu - modelu konceptualnego, który pozostał silny aż do powstania mechaniki kwantowej i teorii chaosu w XX wieku. Aby wyjaśnić, w jaki sposób procesy probabilistyczne mogą dawać przewidywalne wyniki, Laplace prosi czytelników, aby wyobrazili sobie kilka urn ułożonych w CIrcle. Jedna urna zawiera tylko czarne kule, a druga zawiera tylko białe kule. Pozostałe urny mają różne mieszanki kulkowe. Jeśli wycofamy piłkę, umieścimy ją w sąsiedniej urnie i będziemy kontynuować koło, ostatecznie stosunek czarnych do białych kulek będzie w przybliżeniu taki sam we wszystkich urnach. Tutaj Laplace pokazuje, jak losowe "siły naturalne" mogą tworzyć wyniki o przewidywalności i porządku. Laplace pisze: "Zadziwiające jest to, że nauka, która powstała przy rozważaniu gier losowych, powinna stać się najważniejszym przedmiotem ludzkiej wiedzy. Najważniejsze pytania dotyczące życia są dla większości części, naprawdę tylko problemy prawdopodobieństwa. "Inni znani probabiliści to Gerolamo Cardano (1501-1576), Pierre de Fermat (1601-1665), Blaise Pascal (1623-1662) i Andriej Nikłajewicz Kołmogorow (1903-1987).
Książę Rupert z Renu (1619-1682), Pieter Nieuwland (1764-1794)
Problem księcia Ruperta ma długą i fascynującą historię. Książę Rupert był wynalazcą, artystą i żołnierzem. Biegle posługiwał się praktycznie wszystkimi głównymi językami europejskimi i znał doskonale matematykę. Żołnierze bali się dużego pudla, który zabierał ze sobą podczas bitew, wierząc, że ma nadprzyrodzone moce. W 1600 roku książę Rupert zadał słynne geometryczne pytanie: Jaki jest największy drewniany sześcian, który może przejść przez dany sześcian o boku długości jednego cala? A dokładniej, jaki jest rozmiar R krawędzi największego tunelu (o kwadratowym przekroju), który można wykonać przez sześcian bez jego łamania? Dziś wiemy, że odpowiedź to R = 3√2 / 4 = 1.060660…Innymi słowy, sześcian o długości boku R cala (lub mniejszej) może przejść przez sześcian o boku o długości I cala. Książę Rupert wygrał zakład, że można zrobić dziurę w jednym z dwóch jednakowych rozmiarów kostek wystarczająco dużych, aby drugi sześcian mógł się przez nie prześlizgnąć. Wielu uważało, że nie można tego osiągnąć. Chociaż pierwsza publikacja problemu księcia Ruperta została napisana przez Johna Wallisa (1616--1703) w jego 1685 De Algebra Tractatus, rozwiązanie 1.060660 nie było znany do chwili, gdy holenderski matematyk Pieter Nieuwland rozwiązał go ponad sto lat po tym, jak książę Rupert zadał to pytanie. Jego rozwiązanie zostało opublikowane pośmiertnie w 1816 r. przez jego nauczyciela Jana Hendrika van Swindena, który znalazł rozwiązanie Nieuwlanda wśród swoich prac. Jeśli trzymasz kostkę, tak aby jeden przybysz skierował się w twoją stronę, zobaczysz zwykły sześciokąt. Największy kwadrat, który przeciska się przez sześcian, ma powierzchnię, którą można wpisać w ten sześciokąt. Jak informują matematycy Richard Guy i Richard Nowakowski, największa kostka, która może przechodzić przez hipersześcian ma krawędź 1,007434775 … co jest pierwiastkiem kwadratowym z 1,014924 ..., najmniejszym pierwiastkiem z 4x4 - 283 - 7x2 + 16x + 16.
Friedrich Wilhelm Bessel (1784-1846)
Niemiecki matematyk Friedrich Bessel, który nie miał formalnego wykształcenia po ukończeniu 4 roku życia, rozwinął funkcje Bessela w 1817 r. Do wykorzystania w swoich badaniach ruchu planet poruszających się pod wzajemną grawitacją. Bessel uogólnił wcześniejsze ustalenia matematyka Daniela Bernoulli (1700-1782). Od czasu odkryć Bessela jego funkcje stały się niezbędnymi narzędziami w szerokim zakresie matematyki i inżynierii. Autor Boris Korenev pisał, "duża liczba różnorodnych problemów dotyczących praktycznie wszystkich najważniejszych dziedzin fizyki matematycznej i różnorodnych problemów technicznych związana jest z funkcjami Bessela. "Rzeczywiście, różne aspekty teorii funkcji Bessela są wykorzystywane przy rozwiązywaniu problemów związanych z przewodzeniem ciepła, hydrodynamiką , dyfuzja, przetwarzanie sygnałów, akustyka, fizyka radiowa i antenowa, wibracje płyt, oscylacje w łańcuchach, naprężenia, które ewoluują w pobliżu pęknięć materiałów, ogólnie propagacja fal oraz fizyka atomowa i jądrowa. W teorii elastyczności funkcje Bessela są przydatne do rozwiązywania licznych problemy przestrzenne wykorzystujące współrzędne sferyczne lub cylindryczne.
Funkcje Bessela są rozwiązaniami specyficznych równań różniczkowych, a po wykreśleniu funkcje przypominają falujące, zanikające fale sinusoidalne. Na przykład w przypadku równania falowego obejmującego okrągłą membranę, taką jak głowica bębna, jedna klasa rozwiązań obejmuje funkcje Bessela, a rozwiązanie fali stojącej można wyrazić jako funkcję Bessela, która jest funkcją odległości r od środka do krawędzi membrany. W 2006 r. Naukowcy z japońskiego Akishima Laboratories i Uniwersytetu w Osace oparli się na teorii funkcji Bessela, aby stworzyć urządzenie wykorzystujące fale do rysowania rzeczywistego tekstu i zdjęć na powierzchni wody. Urządzenie o nazwie AMOEBA (Advanced Multiple Organised Experimental Basin) składa się z 50 generatorów fal wodnych otaczających cylindryczny zbiornik o średnicy 1,6 metra i głębokości 30 cm. AMOEBA jest w stanie przeliterować cały alfabet rzymski. Każde zdjęcie lub litera pozostaje na powierzchni wody tylko przez chwilę, ale można je tworzyć kolejno co kilka sekund.
Charles Babbage (1792-1871), Augusta Ada King, hrabina Lovelace (1815-1852)
Charles Babbage był angielskim analitykiem, statystykiem i wynalazcą, który również interesował się tematem cudów religijnych. Kiedyś napisał: "Cuda nie są naruszeniem ustalonych praw, ale
wskazują na istnienie znacznie wyższych praw". Babbage argumentował, że cuda mogą wystąpić w mechanistycznym świecie. Tak jak Babbage mógł sobie wyobrazić programowanie dziwnych zachowań na swoich maszynach liczących, tak Bóg mógł programować podobne nieprawidłowości w naturze. Badając cuda biblijne, zasugerował, że szansa na powstanie człowieka z martwych wynosi 1 na 1012. Babbage jest często uważany za najważniejszego inżyniera matematyka zajmującego się prehistorią komputerów. W szczególności słynie z ogromnego, ręcznie obróconego mechanicznego kalkulatora, wczesnego przodka naszych współczesnych komputerów. Babbage myślał, że urządzenie będzie najbardziej przydatne w tworzeniu tabel matematycznych, ale martwił się błędami, które popełnialiby ludzie, którzy przepisywali wyniki z metalowych kół wyjściowych. Dziś zdajemy sobie sprawę, że Babbage wyprzedził swój wiek o około sto lat i że polityka i technologia jego epoki były nieodpowiednie dla jego wzniosłych marzeń. Silnik różnicowy Babbage'a, rozpoczęty w 1822 r., Ale nigdy nie ukończony, został zaprojektowany do obliczania wartości funkcji wielomianowych przy użyciu około 25 000 części mechanicznych. Miał też plany stworzenia bardziej ogólnego komputera, silnika analitycznego, który mógłby być programowany przy użyciu kart dziurkacza i miał osobne obszary do przechowywania liczb i obliczeń. Esllmates sugeruje, że silnik analityczny zdolny do przechowywania 1000 liczb 50-cyfrowych miałby długość ponad 100 stóp (około 30 metrów). Ada Lovelace, córka angielskiego poety Lorda Byrona, podała specyfikacje programu dla silnika analitycznego. Chociaż Babbage udzielał pomocy Adzie, wielu uważa, że Ady jest pierwszym programistą komputerowym. W 1990 roku powieściopisarze William Gibson i Bruce Sterling napisali The Difference Engine, w którym poprosili czytelników o wyobrażenie sobie konsekwencji mechanicznych komputerów Babbage'a dla społeczeństwa wiktoriańskiego.
Augustin Louis Cauchy (1789-1857)
Amerykański matematyk William Waterhouse pisze: "Rachunek w 1800 roku był w dziwnym stanie. Nie było wątpliwości, że było poprawne. Matematycy o wystarczających umiejętnościach i wnikliwości odnieśli sukces od stu lat. Jednak nikt nie potrafił jasno wyjaśnić, dlaczego to zadziałało
.. Potem przyszedł Cauchy. " W swoim życiorysie "Resume des lefons sur Ie calcul infinitesimal" (Resume of Lessons on Infinitesimal Calculus) płodny matematyk Augustin Cauchy przedstawia rygorystyczny rozwój rachunku różniczkowego i współczesnego dowodu na podstawowe twierdzenie rachunku różniczkowego, które elegancko łączy dwie główne gałęzie rachunku rachunek różniczkowy (różniczkowy i całkowy) w jednej strukturze. Cauchy zaczyna swój traktat od jasnej definicji pochodnej. Jego mentor, Francuski matematyk Joseph-Louis Lagrange (1736-1813) zastanawiał się nad wykresami krzywych i uważał pochodną za styczną do krzywej. Aby ustalić pochodną, Lagrange szukał wzorów pochodnych w razie potrzeby. Stephen Hawking pisze: "Cauchy wykroczył daleko poza Lagrange'a i zdefiniował pochodną f przy x jako granica ilorazu różnicy Δy/Δx = [f(x+1) - f(x)]/i", gdy i zbliża się do zera, co jest naszą współczesną, niegeometryczną definicją pochodnej. Podobnie przez wyjaśnienie pojęcia całka w rachunku całkowym, Cauchy wykazał Podstawowe Twierdzenie Rachunku, które ustanawia sposób, w jaki możemy obliczyć całkę f(x) od x = a do x = b dla dowolnej funkcji ciągłej f. W szczególności, Podstawowe Twierdzenie Rachunku stwierdza, że jeśli f jest funkcją całkowitą w przedziale [a, b], a jeśli H(x) jest całką f{x) od a do x ≤ b, to pochodna H(x) jest identyczna z f(x). Innymi słowy, H′ (x) = f(x). Waterhouse konkluduje: "Cauchy tak naprawdę nie założył nowych fundacji; zmiótł cały kurz, aby odsłonić cały gmach kamienia, który już stał na skale. ... "
August Ferdinand Möbius (1790-1868)
Niemiecki matematyk August Ferdinand Möbius, znany ze swojej jednostronnej pętli zwanej pasmem Mobiusa, również wniósł duży wkład w matematykę za pomocą rachunku barycentrycznego, geometrycznej metody określania punktu jako środka ciężkości niektórych innych punktów, dla których współczynniki lub wagi są przypisane. Możemy myśleć o współrzędnych barycentrycznych Mobiusa (lub środkowych) jako współrzędnych w odniesieniu do trójkąta odniesienia. Współrzędne te są zwykle zapisywane jako trzykrotne liczby, które można wizualizować jako odpowiadające masom umieszczonym na wierzchołkach trójkąta. W ten sposób masy te określają punkt, który jest geometrycznym środkiem masy trzech mas. Nowe narzędzia algebraiczne, opracowane przez Mobiusa w jego książce z 1827 r. Der Barycentrische Calcul (The Barycentric Calculus), od tego czasu mają szerokie zastosowanie. Ta klasyczna książka również omawia powiązane tematy w geometrii analitycznej, takie jak transformacje rzutowe. Słowo barycentryczny pochodzi od greckiego słowa "ciężki" i odnosi się do środka masy. Möbius zrozumiał, że kilka ciężarków ustawionych wzdłuż prostego drążka można zastąpić pojedynczym ciężarem w środku masy drążka. Na podstawie tej prostej zasady skonstruował system matematyczny, w którym współczynniki numeryczne są przypisane do każdego punktu w przestrzeni. Współrzędne barycentryczne są dziś traktowane jako forma współrzędnych ogólnych, które są stosowane w wielu gałęziach matematyki i grafice komputerowej. Wiele zalet współrzędnych barycentrycznych występuje w dziedzinie geometrii rzutowej, która dotyczy incydentów - to znaczy, gdy elementy takie jak linie, płaszczyzny i punkty albo się pokrywają, albo nie. Geometria rzutowa dotyczy również relacji między obiektami i odwzorowaniami, które wynikają z rzutowania obiektów na inną powierzchnię, którą można zwizualizować jako cienie obiektów stałych.
Nikołaj Iwanowicz Łobaczewski (1792-1856), Janos Bolyai (l802-1860), Georg Friedrich Bernhard Riemann (l826-1866)
Od czasów Euklidesa (ok. 325-270 p.n.e.) tak zwany postulat równoległy wydawał się rozsądnie opisywany, jak działa nasz trójwymiarowy świat. Zgodnie z tym postulatem, biorąc pod uwagę linię prostą i punkt nie na tej linii, istnieje tylko jedna linia prosta przechodząca przez punkt, który nigdy nie przecina linii pierwotnej. Z biegiem czasu sformułowania geometrii nieeuklidesowej, w których ten postulat się nie utrzymuje, miały dramatyczne konsekwencje. Einstein powiedział o geometrii innej niż euklidesowa: "Do tej interpretacji geometrii przywiązuję wielką wagę, ponieważ gdybym się z nią nie zapoznał, nigdy nie byłbym w stanie rozwinąć teorii względności". W rzeczywistości. Ogólna teoria względności Einsteina reprezentuje czasoprzestrzeń jako geometrię nieeuklidesową, w której czasoprzestrzeń faktycznie wypacza się lub wygina w pobliżu ciał grawitacyjnych, takich jak słońce i planety. Można to zobrazować wyobrażając sobie, jak kula do kręgli tonie w gumowym prześcieradle. Jeśli umieścisz marmur w zagłębieniu utworzonym przez rozciągnięty arkusz gumy i popchniesz marmur na boki, to krąży on przez chwilę na kuli do kręgli, jak planeta krążąca wokół Słońca. W 1829 r. rosyjski matematyk Mikołaj Łobaczewski opublikował O zasadach geometrii, w którym wyobrażał sobie idealnie spójną geometrię wynikającą z założenia, że równoległy postulat jest fałszywy. Kilka lat wcześniej węgierski matematyk Janos Bolyai pracował nad podobną nieeuklidesową geometrią, ale jego publikacja została opóźniona do 1932 r. W 1854 r. Niemiecki matematyk Bernhard Riemann uogólnił ustalenia Bolyaia i Łobaczewskiego, pokazując, że możliwe są różne geometrie nieeuklidesowe , biorąc pod uwagę odpowiednią liczbę wymiarów. Riemann zauważył kiedyś: "Wartość geometrii nieeuklidesowej polega na jej zdolności do wyzwolenia nas z uprzednio przyjętych pomysłów w przygotowaniu na czas, gdy eksploracja praw fizycznych może wymagać geometrii innej niż euklidesowa". Jego przewidywania zrealizowano później za pomocą ogólnej teorii względności Einsteina.
August Ferdinand Möbius (1790-1868)
W 1831 r. August Möbius wprowadził swoją egzotyczną funkcję Möbiusa, dziś zapisaną jako μ(n). Aby zrozumieć tę funkcję, wyobraź sobie umieszczenie wszystkich liczb całkowitych w jednej z trzech dużych skrzynek pocztowych. Pierwsza skrzynka pocztowa jest pomalowana dużą cyfrą "0", druga cyfrą "+1." i trzecią cyfrą "-1". W skrzynce pocztowej 0 Möbius umieszcza wielokrotności liczb kwadratowych (innych niż 1), w tym (4, 8 ,9 , 12 , 16, 18 …). Liczba kwadratowa to liczba taka jak 4,9 lub 16, która jest kwadratem innej liczby całkowitej. Na przykład μ(12) = 0, ponieważ 12 jest wielokrotnością liczby kwadratowej 4 i dlatego jest umieszczana w skrzynce pocztowej "0". W skrzynce pocztowej -1 Möbius umieszcza dowolną liczbę, która uwzględnia nieparzystą liczbę różnych liczb pierwszych liczb. Na przykład 5 x 2 x 3 = 30, więc 30 znajduje się na tej liście, ponieważ ma te trzy czynniki pierwsze. Wszystkie liczby pierwsze również znajdują się na tej liście, ponieważ same mają tylko
jeden czynnik pierwszy. Zatem μ( 29) = -1 i μ(30) = -1. Prawdopodobieństwo, że liczba spadnie do skrzynki pocztowej -1 okazuje się równe 3/π2 - to samo prawdopodobieństwo, co do wpadnięcia do skrzynki pocztowej +1. Przejdźmy dalej do skrzynki pocztowej +1 , w której Möbius umieszcza wszystkie liczby , takie jak 6, ten czynnik w parzystej liczbie różnych liczb pierwszych (2 x 3 = 6). Dla kompletności Möbius umieścił 1 na tym pojemniku. Liczby w tej skrzynce pocztowej obejmują (1, 6, 10, 14, IS, 21,22, …). Pierwszych 20 terminów cudownej funkcji Möbiusa to μ(n) = {1, - 1, - 1, 0, -1, 1, -1, 0 ,0, 1, -1, 0, -1, 1, 1,0, -1,0, -1,0} . Dziwnie, naukowcy znaleźli praktyczne zastosowania funkcji Möbiusa w różnych fizycznych interpretacjach teorii cząstek subatomowych. Funkcja Möbiusa jest również fascynująca, ponieważ prawie wszystko w jej zachowaniu jest nierozwiązane i ponieważ istnieje wiele eleganckich matematycznych tożsamości, które obejmują μ(n).
Evariste Galois (1811-1832)
Francuski matematyk Evariste Calois był odpowiedzialny za teorię Galois, ważną gałąź algebry abstrakcyjnej, i słynął z wkładu w teorię grup, która dotyczy matematycznego badania symetrii. W szczególności w 1832 r. Opracował metodę określania, kiedy ogólne równanie może zostać rozwiązane przez rodniki, tym samym w istocie. dając początek nowoczesnej teorii grup Martin Cardner pisze: "W 1832 r. został zabity strzałem z pistoletu. Nie miał jeszcze 21 lat. Pewne wczesne fragmentaryczne prace wykonano na grupach, ale to Galois stworzył podstawy współczesnej teorii grup i nawet nazwał to, wszystko w długim, smutnym liście, który napisał do przyjaciela w noc poprzedzającą jego pojedynek pistoletowy ". Jednym kluczowym aspektem grupy jest to, że jest to zestaw elementów z operacją, która łączy dowolne dwa jej elementy, tworząc trzeci element w tym zestawie. Weźmy na przykład zestaw liczb całkowitych i operację dodawania, które razem tworzą grupę. Dodanie dwóch liczb całkowitych zawsze daje liczbę całkowitą. Obiekt geometryczny można scharakteryzować za pomocą grupy zwanej grupą symetrii, która określa cechy symetrii obiektu. Ta grupa zawiera zestaw transformacji, które pozostawiają obiekt bez zmian po zastosowaniu. Dzisiaj ważne tematy teorii grup są często ilustrowane uczniom używającym Kostki Rubika. Okoliczności, które doprowadziły do śmierci Calois, nigdy nie zostały w pełni wyjaśnione. Być może jego śmierć wynikła z kłótni o kobietę lub z powodów politycznych. W każdym razie, przygotowując się do końca, spędził noc gorączkowo opisując swoje matematyczne pomysły i "odkrycia". Następnego dnia Calois został trafiony w brzuch. Leżał bezradnie na ziemi. Nie było lekarza, który by mu pomógł, a zwycięzca od niechcenia odszedł, zostawiając Calois wić się w agonii. Jego matematyczna reputacja i dziedzictwo spoczywa na mniej niż 100 stronach genialnie opublikowanego pośmiertnie dzieła.
Johann Peter Gustav Lejeune Dirichlet (1805-1859)
Pierwsze oświadczenie o Zasadzie Szufladki zostało wypowiedziane przez niemieckiego matematyka Johanna Dirichleta w 1834 r., Chociaż nazwał je Schubfachprinzip ("Zasada szuflady"). Wyrażenie "Zasada Szuflady" zostało po raz pierwszy użyte w poważnym czasopiśmie matematycznym przez matematyka Raphaela M. Robinsona w 1940. Mówiąc wprost, jeśli mamy m gołębników i n gołębi, możemy być pewni, że co najmniej jeden gołębnik ma więcej niż jednego gołębia, jeśli n > m. To proste stwierdzenie zostało zastosowane w aplikacjach, od kompresji danych komputerowych po problemy obejmujące nieskończone zestawy, których nie można umieścić w korespondencji jeden do jednego. Zasada Szuflady została również uogólniona do zastosowań probabilistycznych, dzięki czemu jeśli n gołębi zostanie losowo umieszczonych w m szufladach z jednakowym prawdopodobieństwem 1/m, to co najmniej jedna szuflada pomieści więcej niż jednego gołębia z prawdopodobieństwem 1- m!/ [(m - n )!mn]. Rozważmy kilka przykładów, które mogą wykazywać nieintuicyjne wyniki. Z powodu zasady szuflady, w Nowym Jorku muszą być co najmniej dwie osoby z taką samą liczbą włosów na głowie. Niech włosy będą reprezentowane jako szuflady, a ludzie jak gołębie. Miasto Nowy Jork ma ponad 8 milionów ludzi, a ludzka głowa ma znacznie mniej niż milion włosów; dlatego co najmniej dwie osoby muszą istnieć z taką samą liczbą włosów na głowie. Papier o wymiarach banknotu dolarowego ma kolor niebieski i czerwony na jednej powierzchni. Czy zawsze można znaleźć dwa punkty tego samego koloru w odległości dokładnie jednego cala od siebie na takiej powierzchni, bez względu na to, jak misternie zabarwiona jest powierzchnia? Aby rozwiązać, narysuj trójkąt równoboczny o krawędziach 1 cala. Traktuj kolory jak szuflady, a wierzchołki trójkąta jak gołębie. Co najmniej dwa z jego wierzchołków muszą być tego samego koloru. Dowodzi to, że dwa punkty tego samego koloru muszą istnieć dokładnie w odległości jednego cala.
Sir William Rowan Hamilton (1805-1865)
Kwaterniony są liczbami czterowymiarowymi opracowanymi w 1843 r. przez irlandzkiego matematyka Williama Hamiltona. Od tego czasu kwaterniony są używane do opisania dynamiki ruchu w trzech wymiarach i stosowane w takich dziedzinach, jak grafika komputerowa do rzeczywistości wirtualnej, programowanie gier wideo, przetwarzanie sygnałów, robotyka, bioinformatyka i badania geometrii czasoprzestrzeni. Oprogramowanie lotu promu kosmicznego wykorzystuje kwaterniony do obliczeń nawigacji, nawigacji i kontroli wysokości, ze względu na szybkość, zwartość i niezawodność. Pomimo potencjalnej użyteczności kwaternionów, niektórzy matematycy byli początkowo sceptyczni. Szkocki fizyk William Thomson (1824-1907) napisał: "Kwaterniony przybyły od Hamiltona po tym, jak jego naprawdę dobra robota została wykonana, i choć pięknie pomysłowe, były niezmieszanym złem dla tych, którzy ich w jakikolwiek sposób dotknęli". Z drugiej strony, inżynier i matematyk Oliver Heaviside napisał w 1892 roku: "Wynalazek kwaternionów należy uznać za najbardziej niezwykły wyczyn ludzkiej pomysłowości. Analizy wektorowe, bez kwaternionów, każdy matematyk mógłby znaleźć ... nasze kwaterniony przerodziły się w geniusz". Co ciekawe, Theodore Kaczyński ("Unabomber") napisał skomplikowane traktaty matematyczne o kwaternionach, zanim zaczął szaleństwo zabijania. Kwartiony mogą być reprezentowane w czterech wymiarach przez Q = a0 + a1i + a2j + a3k, gdzie i, j oraz k są (podobnie jak liczba urojona i) wektorami jednostkowymi w trzech ortogonalnych (prostopadłych) kierunkach i są one prostopadłe do osi liczb rzeczywistych. Aby dodać lub pomnożyć dwa kwaterniony, traktujemy je jako wielomiany w i, i i k, ale stosujemy następujące reguły do obsługi iloczynów : i2 = j2 =k2 = -1 ; ij = - ji = k; jk = - kj = i; i ki = -ik = j. Hamilton mówi nam, że pokroił te formuły w kamień mostu Brougham w Dublinie, idąc razem z żoną, po tym, jak pomysły pojawiły się w mgnieniu oka.
Joseph Liouville (1809-1882), Charles Hermite (1822-1901), Ferdynand von Lindemann (1852-1939)
W 1844 roku francuski matematyk Joseph Liouville rozważył następującą interesującą liczbę: 0.110001000000000000000001000 …, znaną dziś jako stała Liouville. Czy potrafisz odgadnąć jego znaczenie lub jaką zasadę stworzył? Liouville wykazał, że jego niezwykła liczba była transcendentalna, co czyni tę liczbę jedną z pierwszych, która została udowodniona, transcendentalną. Zauważ, że stała ma 1 w każdym miejscu dziesiętnym odpowiadające silni, a zera gdzie indziej. Oznacza to, że 1-nki występuje tylko w 1-szym, 2-gim, 6-tym, 24-tym, 120-tym, 720-tym, itd. miejscu. Liczby transcendentalne są tak egzotyczne, że zostały "odkryte" stosunkowo niedawno w historii i być może znasz tylko jeden z nich, π, a być może liczba Eulera, np. Liczb tych nie można wyrazić jako pierwiastek żadnego równania algebraicznego o współczynnikach wymiernych. Oznacza to na przykład, że π nie może dokładnie spełnić równań takich jak 2x4 - 3x2 + 7 = 0. Trudne jest udowodnienie, że liczba jest transcendentalna. Francuski matematyk Charles Hermite udowodnił, że e jest transcendentalny w 1873 r., a niemiecki matematyk Ferdinand von Lindemann udowodnił, że π był transcendentalne w 1882 r. W 1874 r. niemiecki matematyk Georg Cantor zaskoczył wielu matematyków, wykazując, że "prawie wszystkie" liczby rzeczywiste są transcendentalne. Tak więc, jeśli potrafisz jakoś włożyć wszystkie liczby do dużego słoika, potrząsnąć słojem i wyciągnąć jedną, byłoby praktycznie pewne, że jest transcendentalna. Jednak pomimo faktu, że liczby transcendentalne są "wszędzie", tylko kilka jest znanych i nazwanych. Na niebie jest wiele gwiazd, ale ile możesz wymienić? Oprócz zajęć matematycznych Liouville interesował się polityką i został wybrany do francuskiego zgromadzenia konstytucyjnego w 1848 r. Po późniejszej porażce wyborczej Liouville popadł w depresję. Jego matematyczne wędrówki przeplatały poetyckie cytaty. Niemniej jednak w ciągu swojego życia Liouville napisał ponad 400 poważnych prac matematycznych.
Eugene Charles Catalan (1814-1894), Preda Mihailescu (ur. 1955)
Zwodniczo proste wyzwania z udziałem liczb całkowitych mogą wprawić w zakłopotanie nawet najbardziej błyskotliwych matematyków. Tak jak w przypadku ostatniego twierdzenia Fermata, mogą minąć stulecia, zanim proste domysły dotyczące liczb całkowitych zostaną udowodnione lub obalone. Niektóre problemy mogą nigdy nie zostać rozwiązane, nawet przy połączonym wysiłku ludzi i komputerów.
Aby przygotować scenę dla zrozumienia przypuszczenia Catalana, rozważ kwadraty liczb całkowitych (liczb całkowitych) większe niż 1, to znaczy 4, 9,16,25, ... a także rozważ kolejność kostek, 8, 27, 64 , 125 .... po połączeniu dwóch list i uporządkowaniu ich, otrzymujemy 4,8,9, 16,25,27, 36, .... Zauważ, że 8 (sześcian 2) i 9 ( kwadrat z 3) są kolejnymi liczbami całkowitymi. W 1844 r. Belgijski matematyk Eugene Catalan przypuszczał, że 8 i 9 są jedynymi potęgami liczb całkowitych następujących po sobie! Gdyby istniały inne takie pary, można by je znaleźć, szukając wartości całkowitych, dla których xp - yq = 1 jest prawdziwe, oraz wartości x, y, p i q są większe niż 1. Catalan wierzył, że istnieje tylko jedno rozwiązanie: 32 - 23= 1 . Ta historia przypuszczenia Catalana ma barwną obsadę postaci. Setki lat przed Catalanem Francuz Levi ben Gerson (1288-1 344) - lepiej znany jako Gersonides lub Ralbag- wykazali już bardziej ograniczoną wersję przypuszczenia, mianowicie, że jedynymi potęgami 2 i 3, które różnią się między mną, są 32 i 23 Ralbag był znanym rabinem, filozofem, matematykiem i talmudystą. Przejdźmy do 1976 roku, kiedy Robert Tijdeman z University of Leiden w Holandii wykazał, że gdyby istniały przykłady innych następujących po sobie potęg, to musiałyby one być skończone. Wreszcie w 2002 roku Preda Mihailescu z Uniwersytetu w Paderbom w Niemczech udowodniła przypuszczenie Catalana.
James Joseph Sylvester (1814-1897), Arthur Cayley (1821-1895)
W 1850 r. Brytyjski matematyk James Sylvester w swojej pracy "O nowej klasie twierdzeń" jako pierwszy użył słowa macierz, odnosząc się do prostokątnego układu lub tablicy elementów, które można dodawać i mnożyć. Macierze są często używane do opisania układu równań liniowych lub po prostu do przedstawienia informacji zależnej od dwóch lub więcej parametrów. Uznanie za zaniżenie i zidentyfikowanie pełnego znaczenia właściwości algebraicznych macierzy przypisuje angielski matematyk Arthur Cayley za późniejszą pracę nad macierzami w 1855 r. Ponieważ Cayley i Sylvester cieszyli się wieloletnią bliską współpracą, często są uważani za wspólnych założycieli teorii macierzy. Chociaż teoria macierzy rozkwitła w połowie XIX wieku, proste koncepcje macierzy sięgają czasów przed narodzinami Chrystusa, kiedy Chińczycy znali Magiczne kwadraty, a także zaczęli stosować metody macierzowe do rozwiązywania równań. W XVI wieku japoński matematyk Seki Kowa (w 1683 r.) I niemiecki matematyk Gottfried Leibniz (w 1693 r.) Również zapoznali się z wczesnym użyciem macierzy. Zarówno Sylvester, jak i Cayley studiowali w Cambridge, ale Sylvester nie kwalifikował się do uzyskania dyplomu, ponieważ był Żydem, chociaż zajął drugie miejsce w egzaminach matematycznych Cambridge. Przed Cambridge. Sylvester uczęszczał do Royal Institution w Liverpoolu, gdzie studenci dręczyli go za swoją religię, co spowodowało, że uciekł do Dublina. Cayley pracował jako prawnik przez ponad dekadę, publikując około 250 artykułów matematycznych. Podczas swojego pobytu w Cambridge opublikował kolejne 650 artykułów. Cayley jako pierwszy wprowadził mnożenie macierzy. Obecnie matryce stosuje się w wielu obszarach, w tym do szyfrowania i deszyfrowania danych, manipulacji obiektami w grafice komputerowej (w tym gier wideo i obrazowania medycznego), rozwiązywania układów równań liniowych, kwantowo-mechanicznych badań struktury atomowej, równowagi ciał sztywnych w fizyce, teoria grafów, teoria gier, modele ekonomiczne i sieci elektryczne.
Francis Guthrie (1831-1899), Kenneth Appel (1932-2013), Wolfgang Haken (ur. 1928)
Twórcy map wierzyli przez wieki, że tylko cztery kolory wystarczają do pokolorowania dowolnej mapy narysowanej na płaszczyźnie, tak że żadne dwa odrębne regiony o wspólnej krawędzi nie są tego samego koloru, chociaż dwa regiony mogą mieć wspólny wierzchołek i mieć ten sam kolor. Dziś wiemy na pewno, że choć niektóre mapy planarne wymagają mniej kolorów, żadna mapa nie wymaga więcej niż czterech. Cztery kolory są wystarczające dla map narysowanych na kulach i walcach. Siedem kolorów wystarcza do namalowania dowolnej mapy na torusie (na powierzchni kształtu pączka). W 1852 r. Matematyk i botanik Francis Guthrie jako pierwszy domyślił się, że cztery kolory muszą wystarczyć, gdy próbował pokolorować mapę hrabstw Anglii. Od czasów Guthrie matematycy na próżno próbowali udowodnić konsekwencje tej pozornie prostej czterokolorowej obserwacji, która pozostała jednym z najbardziej nierozwiązanych problemów w topologii. Wreszcie w 1976 r. Matematykom Kennethowi Appelowi i Wolfgangowi Hakcnowi udało się udowodnić czterokolorowe twierdzenie za pomocą komputera testującego tysiące przypadków, co sprawia, że pierwszym problemem w czystej matematyce jest użycie komputera do stworzenia niezbędnego komponentu dla dowód. Obecnie komputery odgrywają coraz większą rolę w matematyce, pomagając matematykom weryfikować dowody tak skomplikowane, że czasami przeciwstawiają się ludzkiemu zrozumieniu. Twierdzenie o czterech kolorach jest jednym przykładem. Kolejnym jest klasyfikacja skończonych prostych grup zawartych w 10 000-stronicowym projekcie wieloautorskim. Niestety, źle ukierunkowane na ludzi metody zapewniania poprawności dowodu psują się, gdy papier dociera do tysięcy stron. Co zaskakujące, czterokolorowe twierdzenie ma często praktyczne znaczenie dla twórców map i kartografów. Na przykład badanie atlasów w czasie ujawnia brak pilnej chęci zminimalizowania liczby używanych kolorów, a książki o kartografii i historii tworzenia map często używają więcej kolorów, niż jest to konieczne
George Boole (1815-1864)
Najważniejszym dziełem angielskiego matematyka George'a Boole'a było jego opracowanie w 1854 r. "Dochodzenie w sprawie praw myśli, na których oparte są matematyczne teorie logiki i prawdopodobieństw". Boole był zainteresowany zredukowaniem logiki do prostej algebry obejmującej tylko dwie wielkości, 0 i 1 oraz trzy podstawowe operacje: i, lub, i nie. W czasach współczesnych algebra Boolean ma szerokie zastosowanie w przełączaniu telefonów i projektowaniu modemów komputerowych. Boole postrzegał to dzieło jako "najcenniejszy ... wkład, który wniosłem lub prawdopodobnie wniosę w naukę, oraz rzecz, którą chciałbym, aby w ogóle został zapamiętany później ...... Niestety, Boole zmarł w wieku 49 lat po tym, jak dostał silnej gorączki. Niestety jego żona uznała, że lekarstwo powinno przypominać przyczynę, a ona wylała na niego wiadra z zimną wodą, gdy leżał w łóżku, ponieważ jego choroba została przyspieszona przez przebywanie na zewnątrz zimny deszcz. Matematyk August De Morgan (1806-187) pochwalił jego pracę, mówiąc: "System logiki Boole'a jest tylko jednym z wielu dowodów genialności i cierpliwości połączonych
Że symboliczne procesy algebry, wymyślone jako narzędzia obliczenia numeryczne powinny być kompetentne do wyrażania każdego aktu myślenia oraz do dostarczania gramatyki i słownika wszechstronnego systemu logiki, nie uwierzyłyby, dopóki nie zostanie udowodnione ...". Około siedemdziesiąt lat po śmierci Boole'a, Amerykański matematyk Claude Shannon (1916-2001) został wprowadzony do algebry Boolean, gdy był jeszcze studentem, i pokazał, jak można użyć algebry Boolean do optymalizacji projektowania systemów przełączników routingu telefonicznego. Wykazał również, że obwody z przekaźnikami mogą rozwiązać problemy algebry logicznej. Tak więc Boole, z pomocą Shannona, stanowił jeden z fundamentów naszej epoki cyfrowej.
Sir William Rowan Hamilton (1805-1865)
W 1857 r. Irlandzki matematyk, fizyk i astronom William Hamilton opisał grę Icosian, której celem jest znalezienie ścieżki wzdłuż krawędzi dwunastościanu (wielościanu z 12 ściankami), aby każdy wierzchołek (przybysz) był odwiedzany tylko raz . Dziś w dziedzinie teorii grafów matematycy odnoszą się do ścieżki hamiltonowskiej jako takie, w którym ścieżka odwiedza każdy wierzchołek wykresu dokładnie raz. Cykl hamiltonowski (lub obwód hamiltonowski) wymagany dla gry Icosian oznacza, że ścieżka wraca do punktu początkowego. Brytyjski matematyk Thomas Kirkman (1806-1895) postawił problem gry Icosian bardziej ogólnie: czy na podstawie wykresu wielościanu istnieje cykl, który przebiega przez każdy wierzchołek? Termin lcosian pochodzi od wynalazku Hamiltona pewnego rodzaju algebry zwanej rachunkiem lcosian, opartym na właściwościach symetrii dwudziestościanu. Rozwiązał swoją łamigłówkę za pomocą tej algebry i powiązanych z nią icosians (specjalne rodzaje wektorów). Wszystkie platońskie ciała stałe są hamiltonowskie. W 1974 roku matematyk Frank Rubin opisał skuteczną procedurę wyszukiwania, która może znaleźć niektóre lub wszystkie ścieżki i obwody Hamiltona na wykresach. Londyński producent zabawek kupił prawa do gry Icosian i stworzył układankę z gwoździami na każdym wierzchołku dwunastościanu. Każdy gwóźdź oznaczał duże miasto. Gracz wytyczył swoją ścieżkę, owijając sznurek wokół każdego gwoździa podczas podróży. Zabawka była również sprzedawana w innych formach - na przykład jako płaska tablica z otworami w węzłach dwunastościanu. (Płaski model dwunastościanu można stworzyć, nakłuwając jeden z jego wybiegów i rozciągając go na płasko, tak aby leżał na płaszczyźnie). Niestety, gra nie sprzedała się dobrze, częściowo dlatego, że była wyjątkowo łatwa do rozwiązania. Być może skupienie się Hamiltona na głębokich teoriach zmusiło go do przeoczenia faktu, że próby i błędy wkrótce doprowadzą do rozwiązania!
Jules Antoine Lissajous (1822-1880), Hugh Blackburn (1823-1909)
Hannonograf jest wiktoriańskim urządzeniem artystycznym, które zwykle wykorzystuje tylko dwa wahadła, aby wyznaczyć ścieżki, które można badać zarówno z perspektywy artystycznej, jak i matematycznej. W jednej wersji wahadło porusza długopis. Drugie wahadło przesuwa stół z kartką papieru. Połączony efekt dwóch wahadeł wytwarza skomplikowany ruch, który z powodu tarcia stopniowo zanika do jednego punktu. Każda ścieżka pióra, po każdym obrocie, znajduje się w niewielkiej odległości od ścieżki poprzedniego obrotu, nadając wzorom falisty, przypominający pajęczynę wygląd. Zmieniając względem siebie częstotliwość i fazy wahadła, generowany jest szeroki zakres wzorów. W najprostszej wersji wzory można scharakteryzować jako krzywe Lissajous, które opisują złożony ruch hannonowy i mogą być reprezentowane (przy założeniu braku tarcia) przez krzywe wytworzone przez x(t) = Asin(at + d), y(t) = Bsin(bt), gdzie t jest czasem, a A i B są amplitudami . Stosunek a do b kontroluje częstotliwości względne, a d jest różnicą faz. Ze stosunkowo niewielu parametrów powstaje ogromna liczba ozdobnych krzywych. Pierwsze harmonografy skonstruowano w 1857 r., Kiedy francuski matematyk i fizyk Jules Antoine Lissajous zademonstrował wzory wytwarzane przez dwa kamertony, przymocowane do małych zwierciadeł, które wibrowały przy różnych częstotliwościach. Wiązka światła odbijała się od luster, tworząc skomplikowane zakręty, które zachwycały ogół społeczeństwa. Brytyjskiemu matematykowi i fizykowi, Hugh Blackburnowi, przypisuje się tworzenie najbardziej tradycyjnych wahadłowych wersji harmonografu, a do dziś powstało wiele odmian hannonografów Blackburna. Bardziej złożone harmonografy mogą wykorzystywać dodatkowe wahadła, które się ze sobą zwisają. W mojej powieści The Heaven Virus napotykamy zwariowanego hannonografa obcych z "piórem, który oscyluje na platformie, która oscylowała na innej platformie, która oscylowała na innej platformie, i tak dalej dla dziesięciu różnych platform".
August Ferdinand Möbius (1790--1868)
Niemiecki matematyk August Ferdinand Möbius był nieśmiałym, nietowarzyskim, roztargnionym profesorem, którego najsłynniejszego odkrycia, wstęga Möbiusa, dokonano, gdy miał prawie siedemdziesiąt lat. Aby samodzielnie utworzyć pasek, po prostu połącz dwa końce wstążki dając jeden koniec skrętnie o 180 stopni w stosunku do drugiego końca. Rezultatem jest powierzchnia jednostronna - robak może czołgać się z dowolnego punktu na takiej powierzchni do dowolnego innego punktu bez przekraczania krawędzi. Spróbuj pokolorować pasek Möbiusa kredką. Nie można pokolorować jednej strony na czerwono, a drugą na zielono, ponieważ pasek ma tylko jedną stronę. Wiele lat po śmierci Möbiusa wzrosła popularność i zastosowania paska, i to on stał się integralną częścią matematyki, magii, nauki, sztuki, inżynierii, literatury i muzyki. Pasek Möbius jest wszechobecnym symbolem recyklingu, gdzie reprezentuje proces przekształcania odpadów w przydatne zasoby. Dziś wstęga Möbiusa jest wszędzie, od cząsteczek i metalowych rzeźb po znaczki pocztowe, literaturę, patenty technologiczne, struktury architektoniczne i modele całego naszego wszechświata. August Möbius jednocześnie odkrył swój słynny pas ze współczesnym uczonym, niemieckim matematykiem Johannem Benedictem Listingiem (1808--1882). Wydaje się jednak, że Möbius posunął tę koncepcję nieco dalej niż Listing, ponieważ Möbius bliżej zbadał niektóre z niezwykłych właściwości tego paska. Pasek Möbiusa to pierwsza jednostronna powierzchnia odkryta i zbadana przez ludzi. Wydaje się zbyt daleko posunięte, że nikt nie opisał właściwości powierzchni jednostronnych do połowy XIX wieku, ale historia nie odnotowała takich obserwacji. Biorąc pod uwagę, że pasek Möbiusa jest często pierwszą i jedyną ekspozycją szerokiej publiczności na badania topologii - nauki o kształtach geometrycznych i ich relacjach
Hamnet Holditch (1800-1867)
Narysuj gładką, zamkniętą, wypukłą krzywą C1. Umieść cięciwę o stałej długości wewnątrz krzywej C1 i pozwól, aby cięciwa przesunęła się wewnątrz krzywej, tak aby dwa końce cięciwy zawsze dotykały C1. (Można to sobie wyobrazić jako przesuwanie drążka po powierzchni kałuży, która ma kształt krzywej C1) Oznacz punkt na drążku, aby podzielił drążek na dwie części długości p i q. Podczas przesuwania drążka punkt kreśli nową zamkniętą krzywą Cz2 w pierwotnej krzywej. Zakładając, że C1 jest ukształtowany w taki sposób, że drążek może faktycznie ominąć C1 raz, twierdzenie Holditcha stwierdza, że obszar między krzywymi C1 i C2 "niech będzie πpq. Co ciekawe, obszar ten jest całkowicie niezależny od kształtu C1 Matematycy zachwycali się twierdzeniem Holditcha od ponad stu lat. Na przykład w 1988 r. Brytyjski matematyk Mark Cooker napisał: "Dwie rzeczy natychmiast mnie zaskoczyły. Po pierwsze, fonnula dla
obszaru jest niezależna od wielkości danej krzywej C1I. Po drugie, [równanie dla powierzchni jest obszarem elipsy półosi p i q. ale w twierdzeniu nie ma elips! Twierdzenie to zostało opublikowane przez wielebnego Hamneta Holditcha w 1858 roku. Holditch był prezesem Caius College w Cambridge w połowie XIX wieku. Krzywa Holditcha C2 dla okręgu C1 o promieniu R to kolejne koło o promieniu r = √R2-pq
Georg Freidrich Bernhard Riemann (1826-1866)
Wiele badań matematycznych wskazuje, że "dowód hipotezy Riemanna" jest najważniejszym otwartym pytaniem w matematyce. Dowód obejmuje funkcję zeta, którą można przedstawić za pomocą skomplikowanej krzywej, która jest użyteczna w teorii liczb do badania właściwości liczb pierwszych. Zapisana jako ζ(x), funkcja został pierwotnie zdefiniowany jako nieskończona suma ζ(x) = 1 + (1/2)xx+ (1/4)x + … itd. Gdy x = 1, ta seria nie ma sumy skończonej. Dla wartości x większych niż 1, seria sumuje się do liczby skończonej. Jeśli x jest mniejsze niż 1, suma jest ponownie nieskończona. Pełna funkcja zeta, zbadana i omówiona w literaturze, jest bardziej skomplikowaną funkcją, która jest równoważna tej serii dla wartości x większych niż 1, ale ma skończone wartości dla dowolnej liczby rzeczywistej lub zespolonej, z wyjątkiem sytuacji, gdy część rzeczywista jest równa do 1. Wiemy, że funkcja jest równa zero, gdy x wynosi -2, - 4, -6, ... i że funkcja ma nieskończoną liczbę zerowych wartości dla zbioru liczb zespolonych. którego rzeczywista część wynosi od zera do jednego, ale nie wiemy dokładnie, jakie liczby zespolone występują w tych zerach. Matematyk Georg Bernhard Riemann wysunął przypuszczenie, że te zera występują dla liczb zespolonych, których rzeczywista część wynosi 1/2. Chociaż istnieją liczne dowody liczbowe przemawiające za tym przypuszczeniem, wciąż nie są one udowodnione. Dowód hipotezy Riemanna miałby głębokie konsekwencje dla teorii liczb pierwszych i dla naszego zrozumienia właściwości liczb zespolonych. O dziwo, fizycy mogli odkryć tajemniczy związek między fizyką kwantową a teorią liczb poprzez badania hipotezy Riemanna. Obecnie ponad 11 000 ochotników na całym świecie pracuje nad hipotezą Riemanna, używając rozproszonego pakietu oprogramowania komputerowego w Zetagrid.net do wyszukiwania zer funkcji zeta Riemanna. Ponad 1 miliard zer dla funkcji zeta jest obliczanych każdego dnia.
Eugenio Beltrami (1835-1899)
Pseudosfera to geometryczny obiekt, który przypomina dwa muzyczne rogi sklejone ze sobą na brzegach. "Ustniki" dwóch rogów znajdują się na końcach dwóch nieskończenie długich ogonów, jakby miały zostać wysadzone tylko przez wszechmocnych bogów. Ten szczególny kształt został szczegółowo omówiony w artykule z 1868 r. "Esej o interpretacji geometrii nieeuklidesowej" autorstwa włoskiego matematyka Eugenio Beltramiego, słynącego z pracy w geometrii i fizyce. Aby wytworzyć powierzchnię, krzywa zwana tractrix jest obracana wokół jej asymptoty. Podczas gdy zwykła kula ma właściwość o nazwie pozytywnej krzywizny wszędzie na swojej powierzchni, pseudosfera ma stałą krzywiznę ujemną, co oznacza, że można ją uważać za utrzymującą stałą wklęsłość na całej powierzchni (z wyjątkiem jej środkowego wierzchołka). Zatem kula jest zamkniętą powierzchnią ze skończonym obszarem, podczas gdy pseudosfera jest otwartą powierzchnią z nieliniowym obszarem. David Darling, brytyjski pisarz naukowy, pisze: "W rzeczywistości, chociaż płaszczyzna dwuwymiarowa i pseudosfera są nieliniowe, pseudosfera ma więcej miejsca! Jednym ze sposobów myślenia o tym jest to, że pseudosfera jest bardziej nieskończona niż płaszczyzna. " Ujemna krzywizna pseudosfery wymaga, aby kąty trójkąta narysowanego na jej powierzchni sumowały się poniżej 180o. Geometria pseudosfery nazywa się hiperboliczną, a niektórzy astronomowie w przeszłości sugerowali, że cały nasz wszechświat można opisać za pomocą geometrii hiperbolicznej o właściwościach pseudosfery. Pseudosfera ma znaczenie historyczne, ponieważ była jednym z pierwszych modeli przestrzeni nieeuklidesowej. Zainteresowania Beltrami sięgały daleko poza matematykę. Jego czterotomowe dzieło Opere Matematiche omawia optykę, termodynamikę, elastyczność, magnetyzm i elektryczność. Beltrami był członkiem Accademia dei Lmcei, pełniąc funkcję prezesa akademii naukowej w 1898 r. Został wybrany do Senatu Włoch na rok przed śmiercią.
Karl Theodor Wilhelm Weierstrass (1815-1897)
Na początku XIX wieku matematycy często myśleli o funkcji ciągłej f(x) jako posiadającej pochodną (unikalną linię styczną), którą można określić wzdłuż większości punktów na krzywej. W 1872 r. Niemiecki matematyk Karl Weierstrass oszołomił kolegów matematyków z Akademii Berlińskiej, udowadniając, że takie myślenie jest fałszywe. Jego funkcję, która była ciągła wszędzie, ale nigdzie nie rózniczkowalna (posiadająca pochodną), została zdefiniowana przez f(x) = Σakcos (bkπx), gdzie suma wynosi od k = 0 do ∞. Tutaj a jest liczbą rzeczywistą z zakresu 0 < a < 1, b jest nieparzystą liczbą całkowitą dodatnią, a ab > (1 + 3π/2). Symbol sumowania Σ wskazuje, że funkcja jest zbudowana z nieskończonej liczby funkcji trygonometrycznych, aby utworzyć gęsto zagnieżdżoną strukturę oscylacyjną. Oczywiście matematycy doskonale zdawali sobie sprawę z tego, że funkcje mogą nie być rozróżnialne w kilku kłopotliwych punktach, takich jak dno odwróconego kształtu klina określonego
przez f(x) = |x|, który nie ma pochodnej przy x = 0. Jednak po Weierstrassie, matematycy, którzy zademonstrowali krzywą nigdzie-różniczkowalną, byli w rozterce. Matematyk Charles Hermite napisał do Thomasa Stieltjesa w 1893 r. "J odwrócił się ze strachem i przerażeniem od żałosnej plagi ciągłych funkcji, które nie mają pochodnych. …" , W 1875 r. Paul du Bois-Reymond opublikował funkcję Weierstrass, czyniąc ją pierwszą opublikowaną funkcją tego rodzaju. Dwa lata wcześniej przekazał szkic artykułu Weierstrassowi do przeczytania (chociaż szkic zawierał inną funkcję f(x) = Σsin(anx)/bn, z (a/b) > 11 dla k = 0 do ∞, który został zmieniony przed opublikowaniem artykułu.) Podobnie jak inne kształty fraktalne, funkcja Weierstrass wyświetla rosnące szczegóły ze stopniowym powiększaniem. Inni matematycy, tacy jako czeski matematyk Bernard Bolzano i niemiecki matematyk Bernhard Riemann pracowali nad podobnymi (niepublikowanymi) konstrukcjami odpowiednio w 1830 i 1861 r. Innym przykładem ciągłej wszędzie, ale nigdzie różniczkowej krzywej jest fraktalna krzywa Kocha.
Louis Gros (ok. 1837 - 1907)
Baguenaudier to jedna z najstarszych znanych łamigłówek mechanicznych. W 1901 r. Angielski matematyk Henry E. Dudeney zauważył: "Z pewnością nie ma domu bez tej fascynującej, historycznej i pouczającej układanki". Baguenaudier ma na celu usunięcie wszystkich pierścieni ze sztywnej poziomej pętli. W pierwszym ruchu możliwe jest usunięcie jednego lub dwóch pierścieni z jednego końca drutu. Cała procedura jest skomplikowana, ponieważ pierścienie muszą zostać ponownie założone na pętlę z drutu, aby usunąć inne pierścienie, a procedura jest powtarzana wiele razy. Okazuje się, że minimalna wymagana liczba ruchów to (2n+1 - 2)/3, jeśli liczba pierścieni n jest parzysta, i (2n+1 - 1)/3, jeśli n jest nieparzysta. Martin Gardner pisze: "Dwadzieścia pięć pierścieni wymagają 22 369 621 kroków, zakładając, że wykwalifikowany operator może wykonać 50 kroków na minutę, mógłby to zrobić rozwiązać zagadkę ... za nieco ponad dwa lata". Według legendy, puzzle zostały wymyślone przez chińskiego generała Chu-ko Liang (181-234 n.e.), aby utrzymać żonę zajętą, gdy był na wojnie. W 1872 r. Louis Gros, francuski sędzia, wykazał wyraźny związek między tymi pierścieniami a liczbami binarnymi w swojej książeczce Theorie du Baguenodier (pisownia, którą wolał). Każdy pierścień może być reprezentowany przez cyfrę binarną: I dla włączenia i 0 dla wyłączenia. W szczególności Gros wykazał, że jeśli pierścienie były w zestawie znanych stanów, możliwe było obliczenie liczby binarnej, która wskazywałaby dokładnie, ile więcej kroków jest niezbędnych i wystarczających do rozwiązania zagadki. Prace Gros obejmowały jeden z pierwszych przykładów tego, co IS obecnie nazywa Szarym Kodem, w którym dwie kolejne liczby binarne różnią się tylko jedną cyfrą. W rzeczywistości informatyk Donald Knuth napisał, że Gros był "prawdziwym wynalazcą szarego kodu binarnego", który jest dziś szeroko stosowany w celu ułatwienia korekcji błędów w komunikacji cyfrowej.
Sofia Kowalewska(1850-1891)
Rosyjska matematyk Sofia Kowalewska wniosła cenny wkład w teorię równań różniczkowych i była pierwszą kobietą w historii, która otrzymała doktorat z matematyki. Podobnie jak większość innych geniuszy matematyki, Sofia zakochała się w matematyce w bardzo młodym wieku. W swojej autobiografii napisała: "Znaczenie tych pojęć, których naturalnie jeszcze nie rozumiałem, ale działały one na moją wyobraźnię, wzbudzając we mnie szacunek dla matematyki jako wzniosłej i tajemniczej nauki, która otwiera się na jej inicjację nowego świata cudów niedostępne dla zwykłych śmiertelników ". Kiedy Sofia miała 11 lata ściany jej sypialni pokryte były matematycznymi notatkami z wykładów Michaiła Ostrogradskiego na temat analizy różniczkowej i całkowej. W 1874 r. Kowalewska otrzymała doktorat summa cum laude z Uniwersytetu w Gottingen za pracę nad równaniami różniczkowymi cząstkowymi, całkami abelowymi i strukturą pierścieni Saturna. Jednak pomimo tego doktoratu i entuzjastycznych listów polecających od matematyka Karla Weierstrassa, Kovalevskaya przez lata nie była w stanie uzyskać stanowiska akademickiego, ponieważ była kobietą. Jednak w końcu zaczęła wykładać na uniwersytecie w Sztokholmie w Szwecji w 1884 r. W tym samym roku została powołana na pięcioletnią profesurę. W 1888 r. Paryska akademia nauk przyznała jej specjalną nagrodę za teoretyczne leczenie wirujących ciał stałych. Kowalevska zasługuje również na miejsce w historii matematyki, ponieważ była pierwszą rosyjską matematyczką o nadzwyczajnym znaczeniu, trzecią kobietą w historii, która została profesorem w Europie, poza Laurą Bassi (1711-1778) i Marią Agnesi (I71S-1799) - i pierwszą kobietą, która w dowolnym miejscu zajmuje katedrę uniwersytecką z matematyki. Osiągnęła te triumfy pomimo ostrego oporu. Na przykład jej ojciec zabronił jej studiowania matematyki, ale potajemnie uczyła się w nocy, gdy słynne rosyjskie kobiety nie mogły mieszkać bez rodzin bez pisemnej zgody ojca; w związku z tym została zmuszona do zawarcia małżeństwa, aby mogła wyjechać za granicę w celu dalszego kształcenia. Później w życiu napisała: "Nie można być matematykiem bez bycia poetą w duszy".
Noyes Palmer Chapman (1811-1889)
Chociaż Piętnastka nie jest poważnym kamieniem milowym, jak wiele innych naszych wpisów, wywołało takie poruszenie wśród publiczności, że warto o tym wspomnieć z przyczyn historycznych. Dziś możesz kupić wariant układanki z 15 kwadratami (kafelkami) i jednym wolnym miejscem w ramce lub pudełku 4 x 4. Na początku kwadraty kolejno zawierają liczby od 1 do 15, a następnie odstęp. W wersji układanki w Cyclopedii Sama Loyda z 1914 r. W konfiguracji początkowej odwrócono 14 i 15. Celem Loyda było "przesuwanie" kwadratów w górę, w dół, w prawo i w lewo, aby dojść do sekwencji od 1 do 15 (z 14 i 15 zamienionymi miejscami). W Cyclopedia Loyd twierdzi, że za rozwiązanie zaoferowano nagrodę w wysokości 1000 USD; Niestety, nie można rozwiązać zagadki z tej pozycji początkowej. Oryginalna wersja gry, opracowana w 1874 roku przez nowojorskiego postmistrza Noyesa Palmera Chapmana, odniosła natychmiastowy sukces w 1880 roku, podobnie jak kostka Rubika 100 lat później. Początkowo płytki były luźne, a gracz umieszczał je losowo, a następnie próbował rozwiązać. Zaczynając od losowych konfiguracji, zagadkę można rozwiązać tylko w 50 procentach przypadków! Od tego czasu matematycy dokładnie określili, które wstępne układy płytek mogą prowadzić do rozwiązań. Niemiecki matematyk W. Ahrens zauważył: "Piętnastka układała się w Stanach Zjednoczonych; szybko się rozprzestrzeniła, a dzięki niezliczonej liczbie oddanych graczy, których podbiła, stała się plagą". Co ciekawe, supergwiazda szachów Bobby Fischer był ekspertem w rozwiązywaniu łamigłówek w mniej niż 30 sekund, jeśli zaczęło się od dowolnej możliwej do rozwiązania konfiguracji.
Georg Cantor (1845-1918)
Niemiecki matematyk Georg Cantor założył nowozesną teorię zbiorów i wprowadził zadziwiającą koncepcję liczb pozaskończonych, których można użyć do oznaczenia względnych "rozmiarów" nieskończonej kolekcji obiektów. Najmniejsza liczba pozaskończona nazywa się aleph-zero, zapisana jako ℵ0, która liczy liczbę całkowitą. Jeśli liczba całkowita jest nieskończona (dla członków ℵ0), czy istnieją jeszcze wyższe poziomy nieskończoności? Okazuje się, że chociaż istnieje nieskończona liczba liczb całkowitych, liczb wymiernych (liczb, które można wyrazić jako ułamki) i liczb niewymiernych (takich jak pierwiastek kwadratowy z 2, których nie można wyrazić jako ułamek), nieskończona liczba niewymiernych jest w pewnym sensie większa niż nieskończona liczba racjonalnych lub liczb całkowitych. Podobnie, istnieje więcej liczb rzeczywistych (w tym liczb wymiernych i niewymiernych) niż liczb całkowitych. Szokujące koncepcje Cantora dotyczące nieskończoności spotkały się z powszechną krytyką - co prawdopodobnie przyczyniło się do napadów głębokiej depresji i licznych instytucjonalizacji Cantora, zanim zostały zaakceptowane jako podstawowa teoria. Cantor utożsamił także z Bogiem swoją koncepcję Absolutnej Nieskończoności, która wykraczała poza liczby nieskończone. Napisał: "Nie żywię wątpliwości co do prawd transfinitów. Które rozpoznałem z pomocą Boga i które w swojej różnorodności studiowałem przez ponad dwadzieścia lat". W 1884 r. Cantor napisał do szwedzkiego matematyka Gosty Mittag-Lefflera, wyjaśniając, że nie był twórcą swojego nowego dzieła, a jedynie reporterem. Bóg dostarczył inspiracji, pozostawiając Cantora odpowiedzialnym jedynie za organizację i styl jego dokumentów. Cantor powiedział, że wiedział, że transfinity są prawdziwe, ponieważ "Bóg tak mi powiedział", a to zmniejszyłoby moc Boga, gdyby Bóg stworzył tylko skończone liczby. Matematyk David Hilbert opisał pracę Cantora jako "najlepszy produkt geniuszu matematycznego i jednego o najwyższych osiągnięciach wyłącznie intelektualnej działalności człowieka ".
Franz Reuleaux (1829-1905)
Trójkąt Reuleaux (RT) jest jednym z przykładów szerokiej klasy odkryć geometrycznych, takich jak Wstęga Möbiusa, które nie znalazły wielu praktycznych zastosowań aż do stosunkowo późnego rozwoju intelektualnego ludzkości. Dopiero około 1875 r., kiedy wybitny inżynier mechanik niemiecki, Franz Reuleaux, omawiał słynny zakrzywiony trójkąt, zaczął znajdować wiele zastosowań. Chociaż Reuleaux nie był pierwszym, który narysował i rozważył kształt utworzony z przecięcia trzech kół na obrzeżach trójkąta równobocznego, był pierwszym, który zademonstrował jego właściwości stałej szerokości, i jako pierwszy zastosował trójkąt w wielu rzeczywistych światowe mechanizmy. Budowa trójkąta jest tak prosta, że nowi badacze zastanawiali się, dlaczego nikt przed Reuleaux nie wykorzystał jej zastosowania. Kształt jest bliskim krewnym koła ze względu na jego stałą szerokość, co oznacza, że odległość między dwoma przeciwnymi punktami jest zawsze taka sama. Różne patenty technologiczne koncentrują się na wiertłach, które wycinają kwadratowe otwory za pomocą RT. Na początku pojęcie wiertła, które tworzy prawie kwadratowe otwory, jest sprzeczne ze zdrowym rozsądkiem. Jak obrotowe wiertło może wyciąć coś oprócz okrągłego otworu? Ale takie wiertła istnieją .RT pojawia się również w patentach na inne wiertła, a także na nowe butelki, wałki, puszki po napojach, świece, obrotowe półki, skrzynie biegów, silniki obrotowe i szafki. Wielu matematyków badało trójkąt Reuleaux, więc wiemy dużo o jego właściwościach. Na przykład jego powierzchnia wynosi A = 1/2(π-√3)r2, a obszar wiercony wiertłem RT obejmuje 0,9877003907 ... powierzchni rzeczywistego kwadratu. Mała różnica występuje, ponieważ wiertło Reuleaux tworzy kwadrat z bardzo lekko zaokrąglonymi narożnikami.
Jean Baptiste Joseph Fourier (1768--1830), William Thomson, Baron Kelvin of Largs (1824-1907)
Na początku 1800 roku francuski matematyk Joseph Fourier stwierdził, że każdą funkcję różniczkowalną można przedstawić z dowolną dokładnością sumą funkcji sinus i cosinus, bez względu na to, jak skomplikowana jest ta funkcja. Na przykład funkcję okresową f(x) można przedstawić za pomocą sumy An⋅ sin (nx) + Bn⋅cos(nx) dla amplitud An i Bn. Analizator harmonicznych jest fizycznym urządzeniem do określania współczynników An i Bn. W 1876 r. Lord Kelvin, brytyjski fizyk matematyczny, jako pierwszy wynalazł analizator harmonicznych, służący do analizy śladów krzywych związanych z obserwacjami pływów oceanicznych. Papier z krzywą zainteresowania jest owinięty wokół głównego cylindra. podążać za krzywą, a następnie określa się pozycje różnych podskładników, aby uzyskać pożądane współczynniki. Kelvin pisze, że "maszyna kinematyczna" przewiduje nie tylko "czasy i wysokości wysokiej wody, ale głębokości wody w dowolnym momencie, pokazując je
ciągłą krzywą z …wyprzedzeniem". Ponieważ przypływy zależą od położenia słońca, księżyca, obrotu ziemi, kształtu linii brzegowej i profilu dna morskiego, mogą być dość złożone. W 1894 r. , niemiecki matematyk Olaus Henrici (1840-1918 ) zaprojektował analizator harmonicznych do ustalania składowych harmonicznych złożonych fal dźwiękowych, takich jak te pochodzące z instrumentów muzycznych. W urządzeniu zastosowano kilka kół pasowych i szklanych kul połączonych z tarczami pomiarowymi, które dały fazę i amplitudy 10 składowych harmonicznych Fouriera. W 1909 r. Niemiecki inżynier Otto Mader wynalazł analizator harmonicznych, który wykorzystywał koła zębate i wskaźnik do śledzenia krzywej; różne biegi odpowiadały lewej harmonicznej. Analizator harmonicznych Montgomery′ego z 1938 r. stosował optyczne i fotoelektryczne środki do określania zawartości krzywej harmonicznej. H. C. Montgomery z Bell Laboratories napisał, że urządzenie "jest specjalnie przystosowane do analizy mowy i muzyki, ponieważ pochodzi
bezpośrednio od konwencjonalnego typu ścieżki dźwiękowej na filmie".
James Ritty (1836--1918)
Trudno sobie wyobrazić, jak sklepy detaliczne mogłyby działać skutecznie, zanim istniały kasy fiskalne. Przez dziesięciolecia kasy stały się coraz bardziej wyrafinowane i działały również jako środki zapobiegające kradzieży. Nie jest przesadą stwierdzenie, że stały się jedną z głównych mechanizujących transformacji epoki przemysłowej. Pierwsza kasa została wynaleziona w 1879 roku przez Jamesa Ritty′ego. Ritty otworzył swój pierwszy salon w Dayton w stanie Ohio w 1871 roku, określając siebie mianem "dilera czystych whisky, szlachetnych win i cygar". Największym wyzwaniem dla Ritty były jego pracownicy, którzy czasami potajemnie chowali pieniądze otrzymane od klientów. Podczas rejsu statkiem parowym Ritty studiował mechanizm, który liczył liczbę obrotów śmigła statku, i zaczął wyobrażać sobie podobne mechanizmy, które można wykorzystać do rejestrowania transakcji gotówkowych. Wczesne maszyny Ritty miały dwa rzędy klawiszy, z których każdy odpowiadał nominałowi pieniędzy od pięciu centów do jednego dolara. Naciśnięcie klawiszy obróciło wał, który przesunął wewnętrzny licznik. Opatentował swój projekt w 1879 r. Jako "Niesprawiedliwy kasjer Rilly". Rilly wkrótce sprzedał swoją kasę fiskalną sprzedawcy o imieniu Jacob H. Eckert, a w 1884 r. Eckert sprzedał firmę Johnowi H. Pattersonowi, który przemianował firmę na National Cash Register Company. Z małego ziarna Ritty wyrosła nowoczesna kasa fiskalna. Patterson dodał rolki papieru do rejestrowania transakcji za pomocą dziurkaczy. Kiedy transakcja została zakończona, na kasie zabrzmiał dzwonek, a kwota pieniężna była reprezentowana na dużej tarczy. W 1906 roku wynalazca Charles F. Kettering zaprojektował kasę z silnikiem elektrycznym. W 1974 r. National Cash Register Company przekształciło się w NCR Corp. Dziś funkcjonalność kasy fiskalnej wykracza poza najśmielsze marzenie Ritty, ponieważ to maszyny ze znacznikami czasu, pobieranie cen z baz danych i obliczanie odpowiednich kwot podatku, różnych stawek dla preferowanych klientów oraz potrąceń za pozycje sprzedaży.
John Venn (1834-1923)
W 1880 r. John Venn, brytyjski filozof i duchowny w Kościele anglikańskim, opracował schemat wizualizacji elementów, zbiorów i relacji logicznych. Diagram Venna zwykle zawiera okrągłe obszary reprezentujące grupy przedmiotów o wspólnych właściwościach.
Na przykład we wszechświecie wszystkich prawdziwych i legendarnych stworzeń (prostokąt na pierwszej ilustracji) obszar H reprezentuje ludzi, obszar W - skrzydlate stworzenia, a obszar A - anioły. Rzut oka na diagram pokazuje, że (I) Wszystkie anioły są skrzydlatymi stworzeniami (obszar A leży całkowicie w obszarze W); (2) Żaden człowiek nie jest skrzydlatym stworzeniem (regiony Hand Ware nie przecinają się); oraz (3) Żaden człowiek nie jest aniołem (obszary H i A nie przecinają się). Jest to przedstawienie podstawowej zasady logiki - mianowicie, że ze stwierdzeń "wszystko A jest W" i "nie ma H jest W", z tego wynika, że "nie H jest A" Wniosek jest oczywisty, gdy spojrzymy na koła w diagram. Zastosowania tego rodzaju diagramów w logice były używane przed Vennem - na przykład przez matematyków Gottfrieda Leibniza i Leonharda Eulera - ale Venn był pierwszym, który kompleksowo je przestudiował, zgrupował i uogólnił ich użycie. W rzeczywistości Venn walczył z uogólniając symetryczne diagramy do wizualizacji większej liczby zestawów z przecinającymi się obszarami, ale za pomocą elips osiągnął tylko 4 zestawy. Minął wiek, więc Branko Grunbaum, matematyk z University of Washington, pokazał, że obrotowo symetryczne diagramy Venna można wykonać z 5 przystających elipsy. Druga ilustracja pokazuje jeden z wielu różnych schematów symetrycznych dla 5 zestawów. Matematycy stopniowo zdawali sobie sprawę, że schematy symetryczne obrotowo można rysować tylko z liczbami pierwszymi płatków. Jednak symetryczne diagramy etyczne z 7 płatkami były tak trudne do znalezienia, że matematycy początkowo wątpili w ich istnienie. W 2001 roku matematyk Peter Hamburger i artysta Edit Hepp skonstruowali przykład dla II płatków, pokazany na przeciwnej stronie.
Simon Newcomb (1835-1909), Frank Benford (1883-1948)
Prawo Benforda, zwane również zjawiskiem prawem pierwszej liczby lub wiodącej liczby, stwierdza, że na różnych listach liczb cyfra I ma tendencję do występowania w skrajnej lewej pozycji z prawdopodobieństwem około 30 procent, znacznie większym niż oczekiwane 11.1. Procentowy wynik, który wystąpiłby, gdyby każda cyfra wystąpiła z prawdopodobieństwem mniejszym niż 9. Prawo Benforda może być przestrzegane, na przykład, w tabelach zawierających populacje, wskaźniki śmiertelności, ceny akcji, statystyki baseballu oraz obszar rzek i jezior. Wyjaśnienia tego zjawiska są bardzo nowe. Prawo Benforda nosi imię dr Franka Benforda, fizyka z General Electric , który opublikowała swoją pracę w 1938 r., Chociaż zostało odkryte wcześniej przez matematyka i astronoma Simona Newcomba w 1881 r. strony logarytmów z liczbami rozpoczynającymi się od cyfry mówi się, że są brudniejsze i bardziej zużyte niż inne strony, ponieważ liczba 1 występuje jako pierwsza cyfra około 30 procent częściej niż jakikolwiek inny. W wielu rodzajach danych Benford ustalił, że prawdopodobieństwo dowolnej liczby n od 1 do 9 jako pierwszej cyfry wynosi log10(1 + 1/n). Nawet ciąg Fibonacciego - 1, 1, 2, 3, 5, 8, 13 … - jest zgodna z prawem Benforda. Liczby Fibonacciego znacznie częściej zaczynają się od "1" niż jakakolwiek inna cyfra. Wydaje się, że prawo Benforda ma zastosowanie do wszelkich danych zgodnych z "prawem władzy". Na przykład duże jeziora są rzadkie, jeziora średniej wielkości są bardziej powszechne, a małe jeziora są jeszcze bardziej powszechne. Podobnie, 11 liczb Fibonacciego występuje w zakresie 1-100, ale tylko jeden w kolejnych trzech zakresach 100 (101-200,201-300,301-400). Prawo Benforda było często wykorzystywane do wykrywania oszustw. Na przykład użytkownicy rachunków mogą czasami wykorzystywać prawo do wykrywania fałszywych deklaracji podatkowych, w których występowanie cyfr nie jest zgodne z tym, czego zgodnie z prawem Benforda można się naturalnie spodziewać.
Felix Klein (1849-1925)
Butelka Klein, po raz pierwszy opisana w 1882 r. przez niemieckiego matematyka Felixa Kleina, jest przedmiotem, w którym elastyczna szyjka butelki opada z powrotem w butelkę, tworząc kształt bez wnętrza i na zewnątrz. Ta butelka jest powiązana z paskiem Mobiusa i teoretycznie może być utworzona przez sklejenie dwóch pasków Mobiusa razem wzdłuż ich krawędzi. Jedna droga do zbudowanie niedoskonałego modelu fizycznego butelki Kleina w naszym wszechświecie 3-D polega na tym, aby spotkała się na małej, okrągłej krzywej. Potrzebne są cztery wymiary, aby stworzyć prawdziwą butelkę Kleina bez samo-skrzyżowań. Wyobraź sobie swoją frustrację, jeśli próbujesz pomalować tylko zewnętrzną stronę butelki Kleina. Zaczynasz malować na czymś, co wydaje się być bulwiastą "zewnętrzną" powierzchnią i schodzisz po wąskiej szyi. Obiekt 4-0 nie przecina się, co pozwala kontynuować podążanie za szyją, która jest teraz "wewnątrz" butelki. Gdy szyja otwiera się, aby ponownie dołączyć do bulwiastej powierzchni, okazuje się, że malujesz teraz w butelce. Gdyby nasz wszechświat kształtował się jak butelka Kleina, moglibyśmy znaleźć ścieżki, które sprawiłyby, że nasze ciała odwróciłyby się po powrocie po podróży, tak że na przykład nasze serca byłyby po prawej stronie naszego ciała. Wraz z Centrum Kingbridge w Toronto i Killdee Scientific Glass astronom Cliff Stoll stworzył największy na świecie model szklanej butelki Klein. Butelka Kingin Klein ma około 43 cali (1,1 metra) wysokości i 20 cali (50 centymetrów) średnicy. i jest wykonany z 33 funtów (15 kilogramów) przezroczystego szkła Pyrex. Ze względu na szczególne właściwości butelki Kleina, matematycy i entuzjaści puzzli studiują szachy i labirynty rozgrywane na powierzchniach butelek Klein. Gdy narysowano mapę na butelce Kleina, potrzeba sześciu różnych kolorów, aby zapewnić, że żadne obszary graniczne nie będą miały tego samego koloru.
Francois Edouard Anatole Lucas (1842-1891)
Wieża z Hanoi zaintrygowała świat, odkąd została wynaleziona przez francuskiego matematyka Edouarda Lucasa w 1883 roku i sprzedana jako zabawka. Ta matematyczna łamigłówka składa się z kilku dysków o różnych rozmiarach, które wsuwają się na jeden z trzech kołków. Dyski są początkowo układane w stos na jednym kołku w kolejności wielkości, z najmniejszym dyskiem u góry. Podczas gry można przenosić jeden dysk na inny kołek, usuwając górny dysk z dowolnego stosu i umieszczając go na szczycie dowolnego innego stosu. Dysku nie można umieścić na mniejszym dysku. Celem jest przeniesienie całego stosu początkowego (często z ośmioma dyskami) na inny kołek. Minimalna liczba ruchów okazuje się wynosić 2n - 1 I, gdzie n to liczba dysków. Oryginalna gra została zainspirowana legendarną Indian Tower of Brahma, która zatrudniała 64 złote dyski. Kapłani Brahmy ciągle poruszali te dyski, przy użyciu tych samych zasad, co w Wieży Hanoi. Po zakończeniu ostatniego ruchu układanki świat się skończy. Pamiętaj, że jeśli kapłani będą mogli przenosić dyski w tempie 1 na sekundę, wówczas 264 - lub 18 446,744,073,709,551,615 ruchów wymagałoby około 585 miliardów lat - wiele razy więcej niż obecny szacowany wiek naszego wszechświata. Istnieją proste algorytmy dla rozwiązań obejmujących trzy pegi, a gra jest często używana w klasach programowania komputerowego do nauczania algorytmów rekurencyjnych. Jednak optymalne rozwiązanie dla problem Wieży Hanoi z czterema lub więcej kołkami jest nadal nieznany. Matematycy uważają tę zagadkę za intrygującą ze względu na jej związki z innymi obszarami matematyki, w tym Gray Codes i znajdowanie ścieżek hamiltonowskich na n-hipersześcianie.
Edwin Abbott Abbott (1838-1926)
Ponad sto lat temu Edwin Abbott Abbott - duchowny i dyrektor szkoły w wiktoriańskiej Anglii - napisał wpływową książkę opisującą interakcje między stworzeniami z dostępem do różnych wymiarów przestrzennych. Książka jest nadal popularna wśród studentów matematyki i uważana za przydatną lekturę dla każdego, kto studiuje związki między takimi wymiarami. Abbott zachęcił czytelników, aby otworzyli swoje umysły na nowe sposoby postrzegania. Flatland opisał rasę dwuwymiarowych stworzeń, żyjących w płaskiej płaszczyźnie, zupełnie nieświadomy istnienia wokół siebie wyższego wymiaru. Gdybyśmy byli w stanie spojrzeć w dół na dwuwymiarowy świat, bylibyśmy w stanie zobaczyć wnętrze każdej struktury naraz. Istota z dostępem do czwartego wymiaru przestrzennego mogła zobaczyć wnętrze naszego ciała i usunąć guz bez penetracji skóry. Flatlanderzy mogą nie zdawać sobie sprawy z tego, że stanąłeś kilka cali nad ich planarnym światem, rejestrując wszystkie wydarzenia z ich życia. Jeśli chcesz usunąć Flatlandera z więzienia, możesz go podnieść "do góry" i złożyć go w innym miejscu w Flatland. Ten akt wydawałby się cudowny dla Flatlandera, który nawet nie miałby tego słowa w swoim słownictwie. Dzisiaj komputerowe projekcje graficzne obiektów 4-D przybliżają nas o krok do zjawisk wielowymiarowych, ale nawet najbardziej błyskotliwi matematycy często nie są w stanie uchwycić czwartego wymiaru, podobnie jak kwadratowy bohater Flatland miał problemy ze zrozumieniem trzeciego wymiaru. W jednej z najbardziej emocjonalnych scen Flatlandu dwuwymiarowy bohater staje w obliczu zmieniających się kształtów trójwymiarowej istoty, która przechodzi przez Flatland. Kwadrat może zobaczyć tylko przekroje stworzenia. Abbott uważał, że badanie czwartego wymiaru przestrzennego jest ważne w rozwijaniu naszej wyobraźni, zwiększaniu szacunku dla wszechświata i zwiększaniu naszej pokory, być może pierwsze kroki w jakiejkolwiek próbie lepszego zrozumienia natury rzeczywistości lub dostrzeżenia boskości
Charles Howard Hinton (1853-1907)
Nie znam żadnego przedmiotu w matematyce, który zaintrygowałby zarówno dzieci, jak i dorosłych, jak idea czwartego wymiaru, kierunku przestrzennego odmiennego od wszystkich kierunków naszej codziennej trójwymiarowej przestrzeni. Teologowie spekulują, że życie pozagrobowe, niebo, piekło, anioły i nasze dusze mogą przebywać w czwartym wymiarze. Matematycy i fizycy często używają czwartego wymiaru w swoich obliczeniach. Jest to część ważnych teorii opisujących samą tkankę naszego wszechświata. Tesseract jest czterowymiarowym analogiem zwykłej kostki. Termin hipersześcian jest używany bardziej ogólnie w odniesieniu do analogów kostki w innych wymiarach. Tak jak sześcian może zostać zwizualizowany poprzez przeciągnięcie kwadratu do trzeciego wymiaru i obserwowanie kształtu, który kwadrat śledzi w przestrzeni, tesseract jest wytwarzany przez ślad sześcianu przesuwającego się do czwartego wymiaru. Chociaż trudno jest wyobrazić sobie przesunięcie sześcianu na odległość w kierunku prostopadłym do wszystkich trzech jego osi, grafika komputerowa często pomaga matematykom rozwinąć lepszą intuicję dla obiektów wielowymiarowych. Zauważ, że sześcian jest ograniczony kwadratowymi fuksami, a tesseract sześciennymi fuksami. Możemy zapisać liczbę narożników, krawędzi, otworów i brył dla tego rodzaju obiektów o wyższych wymiarach. Słowo tesseract zostało wymyślone i użyte po raz pierwszy w 1888 r. Przez brytyjskiego matematyka Charlesa Howarda Hintona w jego książce Nowa era myśli. Hinton, bigamista, był również wściekły na swój zestaw kolorowych kostek, które, jak twierdził, mogłyby być wykorzystane do pomocy ludziom w wizualizacji czwartego wymiaru. Kiedy używano ich na seansach, uważano, że kostki Hinton pomagają ludziom dostrzec duchy zmarłych członków rodziny.
Giuseppe Peano (1858-1932)
Dzieci w wieku szkolnym znają proste reguły arytmetyczne liczenia, dodawania i mnożenia, ale skąd się biorą te najprostsze reguły i skąd wiemy, że są poprawne? Włoski matematyk Giuseppe Peano znał pięć aksjomatów lub założeń Euklidesa, które położyły podwaliny pod geometrię, a Peano był zainteresowany stworzeniem tego samego rodzaju podstaw dla arytmetyki i teorii liczb. Pięć aksjomatów Peano obejmuje nieujemne liczby całkowite i można je określić jako: 1) 0 jest liczbą; 2) Następcą dowolnej liczby jest liczba; 3) Jeśli n i m są liczbami i jeśli ich następcy są równi, to n i m są równe; 4) 0 nie jest następcą żadnej liczby; oraz 5) Jeśli S jest zbiorem liczb zawierających 0 i jeśli następca dowolnej liczby w S jest również w S, wówczas S zawiera wszystkie liczby. Piąty aksjomat Peano pozwala matematykom ustalić, czy właściwość jest prawdziwa dla wszystkich liczb nieujemnych. Aby to osiągnąć, najpierw musimy pokazać, że 0 ma właściwość. Następnie musimy pokazać, że dla dowolnej liczby i, jeśli i ma właściwość, oznacza to, że i + 1 również ma tę właściwość. Metafora pomaga. Wyobraź sobie nieskończoną linię zapałek, prawie wzruszające. Jeśli chcemy, aby wszystkie się paliły, pierwsza zapałka musi się zapalić, a każda zapałka w linii musi być wystarczająco blisko, aby mogła się zapalić. Jeśli jedna zapałka na linii ma zbyt dużą separację, ogień ustaje. Za pomocą aksjomatów Peano możemy zbudować system arytmetyczny, który obejmuje nieskończony zestaw liczb. Aksjomaty stanowią podstawę naszego systemu liczbowego i pomagają matematykom konstruować inne systemy liczbowe stosowane w nowoczesnej matematyce. Peano po raz pierwszy przedstawił swoje aksjomaty w swojej 1889 Arithmetices principia, nova methodo exposita (Zasady arytmetyki, przedstawione nową metodą).
Giuseppe Peano (1858-1932)
W 1890 roku włoski matematyk Giuseppe Peano przedstawił jeden z pierwszych przykładów krzywej wypełniającej przestrzeń. David Darling, brytyjski pisarz naukowy, nazywa to odkrycie "trzęsieniem ziemi związanym z tradycyjną strukturą matematyki". Omawiając tę nową klasę krzywych, rosyjski matematyk Naum Wilenkin napisał, że "wszystko było w ruinie, że wszystkie podstawowe pojęcia matematyczne straciły na znaczeniu". Termin Krzywa Peano jest często używany jako synonim krzywej wypełniającej spację, oraz ,że takie krzywe mogą często być tworzone przez iteracyjny proces, który ostatecznie tworzy zygzakowatą linię, która pokrywa całą przestrzeń, w której się znajduje. Martin Gardner pisze: "Krzywe Peano były głębokim szokiem dla matematyków. Ich ścieżki wydają się być jednowymiarowe, ale na granicy zajmują dwuwymiarowy obszar. Czy powinny być nazywane krzywymi? Co gorsza, krzywe Peano można narysować tak łatwo aby wypełnić kostki i hipersześciany ... "Krzywe Peano są ciągłe, ale jak granica płatka śniegu Kocha lub funkcji Weierstrassa, żaden punkt na krzywej nie ma charakterystycznej stycznej. Krzywe wypełniające przestrzeń mają wymiar Hausdorffa wynoszący 2. Krzywe wypełniające przestrzeń miały praktyczne zastosowania i sugerowały efektywne trasy do odwiedzenia podczas odwiedzania wielu miast. Na przykład John J. Bartholdi III, profesor w Szkole Inżynierii Przemysłowej i Systemowej w Georgia Institute of Technology, wykorzystał krzywe Peano do zbudowania systemu routingu dla organizacji, która dostarcza biednym setki posiłków i kieruje krew dostawa przez Amerykański Czerwony Krzyż do szpitali. Ponieważ lokalizatory dostarczania są zwykle skupione wokół obszarów miejskich, użycie wypełniających przestrzeń krzywych Bartholdigo daje bardzo dobre sugestie trasowania, ponieważ krzywe odwiedzają wszystkie lokalizacje w regionie mapy przed przejściem do innego regionu. Naukowcy eksperymentowali również z krzywymi wypełniania przestrzeni dla celowania broni, ponieważ można zastosować technikę matematyczną, dzięki czemu działa ona bardzo skutecznie na komputerze wysyłanym na orbitę wokół Ziemi.
Evgraf Stepanovich Fedorov (1853-1919), Arthur Moritz Schonflies (1853-1928), William Barlow (1845-1934)
Wyrażenie "grupy tapet" odnosi się do sposobów, w jakie płaszczyzna może być kafelkowana, dzięki czemu powstały wzór powtarza się w nieskończoność w dwóch wymiarach. Istnieje siedemnaście wzorów tapet, z których każdy jest identyfikowany przez symetrie, takie jak te obejmujące tłumaczenia (na przykład przesunięcie lub przesunięcie) i rotację. Wybitny rosyjski krystalograf E. S. Fiodorow odkrył i sklasyfikował te wzory w 1891 r. Wzory te były również badane niezależnie przez niemieckiego matematyka A. M. Schonfliesa i angielskiego krystalografa Williama Barlowa. Trzynaście z tych wzorów (formalnie znanych jako izometria) obejmuje pewną symetrię obrotową, podczas gdy cztery nie. Pięć pokazuje sześciokątne symetrie. Dwanaście pokazuje prostokąt symetrie. Maron Gardner pisze: "Istnieje siedemnaście różnych grup symetrii, które wykazują wszystkie zasadniczo różne sposoby powtarzania wzorów w nieskończoność w dwóch wymiarach. Elementy tych grup są po prostu operacjami wykonywanymi na jednym podstawowym wzorze: ślizganie się wzdłuż płaszczyzny. Obracanie lub odwrócenie lustra. Siedemnaście grup symetrii ma ogromne znaczenie w badaniu struktury kryształu". Geometria H. S. M. Coxeter zauważył, że sztuka wypełniania samolotu powtarzalnym wzorem osiągnęła swój szczyt w XIII-wiecznej Hiszpanii, gdzie Maurowie Maurowie wykorzystali wszystkie 17 grup w swoich pięknych dekoracjach pałacu i fortecy Alhambra. Ponieważ niektóre tradycje islamskie zniechęcały do wykorzystywania wizerunków ludzi w dziełach sztuki, symetryczne wzory tapet stały się szczególnie atrakcyjne jako dekoracje. Pałac Alhambra w Granadzie zawiera skomplikowane arabeskowe wzory, które zdobią płytki , tynki i rzeźby w drewnie. Wizyta holenderskiego artysty M. C. Eschera (1898--1972) w pałacu Alhambra wpłynęła na jego własną sztukę, która często jest pełna symetrii. Escher powiedział kiedyś, że jego wycieczki do Alhambry były "najbogatszym źródłem inspiracji, jakie kiedykolwiek wykorzystałem". Escher próbował "ulepszyć" dzieła Maurów, wykorzystując geometryczne siatki jako podstawę swoich szkiców, które następnie nałożył na projekty zwierząt