układ równań : Zestawienie równań, które mają być wszystkie spełnione przez te same wartości niewiadome. Układ dwu równań o dwu niewiadomych można zapisać ogólnie w postaci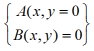

gdzie A(x,y) i B(x,y) są to wyrażenia zawierające niewiadome x i y. Rozwiązaniem powyższego układu równań nazywamy każdą parę liczb (x,y), któa spełnia każde z nich. Rozwiązać układ równań oznacza to znaleźć wszystkie jego rozwiązania. Jeżeli A(x,y) i B(x,y) są wielomianami, to układ równań nazywamy algebraicznym. Układ równań może mieć skończoną liczbę równań [układ oznaczony],może mieć nieskończenie wiele rozwiązań [układ nieoznaczony], może nie mieć rozwiązań [układ sprzeczny]. W przypadku szczególnym układu dwu równań stopnia pierwszego o dwu niewiadomych: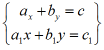

układ jest oznaczony, gdy ab₁ - ba₁ ≠ 0, przy czym mamy wówczas
x= cb₁-bc₁ / ab₁-ba₁, y = ac₁-ca₁ / ab₁-ba₁, nieoznaczony gdy zachodzi proporcja a : a₁ = b : b₁ = c : c₁ (jeśli któryś ze współczynników jest zerem, to proporcje uważamy za spełnioną, jeśli towarzyszący mu w niej drugi współczynnik jest także zerem),sprzeczny zaś , gdy ab₁-ba₁ = 0; lecz proporcja powyższa nie jest spełniona. Powyższe trzy przypadki można zilustrować graficznie , wykreślając proste, jakie przedstawiają poszczególne równania (a² + b² > 0,a₁²+b₁² > 0). w podobny sposób rozwiązuje się i analizuje układy równań pierwszego stopnia o większej liczbie niewiadomych. Do układu równań , które nie są algebraiczne należą w szczególności układy równań niewymiernych, układy równań trygonometrycznych, układy równań logarytmicznych, wykładniczych i in.

układ równań algebraicznych : układ równań

układ równań nieoznaczony : układ równań

układ równań oznaczony : układ równań

układ równań sprzeczny : układ równań

układ współrzędnych : Układ linii zwanych osiami współrzędnych, względem których określamy położenie punktów. Liczby charakteryzujące położenie punktu względem tych linii nazywamy współrzędnymi punktu. Najwcześniej posługiwano się współrzędnymi geograficznymi i astronomicznymi przy określaniu położenia punktów na niebie i luki ziemskiej (szerokość i długość geograficzna). Od XVII wieku, dzięki francuskiemu matematykowi Kartezjuszowi (Descartes), zaczęto powszechnie używać współrzędnych prostokątnych zwanych kartezjańskimi. Układ współrzędnych prostokątnych na płaszczyźnie jest to układ dwóch prostych prostopadłych zwanych osiami układu współrzędnych; oś x nazywamy osią odciętych, a oś y - osią rzędnych. Kierunek wzrastania wartości liczbowych odpowiadających punktom osi zaznaczamy strzałką .Punkt przecięcia osi nazywamy początkiem układu współrzędnych. Przyjęto umowę ,że by za dodatnio zorientowany (lewoskrętny) uważać układ współrzędnych , w którym kąt od dodatniej części osi x do dodatniej części osi y jest mierzony w przeciwnym kierunku do ruchu wskazówek zegara. Odpowiednio określa się układ zorientowany ujemnie (prawoskrętny).Współrzędne biegunowe jest to para liczb r i φ przyporządkowana każdemu punktowi, gdzie r jest długością odcinka (promieniem wodzącym) łączącego ten punkt ze pewnym ustalonym punktem zwanym biegunem, a φ jest kątem między promieniem wodzącym a pewnym ustalonym promieniem o wierzchołku w biegunie, zwanym osią biegunową; kąt &phi nazywamy amplitudą (albo fazą) punktu M .Jeżeli biegun jest początkiem układu współrzędnych prostokątnych a oś biegunowa dodatnią półosią x, to zachodzą zależności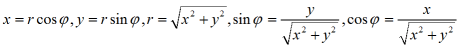
.
Zależności te są wzajemnie jednoznaczne przy 0 < r < ∞, 0 ≤ φ < 2π, x² + y² ≠ 0 , natomiast w biegunie r = 0 a kąt φ jest nieokreślony. Przy ciągłym ruchu puntu dookoła bieguna uwzględniamy liczbę obrotów φ = φ₀ +2kπ gdzie 0 ≤ φ₀ < 2π.
Układ współrzędny ukośnokątnych tworzą dwie proste przecinające się pod pewnym kątem ζ ≠ 90⁰. Jeśli z punku M poprowadzimy proste równoległe do osi , to otrzymamy współrzędne ukośnokątne punktu M: x=)A;y=OB. Układ współrzędnych ukośnokątnych używany jest m.in. w krystalografii. Układ współrzędnych prostokątnych i ukośnokątnych nazywamy układami współrzędnymi prostoliniowymi. Istnieją również układy współrzędnych krzywoliniowych barycentrycznych i in. Układ współpodrzędnych prostokątnych w przestrzeni stanowią trzy proste wzajemnie prostopadłe, zwane osiami układu współrzędnych, przecinające się w jednym punkcie zwanym początkiem układu współrzędnych. Strzałką zaznaczamy kierunek wzrastania wartości liczbowych odpowiadających punktom osi. Gdy stojąc w pionie osi (z głową zwróconą w kierunku dodatnim osi) i patrząc na pierwszą ćwiartkę płaszczyzny xy widzimy oś x po lewej stronie, to układ współrzędnych jest lewoskrętny; gdy obserwator znajdujący się w poprzednim położeniu widzi os x po prawej stronie, układ współrzędnych jest prawoskrętny. Jeżeli wprowadzimy jednakowe odcinki jednostkowe na osiach, to otrzymamy prostokątny układ współrzędnych kartezjańskich. Położenie każdego punktu określone jest trójką liczb (x,y,z) zwanych współrzędnymi punktu.
Współrzędne walcowe jest to układ trzech liczb r,φ, z^, gdzie z^ jest odległością względną (z uwzględnieniem znaku) punktu M od ustalonej płaszczyzny, a r i φ - współrzędnymi biegunowymi w tej płaszczyźnie rzutu punktu M na tą płaszczyznę (ON=r).
Współrzędne sferyczne jest to trójka wielkości R,φ, ζ określająca położenie punktu w przestrzeni. Odcinek OM=R nazywamy promieniem wodzącym punktu, φ jest to kąt pomiędzy rzutem odcinka OM na płaszczyznę xy i dodatnią półosią x (długość geograficzna), ζ - kat pomiędzy promieniem wodzącym OM i płaszczyzną xy (szerokość geograficzna), przy czym 0 < R < ∞, 0 ≤ φ < 2π -(π/2) ≤ ζ ≤ π/2. Współrzędne sferyczne związane są z prostokątnymi następującymi wzorami : x = R cos φ cos ζ , y = R sin φ cos ζ, z = R sin ζ . Kat φ nazywamy również azymutem, a ζ - kątem podniesienia. Jeżeli ζ jest kątem pomiędzy promieniem wodzącym OM i osią z to zachodzą zależności: x =R cos φ sin ζ, y = R sin φ sin ζ, z = R cos ζ (0 ≤ ζ ≤ π). Używane są również w przestrzeni układów współrzędnych ukośnokątnych i krzywoliniowych

Ulam Stanisław Marcin (1909-1984) : Matematyk amerykański pochodzenia polskiego, autor prac z teorii mnogości, teorii funkcji rzeczywistych, teroi grup , rachunku prawdopodobieństwa i fizyki matematycznej.

ułamek : Pojęcie arytmetyki, które pojawiło się prawdopodobnie równocześnie z pojęciem liczb naturalnych. Najwcześniejsze historycznie pojęcie połowy (na co wskazuje m.in. istnienie w różnych językach specjalnej jej nazwy),a następnie trzeciej części i czwartej części. Pojęcie ułamka jest związane z dzieleniem. Już w babilońskim systemie miar wprowadzono części pewnych jednostek (1 miona = 1/60 talenta i 1 szekel = 1/60 miny były miarami wag), w starożytnym Rzymie dzielono 1 as na 12 uncji. Ułamek postaci l/m (l - licznik, m - mianownik są liczbami naturalnymi, wany dziś ułamkiem zwykłym, rozpowszechnił się dzięki Grekom i Hindusom .Zasady działań arytmetycznych nad ułamkami zwykłymi powstały w Indiach (VIII w. n.e.),skąd przez kraje arabskie dotarły do Europy w XIII w., głównie dzięki Fibonacciemu. Jednocześnie z ułamkami zwykłymi były używane do XVII w. ułamki sześćdziesiętne (szczególnie w astronomii), które zostały następnie zamienione ułamkami dziesiętnymi wprowadzonymi przez Holendra, S.Stevina.

ułamek ciągły : ułamek łańcuchowy

ułamek dziesiętny : Ułamek o mianowniku będącym potęgą 10, wprowadzony dla ułatwienia działań arytmetycznych nad ułamkami zwykłymi, które to działania w przypadku dużych mianowników są bardzo pracochłonne .Zapis ułamka dziesiętnego nie wymaga kreski ułamkowej,zaznaczamy jedynie na prawo od przecinka licznik sumy ułamków zwykłych o mianownikach będących kolejnymi potęgami 10, która przedstawia zapisywany ułamek , np. 0,5128 = 5/10+1/10²+2/10³+8/10⁴. Jeżeli ułamek nie jest właściwy, to cyfry na lewo do przecinka oznaczają liczbę jedności, dziesiątek , setek itd, np. 281,52 = 2*100+8*10+1*1+5/10+2/10². Ułamków dziesiętnych używa się powszechnie w rachunkach praktycznych ze względu na prostotę algorytmów dotyczących działań nad nimi.

ułamek dziesiętny nieskończony : Przedstawienie liczby rzeczywistej za pomocą szeregu liczbowego x = a₀ + a₁/10 + a₂ / a² + a₃ / 10³+... , gdzie a₀ jest pewną liczbą całkowitą ,zaś a_n (n=1,2..) są to liczby całkowite spełniające warunek 0 ≤ a_n ≤ 9 . Symbol a₀ a₁ a₂ a₃..... nazywamy ułamkiem dziesiętnym nieskończonym. Wśród ułamków dziesiętnych nieskończonych wyróżniamy ułamki okresowe, tzn. takie, których cyfry od pewnego miejsca po przecinku otrzymujemy powtarzając tę samą grupę cyfr ,zwana okresem ułamka dziesiętnego nieskończonego. Np. 0,111... = 0,(1);ujęcie w nawias cyfry lub grupy cyfr przy zapisywaniu ułamka okresowego oznacza,że będzie się ona dalej powtarzać. Każdy ułamek okresowy przedstawia liczbę wymierną, tzn. suma podanego wyżej szeregu liczbowego jest liczbą wymierną. Prawdziwe jest również twierdzenie odwrotne: każda liczba wymierna może być przedstawiona w postaci ułamka okresowego. Wynika stąd ,że ułamek dziesiętny nieskończony , który nie jest okresowy, przedstawia liczbę niewymierną. Każda liczba niewymierna może zostać przedstawiona w postaci ułamka dziesiętnego nieskończonego, który nie jest okresowy.

ułamek łańcuchowy (ułamek ciągły) : Wyrażenie postaci

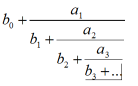
.Ułamki a₁ / b₁, a₂ / b₂,... nazywamy odpowiednio pierwszym, drugim, ... ogniwem ułamka łańcuchowego, liczby całkowite a₁ ,a₂ cząstkowymi licznikami ,zaś liczby całkowite b₁, b₂ cząstkowymi mianownikami (b_n ≠ 0, n = 1,2,...). Ułamek łańcuchowy nazywamy skończonym ,jeśli ciąg ogniw a_n / b_n jest skończona, zaś nieskończonym w przypadku przeciwnym. Ułamek łańcuchowy skończony przedstawia liczbę wymierną ,zaś nieskończony (wartość jego określamy jako granicę, do której dąży ułamek łańcuchowy skończony, utworzony z pierwszych n jego ogniw, gdy n -> ∞) liczbę niewymierną i może być pomocny przy wyznaczaniu jej przybliżenia wymiernego. Ułamki łańcuchowe wprowadził R.Bombelli (1572), zaś algorytmy rachunkowe będące w ścisłym związku z ułamkiem łańcuchowym znane już były matematyką starożytności (np. przybliżenia liczb niewymiernych wyznaczone przez Archimedesa).W ostatnich czasach ułamki łańcuchowe mają ponownie duże znaczenie, m.in. w związku z obliczeniami przybliżonymi na maszynach matematycznych.

ułamek nieprzywiedlny (nieskracalny) : Ułamek zwykły a/b, w którym liczby naturalne a i b są liczbami względnie pierwszymi. Np 2/3 i 2/5 są ułamkami nieskracalnymi, zaś 4/6 nie jest ułamkiem nieskracalnym, ponieważ liczby 4 =2*2 i 6 = 2*3 mają wspólny dzielnik.

ułamek niewłaściwy : Ułamek, którego wartość bezwzględna jest co najmniej równa jedności ,np. 2/2, 4/3, 5/4 ,2.12 itd są ułamkami niewłaściwymi.

ułamek okresowy : ułamek dziesiętny nieskończony

ułamek właściwy : Ułamek co do wartości bezwzględnej mniejszy od jedności,np. 1/3, 1/2, 0.62

ułamek zwykły : Ułamek postaci a/b, gdzie z i b są liczbami naturalnymi lub ogólniej całkowitymi (b ≠ a).Działania arytmetyczne na ułamkach zwykłych przeprowadzamy według następujących zasad:
I. a/b+c/d = ad+bc / bd
II. a/b-c/d = ad-bc / bd
III. a/c*c/d=ac/bd
IV.a/b:c/d = a*d/b*c

undecylion : Nazwa liczby 10⁶⁶

Urbanik Kazimierz (1930-2005) : Matematyk polski, profesor Uniwersytetu Wrocławskiego, członek PAN, autor prac z rachunku prawdopodobieństwa, analizy funkcjonalnej, algebry, fizyki teoretycznej, współtwórcza tzw. procesów stochastycznych uogólnionych