walec : powierzchnia walcowa

Wallis John (1616-1703) : Matematyk i teolog angielskim profesor geometrii w Oksfordzie jeden z założycieli Royal Society, autor dzieła "Arithmetica infinitorum", w którym rozpatruje szeregi nieskończone, prac o stożkowych, operuje pojęciem nieskończoności i nieskończenie małych, choć w sposób niezbyt ścisły, zbliża się do pojęcia granicy. Wallis wprowadził symbol ∞ dla oznaczenia nieskończoności. Prace Wallisa przygotowały w pewnym stopniu grunt pod powstanie rachunku różniczkowego i całkowego.

Walras Leon (1834-1910) : Ekonomista francuski, założył tzw. matematyczną szkołę w ekonomii, stworzy matematyczną teorię ogólnej równowagi ekonomicznej.

wariacje bez powtórzeń : Pojęcie kombinatoryki. Wariacjami bez powtórzeń nazywamy kombinacje utworzone z n elementów (przedmiotów) branych po m ≤ n, które różnią się od siebie bądź samymi elementami bądź ich kolejnością. Np. wybierając po 2 litery (tzn. m= 2)spośród trzech: a,b i c (tzn n = 3), można utworzyć 6 wariacji bez powtórzeń : ab, ac,bc,ba,ca,cb. Ogólnie, liczba wariacji bez powtórzeń z n przedmiotów branych po m ≤ n na raz wynosi
.

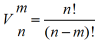wariacje z powtórzeniami : Pojęcie kombinatoryki .Wariacjami z powtórzeniami nazywamy kombinacje utworzone z n elementów (przedmiotów) branych po m na raz, które różnią się od siebie bądź samymi elementami bądź ich kolejnością, przy czym ten sam element może występować wielokrotnie (powtarzać się).Np. wybierając po 2 litery (m = 2) spośród trzech : a,bi c (n = 3), można utworzyć 9 = 3² wariacji z powtórzeniami : aa,ab,ac,bb,bc,bc,cc,ca,cb. Ogólnie, liczba wariacji z powtórzeniami z n przedmiotów branych po m na raz wynosi
.

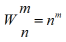warszawska szkoła matematyczna : Ośrodek matematycznej myśli naukowej skupiony wokół Uniwersytetu Warszawskiego. Pierwszymi profesorami matematyki na odrodzonym po I wojnie światowej Uniwersytecie Warszawskim w 1919 byli Stefan Mazurkiewicz, Zygmunt Janiszewski i Wacław Sierpiński. Ich to wraz z grupą uczniów (Kuratowski, Saks, Tarski,Knaster, Zygmund , Marczewski,Borsuk,Zarankiewicz,Charzyński,Wakulicz i in.) należy uważać za twórców tzw. warszawskiej szkoły matematycznej. Dużą rolę odegrało wydawane z inicjatywy prof. Janiszewskiego od 1920 czasopismo matematyczne Fundamenta Mathematicae. Warszawska szkoła matematyczna ma osiągnięcia na skalę światową w zakresie teorii mnogości, topologi oraz logiki. Od utworzenia Państwowego instytutu Matematycznego w 1948 działalność warszawskiej szkoły matematycznej jest ściśle z nim związana.

wartość bezwzględna : bezwzględna wartość

wartość przeciętna (esperancja,wartość oczekiwana, wartość średnia) : W rachunku prawdopodobieństwa średnia wartość zmiennej losowej, jakiej należy oczekiwać przy nieograniczonym kontynuowaniu losowań. Jeżeli zmienna losowa X przyjmuje wartości x₁,x₂,...,x_n z odpowiednimi prawdopodobieństwami p₁,p₂,...,p_n to wartość przeciętna tej zmiennej , oznaczana symbolem E(X), wyraża się wzorem : E(X) = x₁*p₁+x₂*p₂+...+x_n*p_n.

warunek dostateczny (wystarczający)pewnego faktu matematycznego : Każdy warunek, z którego fakt ten wynika. Np. warunek dostateczny podzielności liczby naturalnej przez 5 jest jej podzielność przez 10; innym warunkiem dostatecznym tego samego faktu jest podzielność liczby przez 20, jeszcze innym, aby ostatnia cyfra w zapisie tej liczby byłą 0 lub 5. Jeżeli jakikolwiek warunek dostateczny pewnego faktu jest spełniony, to możemy twierdzić ,że fakt ten zachodzi;jeżeli jednak pewien warunek dostateczny nie jest spełniony, to fakt z nim związany może zarówno zachodzić jak i nie. Np .jeżeli liczba nie dzieli się przez 10, to nie wynika stąd ,że nie dzieli się przez 5, choć podzielność przez 10 jest warunkiem dostatecznym podzielności przez 5.

warunek konieczny pewnego faktu matematycznego : Każdy wniosek wypływający z tego faktu. Np. warunek konieczny podzielności liczby naturalnej przez 8 jest podzielność tej liczby przez 4, innym warunkiem koniecznym jest podzielność przez 2, czyli parzystość. Jeżeli warunek konieczny pewnego faktu jest spełniony, to nie możemy na podstawie tego faktu twierdzić ,że fakt ten zachodzi; jeżeli jednak warunek konieczny nie jest spełniony, to fakt na pewno nie zachodzi. Np. jeśli liczba jest podzielna przez 4 (co jest warunkiem koniecznym podzielności przez 8), to może nie być podzielna przez 8, jeśli jednak liczba nie jest podzielna przez 4 , to nie jest podzielna przez 8.

Ważewski Tadeusz (1896-1972) : Matematyk polski, profesor Uniwersytetu Jagiellońskiego ,członek PAN, zajmował się równaniami różniczkowymi.

Weierstrass Karl Teodor Wilhelm (1815-1897) : Matematyk niemiecki, profesor Uniwersytetu Berlińskiego, gdzie wykładał przez 30 lat. Większość prac Wierestrassa została wydana dopiero po jego śmierci. Weierstrass opracował logiczne postawy analizy matematycznej .Dążył do wyeliminowania z analizy matematycznej rozważań geometrycznych, starając się sformalizować wszelkie rozwiązania .Weirestrass jest jednym z twórców nowoczesnych ścisłych metod matematycznych .Wiele prac Weirestrassa dotyczy również funkcji analitycznych i rachunku wariacyjnego.

wektor : Odcinek prostej łączącej dwa punkty, w którym wyróżniony jest pewien kierunek,mianowicie jeden koniec odcinka A jst początkiem wektora a drugi B końcem. Jeżeli początek wektora pokrywa się z końcem, to wektor nazywamy zerowym. W fizyce używamy wektorów do opisu wielkości kierunkowych (np. prędkość, przyspieszenie ,siła). Wektor oznaczamy używając liter ze strzałkami 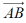lub kreskami 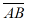;jeżeli nie powoduje to pomyłek, można kreski (strzałki) opuścić. Wektor na osi jest wektorem w przestrzeni jednowymiarowej .Liczbę

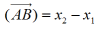
nazywamy miarą względną wektora, natomiast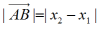

nazywamy miarą bezwzględną wektora na osi. Na płaszczyźnie każdemu wektorowi przyporządkowujemy parę liczb - miary względne rzutów wektora na osie, które nazywamy składowym wektora

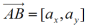
, gdzie
;
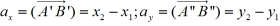analogicznie w przestrzeni trójwymiarowej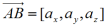

Rozróżniamy trzy pojęcia wektora: 1.wektor swobodny - klasa wektorów równoległych o tej samej długości i zwrocie (dane są np. tylko składowe wektora);2.wektor ślizgający się - klasa wektorów leżących na jednej prostej, o tej samej długości i zwrocie (np. dane są składowe wektora i prosta po której wektor się ślizga);3.wektor związany - jeden wektor (dane są np. składowe wektora oraz jego punkt zaczepienia, tzn, punkt początkowy lub końcowy). Długością wektora nazywamy długość odcinka łączącego punkt początkowy i końcowy; wyraża się ona wzorem:

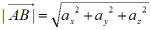
dwa wektory niezerowe nazywamy równoległymi (kolinearnymi), jeżeli leżą na prostych równoległych lub na jednej prostej. Wektor zerowy jest równoległy do każdego wektora. Jeśli odcinki AC i BD nie przecinają się , to ich wektory są zgodnie równoległe, jeżeli przecinają się to przeciwrównoległe .Wersorami osi nazywamy wektory o kierunku osi współrzędnych i długości jednostkowej (wektory jednostkowe) Wersory osi najczęściej oznaczone są literami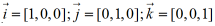
.
w klasie wektorów swobodnych określone są następujące pojęcia i działania algebraiczne (tzw. algebra wektorów): 1.Dwa wektory niezerowe są równe, jeżeli są zgodnie równoległe i mają tę samą długość. 2.Suma wektorów (wypadkowa) b = a₁+a₂+...+ a_n jest wektorem otrzymanym w następujący sposób: z punktu A₁ jako punktu początkowego wykreślamy wektor a₁ z końca, z końca tego wektora A₂ wykreślamy wektor a₂ ,z końca A₃ wektor a₂ wykreślamy wektor a₃ itd. Punkt końcowym A_n+1 ostatniego, wykreślonego wektora a_n jest końcem, a A₁ początkiem wektora zwanego sumą wektorów czyli
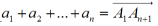. Jest to geometryczny sposób dodawania wektorów; algebraicznie dodając wektory otrzymujemy wektor, którego składowe równają się sumie odpowiednich składowych wektorów , które dodajemy tzn . a+b+c = [a_x,a_y,a_z] + [b_x,b_y, b_z]+ [c_x,c_y,c_z] = [a_x+b_x+c_x , a_y+b_y+c_y , a_z+b_z+c_z ]. 3.Ażeby pomnożyć wektor przez liczbę , mnożymy jego składowe przez tę samą liczbę λ * a = λ* [a_x,a_y,a_z] = [λa_x,λa_y,λa_z], czyli otrzymujemy wektor równoległy do wektora a , lecz λ razy dłuższy. Jeżeli λ > 0 to wektor λ a jest zgodnie równoległy do wektora a, jeżeli &lambda < 0 to wektor &lambda a jest przeciwrównoległy do wektora a. 4.Odejmowanie wektorów sprowadzamy do dodawania a- b = a+(-b), czyli do wektora a dodajemy wektor b z przeciwnym zwrotem. 5.Iloczynem skalarnym wektorów niezerowych a i b nazywamy liczbę (skalar) określoną wzorem a*b = |a| * |b| * cos φ, gdzie φ jest kątem między a i b. Zachodzi również równość a*b = a_x* b_y + a_y* b_y + a_z* b_z>Tę ostatnią równość możemy uważać za definicję iloczynu skalarnego; wtedy równość poprzednia będzie twierdzeniem. 6.Iloczynem wektorowym dwóch wektorów niezerowych a i b nazywamy trzeci wektor c = a x b (iloczyn wektorowy w odróżnieniu od skalarnego oznaczamy znakiem X) spełniający warunki: 1) wektor c jest prostopadły do wektorów a i b; 2) długość wektora c jest określona wzorem |c| = |a| * |b| * sin φ (długość iloczynu wektorowego równa się liczbowo polu równoległoboku o bokach, których długość równają się długości wektorów a i b);3.trójka w a,b,c jest zgodnie zorientowana z układem osi współrzędnych, tzn. w układzie współrzędnych lewoskrętnym (prawoskrętnym) wektory a,b,c tworzą układ lewoskrętny (prawoskrętny). Iloczyn wektorowy można wyrazić również za pomocą wyznacznika

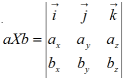
Z definicji iloczynu wektorowego wynika ,że a x b = -(b x a); 4. wektory a,b,c ... nazywamy liniowo zależnymi, jeżeli istnieją takie liczby α, β, γ ... nie równe jednocześnie zeru, ze liniowa kombinacja tych wektorów α a + β b + γ c jest wektorem zerowym.

wektorfunkcja : funkcja wektorowa

wektory ortogonalne : wektory prostopadłe

wektor osi : wektor

Wessel Caspar (1745-1818) : Matematyk duński, z zawodu mierniczy, geodeta,napisał pracę poświęconą teorii wektorów na płaszczyźnie i w przestrzeni trójwymiarowej, w której podaj po raz pierwszy pełną geometryczną konstrukcję liczb zespolonych

Weyl Herman (1885-1955) : Matematyk niemiecki, profesor politechniki w Zurychu i uniwersytetów w Getyndze i Princestone (USA), autor prac z teorii funkcji, teorii grup, geometrii różniczkowej i fizyki matematycznej

Whitehead Alfred North (1861-1947) : Matematyk i filozof angielski, wykładał matematykę na uniwersytecie w Cambridge, Londynie i na uniwersytecie harvardzkim (USA).Wraz a B.Russelem napisał "Principia Mathematica" (Podstawy matematyki)

wielobok : wielokąt

wielokąt : Część płaszczyzny ograniczona zwykłą linią łamaną zamkniętą; boki linii łamanej nazywamy bokami wielokąta, a jej wierzchołki - wierzchołkami wielokąta. Czasem wprowadzamy bardziej ogólne pojęcie wielokąta : wielokąt jest to krzywa otrzymana przez połączenie n punktów (n ≥3) odcinkami , przy czym każdy punkt jest końcem dokładnie dwóch odcinków (punkty mogą nie leżeć w jednej płaszczyźnie).Rozważmy również takie wielokąty, których boki przecinają się wzajemnie. Wielokąty możemy nazwać spójną częścią płaszczyzny (obszar spójny - obszar, w którym każe dwa punkty, dadzą się połączyć łamaną całkowicie leżącą w tym obszarze) ograniczoną skończoną liczbą liczbą odcinków. Wielokąt nazywamy również wielobokiem. Suma kątów wewnętrznych wielokąta płaskiego o n bokach nie przecinających się ze sobą wynosi (n-2) 180^o .Wielokątem wypukłym nazywamy wielokąt ograniczony linią łamaną wypukłą zamkniętą (każda prosta, na której leży bok wielokąta, nie przecina innych boków wielokąta; każde dwa punkty wewnętrzne można połączyć odcinkiem leżącym wewnątrz wielokąta). Wielokąt niewypukły, ograniczony linią łamaną zwykła, której boki nie przecinają się , nazywamy wklęsłym. Katem wewnętrznym wielokąta wypukłego nazywamy każdy kąt wypukły wyznaczony przez dwa boki wychodzące z jednego wierzchołka. Kątem zewnętrzny wielokąta nazywamy kąt dopełniający kata wewnętrznego .Punkty leżące wewnątrz wielokąta nazywamy punktami wewnętrznymi wielokąta a leżące na zewnątrz - punktami zewnętrznymi. Odcinek łączący dwa wierzchołki wielokąta nie leżące na jednym boku nazywamy przekątną wielokąta. Wielokąt wypukły o n bokach ma (n-3)n/2 przekątnych .Wielokątami są trójkąty, czworokąty, równoległoboki i in.

wielokąt foremny : Wielokąt o wszystkich bokach i kątach wewnętrznych równych; wielokąt foremny jest wielokątem wypukłym. W starożytności znana była konstrukcja wielokąta foremnego przy pomocy cyrkla i linijki w przypadku danego boku lub promienia okręgu opisanego na wielokącie foremnym o liczbie boków równej 3*2ⁿ,4*2ⁿ, 5*2ⁿ, 3*5*2ⁿ gdzie n oznacza liczbę naturalną lub zero. W 1801 C.Gauss dowiódł ,ze konstrukcję taką można wykonać tylko wtedy , kiedy liczba bokó równa jest m = 2ⁿ*p₁*p₂*,...*p_k, gdzie p₁,p₂,...,p_k są liczbami pierwszymi Gaussa tzn. liczbami postaci p = 2^2r + 1 ( r -liczba naturalna); znamy na razie pięć przypadków takich liczb : 3,5,17,257,65337. Konstrukcję tę możemy zatem wykonać tylko dla m = 3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40..., nie można jej natomiast wykonać dla m = 7,9,11,13,14,18,19,..... Istnieją również wielokąty foremne wklęsłe o bokach równych i przecinających się (zaczynając od pięciokąta), gdzie każdy bok następny nachylony jest do poprzedniego pod tym samym kątem i w tym samym kierunku.

wielokąty podobne : Wielokąty, które mają taką samą liczbę boków, odpowiednie kąty równe i odpowiednie boki proporcjonalne.

wielokrotność liczby naturalnej a : Liczba naturalne b, która dzieli się przez a bez reszty. Np. 64 jest wielokrotnością 8, bo 64 : 8 = 8, jest także wielokrotnością liczb 2,4,16 i 32 nie jest zaś wielokrotnością liczby 6 .Wspólną wielokrotnością liczb naturalnych a,b...,c nazywamy taką liczbę naturalną n, która dzieli się bez reszty przez każdą z nich;najmniejszą z liczb o tej właściwości nazywamy najmniejszą wspólną wielokrotną (NWW) liczb a,b,...,c .Wyznaczenie NWW sprowadza się do rozkładania danych liczb na czynniki pierwsze (jeśli nie są to liczby pierwsze),co pozwala już na łatwe wypisanie wszystkich czynników NWW .Inną metodę znajdowania NWW daje wzór
NWW(a,b) = a*b / nwd(a,b) (największy wspólny dzielnik). Wyznaczanie NWW jest ważne przy sprowadzaniu ułamków do wspólnego mianownika, gdyż pozwala wykonać rachunek przy pomocy możliwie małych liczb.

wielomian : Suma jednomianów np. 3xy²-z³ + 2yz+5 jest wielomianem zmiennych x,y i z. Wielomian o postaci axc+b, ax²+c ,ax³+bx²+cx+d, ogólnie a_nxⁿ + a_n-1x^n-1+...+a₁x+a₀ gdzie a₀,a₁,..,a_n (a_n ≠ 0) są to określone liczby , tzw. współczynniki wielomianu, zaś x oznacza zmienną, jest wielomianem jednej zmiennej i oznacza się go symbolem W_n(x), przy czym n nazywamy stopniem wielomianu. Wielomian W(x) jest funkcja zmiennej x określoną dla każdej wartości tej zmiennej, Dwa wielomiany nazywamy równymi wtedy i tylko wtedy , jeśli mają jednakowe współczynniki przy odpowiednich potęgach (różnią się więc co najwyżej kolejnością składników).Wielomiany można dodawać i odejmować. Wielomiany mnożymy mnożąc każdy składnik mnożnej przez każdy składnik mnożnika, a następnie redukując wyrazy podobne

wielościan : Część przestrzeni ograniczona powierzchnią wielościanu wraz z punktami leżącymi na tej powierzchni. Wielokąty tworzące powierzchnię wielościanu nazywamy ścianami wielościanu, wierzchołki tych wielokątów - wierzchołkami wielościanu, a boki wielokątów - krawędziami wielościanu .Odcinek łączący dwa wierzchołki wielościanu nie leżące na jednej ścianie nazywamy przekątną wielościanu .Wielościan nazywamy wypukłym, jeżeli każde dwa jego punkty można połączyć odcinkiem całkowicie leżącym wewnątrz tego wielościanu. Można też podać inną definicję : wielościanem wypukłym nazywamy wielościan ,który leży po jednej stronie każdej z płaszczyzn, na których leżą ściany tego wielościanu .Wielościan który nie jest wypukły nazywamy wklęsłym. Dwie ściany wielościanu wypukłego leżące w płaszczyznach równoległych nazywamy przeciwległymi. Dwie ściany wielościanu o wspólnej krawędzi nazywamy przyległymi Dwa wielomiany nazywamy podobnymi , jeżeli mają taką samą liczbę ścian, odpowiadające sobie są wielokątami podobnymi, a odpowiednie katy dwuścienne są sobie równe .Dla wielościanu wypukłego zachodzi równość W-K+S=2, gdzie W - liczba wierzchołków, K - liczba krawędzi, S - liczba ścian (twierdzenie Eulera) .Jeżeli a jest liczbą kątów wielościanu wypukłego to zachodzą zależności : A =2K, A ≥ 3S, W ≤ 2/3 K, S ≤ 2/3 K, S ≤ 2W-4. Wielościan posiada co najmniej 4 ściany. Wielościan o 4 ścianach nazywamy czworościanem 0 5 - pięciościanem itd.

wielościan foremny : Wielościan wypukły, którego wszystkie ściany są jednakowymi wielokątami foremnyi i w każdym wierzchołku zbiega się jednakowa liczba ścian. Wielokątów foremnych jest 5: czworościan foremny ,sześcian, ośmiościan, dwunastościan i dwudziestościan. W każdy wielokąt foremny można wpisać kulę i opisać na nim kulę. Punkty styczności ścian wielokąta foremnego z powierzchnią kuli wpisanej w ten wielokąt foremny wyznaczają inny wielościan foremny. Kula wpisana w czworościan foremny wyznacza w ten sposób inny czworościan, z sześcianu otrzymujemy ośmiościan, s ośmiościanu sześcian, z dwunastościanu - dwudziestościan, dwudziestościanu - dwunastościan

Wiener Norbert (1894-1964) : Matematyk amerykański. Prace Wienera dotyczą podstaw matematyki, rachunku prawdopodobieństwa i analizy funkcjonalnej. Wiener jest najwybitniejszym inicjatorem badań cybernetycznych.

wierzchołek paraboli : parabola

wierzchołek pęku prostych : pęk prostych

wierzchołki elipsy : elipsa

Wilkosz Witold (1891-1941) : Matematyk, filozof i logik polski, profesor Uniwersytetu Jagiellońskiego, autor prac naukowych i podręczników, wybitny popularyzator.

Witelusz, Witello,Vitell (ok. 1225-ok.1290) : Pierwszy znany polski matematyk, fizyk i filozof, zajmował się krzywymi stopnia drugiego, skonstruował przyrządy do kreślenia niektórych krzywych. W badaniach optycznych posługiwał się trygonometrią

wniosek z twierdzenia : Nowy fakt matematyczny wynikający z tezy danego twierdzenia w sposób prosty i bezpośredni na tyle ,że zbędne jest przeprowadzanie specjalnego dowodu tego faktu tego faktu.

Wroński Hoene : Hoene -Wroński

wskaźnik : indeks

wspólna wielokrotność dwu liczb naturalnych m i n : Każda liczba naturalna podzielna przez m i n

współczynnik kątowy : linia prosta

współczynnik proporcjonalności : proporcjonalność prosta

współczynnik wielomianu : wielomian

współmierność odcinków : odcinek

współrzędne : układ współrzędnych

wstęga Möbiusa : powierzchnia jednostronna

wycinek kołowy : okrąg

wycinek kuli : Część kuli (powierzchnia kulista) ograniczona powierzchniami bocznymi dwóch współosiowych stożków o wspólnym wierzchołku w środku kuli .W szczególnym przypadku, kiedy jeden stożek redukuje się do prostej, wycinek kuli ograniczony jest powierzchnią boczną stożka i częścią powierzchni kuli. Objętość wycinka kuli V = 2/3* πr² * h , gdzie r oznacza promień kuli; h= O₁O₁

wykładnik potęgi : potęga

wykres funkcji : Graficzne przedstawienie przebiegu jej zmienności. Jeżeli funkcja y = f(x) określona jest wzorem, to dla wybranych dostatecznie gęsto wartości x obliczamy wartości y notując je w tabelce zmienności. Następnie zaznaczamy w układzie współrzędnych Oxy punkty odpowiadające parom liczbowym (x,y) odczytywanym z tabelki; otrzymamy różne punkty wykresu funkcji. Gdybyśmy mogli w ten sposób zaznaczyć na płaszczyźnie Oxy wszystkie punkty odpowiadające parom (x,y) określonym zależnością y = f(x) to utworzyłyby one zbiór punktów zwany wykresem funkcji; wykres ten otrzymamy w przybliżeniu, łącząc odręczne (lub za pomocą odpowiedniego krzywika) kilka zaznaczonych jego punktów.

wypadkowa wektorów : wektor

wypukłość i wklęsłość krzywej : Własność krzywej polegająca na tym ,że leży ona ponad (nad) każdą swoją styczną. Niech funkcja f(x) posiada w rozważanych przedziałach drugą pochodną ciągłą. warunkiem wystarczającym wypukłości (wklęsłości) krzywej będącej wykresem funkcji f(x) w przedziale (a,b) jest f′′(x) < 0 [dla wklęsłości f′′(x) > 0]

wyraz ogólny ciągu : ciąg

wyraz wolny (w równaniu) : Składnik, który nie zawiera niewiadomej (zmiennej). Np. w równaniu ax² + bx + c = 0, współczynnik c jest wyrazem wolnym.

wyrażenie algebraiczne : Zapisane za pomocą cyfr i liter wyniki czterech działań arytmetycznych oraz pierwiastkowania. Jeżeli na miejsce liter w wyrażeniu algebraicznym podstawimy określone liczby i wykonamy wskazane działania, to otrzymamy liczbę zwaną wartością liczbową danego wyrażenia algebraicznego.

wyrażenia nieoznaczone : Symbole 0/0 , ∞ / ∞ , ∞ - &infine; 0^∞ , ∞⁰ , 0⁰, 1^∞ nie mające określonych wartości liczbowych a służące niekiedy do opisywania w skróceniu pewnych faktów matematycznych związanych z wielkościami niekończenie małymi i nieskończenie wielkimi.

wyrażenia niewymierne : Wyrażenia algebraiczne , w których występuje pierwiastkowanie

wyrażenie wymierne : Wyrażenie algebraiczne , w kórych występuje jedynie działanie algebraiczne, np. a² -b/a+b

wyróżnik równania kwadratowego : równanie kwadratowe

wyróżnik równania trzeciego stopnia : równanie trzeciegpo stopnia

wyznacznik (det.A) : Wyrażenie utworzone z elementów macierzy kwadratowej A o n wierszach i n kolumnach (n ≥ 2),zgodnie z następującym wzorem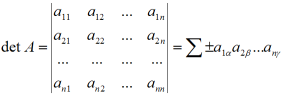

gdzie sumowanie Σ jest rozciągnięte na wszystkie permutacje &alpja;, β,... γ liczb 1,2,...,n, przy czym znak "+" bierze się w przypadku, gdy w danej permutacji liczba większa poprzedza parzysta liczbę razy (bądź nigdy) liczbę mniejszą, ząs znak "-" w przypadku przeciwnym. Wartość wyznacznika nie ulega zmianie, gdy przestawimy jego wiersze z kolumnami w ustalonym porządku (tzn. pierwszy wiersz na miejscu pierwszej kolumny, drugi na miejscu drugiej, itd.)Wyznacznik zmienia znak na przeciwny, gdy zmieniamy miejscami dwa jego wiersze (lub dwie kolumny),wyznacznik jest równy zeru ,gdy elementy jego dwóch wierszy (lub kolumn) są proporcjonalne itd. Wyznaczniki wprowadzone zostały pod koniec XVIII wieku i na początku XIX wieku w pracach Cramera, Vandermonde`a, Laplace`a, Cauchy`ego, Gaussa( który używał nazwy determinant, stąd skrót det) i Jacobiego, głownie przy badaniu układów równań pierwszego stopnia, dzięki którym nabiera ono szczególnej harmonii i przejrzystości.

wyznacznik układu n równań pierwszego stopnia o n niewiadomych x₁,x_n,...,x_n : a₁₁x₁+a₁₂x₂+...+a_1nx_n = c₁ ;a₂₁x₁+a₂₂x₂+...+a_2nx_n = c₂ ;.............;a_n1x₁+a_n2x₂+...+a_nnx_n = c_n. Wyznacznik D utworzony z macierzy współczynników przy tych niewiadomych
. Jeżeli D ≠ 0 to układ równań posiada dokładnie jedno rozwiązanie dane wzorami Cramera

wyznacznik Vandermonde`a V<sub>n</sub> stopnia n ≥ 2 : Wyznacznik o następującej budowie
.
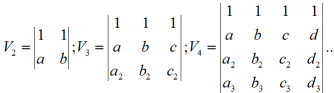Wartość wyznacznika Vandermonde`a równa się iloczynowi różnic elementów drugiego wiersza :V₂ = b-a , V₃ = (c-b) (c-a)(b-a), V₄ = (d-c)(d-b)(d-a)(c-b)(c-a)(b-a).

wzniesienie : depresja

wzory Cardana : równanie trzeciego stopnia

wzory Cramera : Wzory na rozwiązywanie układu n równań liniowych o n niewiadomych (n ≥ 2) wyrażone za pomocą wyznaczników, w przypadku gdy wyznacznik tego układu jest różny od zera.

wzory Gaussa : Zależności pomiędzy bokami,b,c (w mierze łukowej) i kątami α, β;γ trójkąta sferycznego:

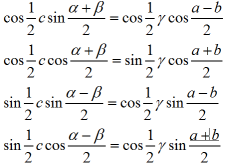
Wzory Gaussa są również nazywane analogiami Delambre`a

wzory redukcyjne : Wzory pozwalające wyrazić funkcje trygonometryczne kąta dowolnego przez funkcje trygonometryczne kąta ostrego lub nawet kąta zawartego w przedziale [0, 45^o]. Wzory redukcyjne możemy podzielić na dwie grupy: takie , kiedy funkcje trygonometryczne przechodzą na kofunkcje i takie kiedy pozostają niezmienione :

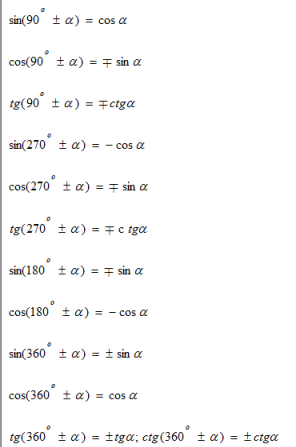
Wzory redukcyjne łatwo zapamiętać dzięki ich właściwościom; jeżeli we wzorze redukcyjnym występuje kąt 90^o lub 270^o , to funkcja przechodzi na kofunkcję, tzn. otrzymuje lub traci przedrostek co; jeżeli kąt wynosi 180^o lub 360^o , to funkcja pozostaje niezmieniona .Znak po prawej stronie ustalamy na podstawie wartości funkcji występującej po lewej stronie.

wzory skróconego mnożenia : Potoczna ,niezbyt zgrabna nazwa następujących wzorów algebry elementarnej:
(a+b)(a-b) = a² + b²,(a±b)² = a²±2ab+b²; (a+b)(a²-ab+b²) = a³ + b³;(a-b)(a²+ab+b²)= a³-b³;(a±b)³ = a³±3a²b+3ab² ±b³

wzory Viete`a : równanie algebraiczne

wzór Carnota : twierdzenie cosinusów

wzór cosinusów : twierdzenie cosinusów

wzór Eulera : Podany w 1743 wzór wyrażający związek funkcji wykładniczej o wykładniku urojonym z funkcjami trygonometrycznymi:
e^ix = cos x + i sin x. Konsekwencje wzoru Eulera są następujące zależności :
cos x = e^ix + e^-ix / 2 = cosh (ix), sin x = e^ix - e^-ix / 2i = i sinh (ix)
. Wzór Eulera odgrywa ważną rolę w wielu działach techniki, szczególnie tam gdzie analizuje się drgania (mechaniczne lub elektryczne)

wzór Herona : Wzór wyrażający zależność między polem trójkąta S a jego bokami a,b,c:
,
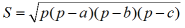gdzie 2p=a+b+c. Wzór Herona ma duże znaczenie praktyczne , pozwala bowiem obliczyć pole trójkąta bez znajomości jego wysokości, co np. przy mierzeniu gruntów byłoby praktycznie niewykonalne.

wzór interpretacyjny Lagrnage`a : Podany w latach 1792-1793 wzór pozwalający wyznaczyć wielomian W_n (x), który dla danych n+1 wartości x₀ < x₁ < x₂.... < x_n zmiennej x przyjmuje z góry zadane wartości y₀,y₁,y₂,...,y_n

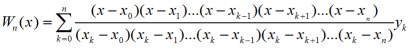
wzór interpolacyjny Newtona : Podany przez Gregory`ego zaś nazwany wzorem interpolacyjnym Newtona około1 1676 roku wzór pozwalający wyznaczyć wielomian W_n(x), który dla danych n+1 wartości x₀,x₁ = x₀+h,..., x_n = x₀+n*h (h > 0) zmiennej x przyjmuje z góry dane wartości y₀,y₁,y₂,...,y_n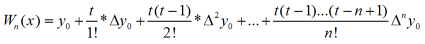
, gdzie t = x-x₀ / h, Δy₀ = y₁-y₂, Δy₁ = y₂-y₁,..., zaś Δ^ky_i = Δ^k-1y_i+1 - Δ^k-1y_i

wzór Leibniza : Wzór na pochodną n-tego rzędu iloczynu dwóch funkcji u(x) i v(x):

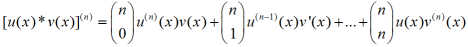
wzór Maclaurina : Szczególny przypadek wzoru Taylora. Jeżeli funkcja f(x) posiada w otoczeniu punktu x = 0 n pochodnych, to dla której wartości x z tego otoczenia zachodzi wzór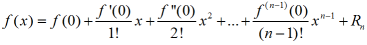
zwany wzorem Maclaurina, przy czym R_n, tzw. reszta we wzorze Maclaurina, wyraża się wzorem R_n = f⁽ⁿ⁾(c) / n! * xⁿ, gdzie c jest zawarte między 0 a x

wzór Moivre`a : Podany w 1707 wzór na potęgowanie liczb zespolonych przedstawionych w postaci trygonometrycznej [r(cos φ + i sin φ)] ⁿ = rⁿ(cos n φ + i sin nφ)

wzór podstawowy rachunku całkowego : rachunek całkowy

wzór Regiomontana : wzór tangensów

wzór rekurencyjny : Wzór służący do wyznaczania wyrazów pewnego ciągu, który uzależnia wartość ogólnego wyrazu tego ciagu od wartości poprzedzających go wyrazów.

wzór Simpsona : przybliżone całkowanie

wzór sinusów : twierdzenie sinusów

wzór Stirlinga : Wzór dotyczący silni. Wzór Stirlinga ma postać

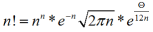
gdzie 0 < Θ < 1 i znajduje zastosowanie w wielu działach matematyki, pozwalając na przybliżone obliczanie i ocenę silni dla dużych wartości n.

wzór tangensów : Zależność między bokami i katami trójkąta. Jeżeli a,b,c s,a długościami boków a α, β, γ kątami trójkąta, to zachodzi związek

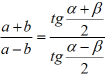
stosowany często w postaci tg α-β / 2 = a-b/a+b * ctg γ/2. Wzór tangensów nazywamy również wzorem Regiomontana; używamy przy "rozwiązywaniu" trójkątów.

wzór Taylora : Przedstawienie funkcji f(x) w postaci sumy wielomianu i składnika zwanego resztą. Jeżeli funkcja f(x) posiada w otoczeniu punktu x = a n pochodnych, to dla każdej wartości z z tego otoczenia zachodzi wzór

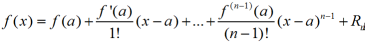
zwany wzorem Taylora, przy czym R_n , tzw. reszta we wzorze Taylora, wyraża się wzorem : R_n = f⁽ⁿ⁾(c) /n! * (x-a)ⁿ, gdzie c jest zawarte między a i x. W przypadku a = 0 wzór Taylora nazywa się wzorem Maclaurina.

wzór trapezów : przybliżone całkowanie

wzór Wallisa : Przedstawienie liczby π/2 za pomocą iloczynu nieskończonego
π/2 = 2/1*2/3 * 4/3 * 4/5*6/5*6/7