Systemy Sterowania
W tej części zajmiemy się najbardziej złożonymi elementami. Systemy sterowania mogą być bardzo bogato zdobione ale trudne do zbudowania. Mogą być zbudowane przy użyciu komputerów, elektroniki liniowej ,części mechanicznej, części biologicznych. Ale podstaw wszystkich systemów sterujących jest królowa nauk - matematyka. Biorąc pod uwagę zrozumienie matematyki, możemy oswoić dowolny z tych typów systemów sterujących. W analizie końcowej wszystkie zachowują się w ten sam sposób, podążając za tą samą matematyką. Byłoby herezją dla niektórych, sugerować ,że systemy kontroli mogą być oswojone przez zrozumienie kilku równań, ale faktem jest ,że podstawowe koncepcje matematyczne systemu sterującego mogą być znacznie uproszczone i udostępnione. Jeśli nauczysz się podstaw, możesz prawdopodobnie ekstrapolować na inne przypadki używając swojego instynktu. To jest nasz cel! Systemy sterowania są wszędzie i mogą mieć różne kształty i rozmiary:
• Przeciętny samochód ma w sobie 35 komputerów, napędzających silnik, hamulce, radio, itd.
• Każda toaleta posiada mechanizm sterujący do uzupełniania zbiornika odpowiednią ilością wody i bycia niezawodną
• Średni toster świetnie nadaje się do brązowienia chleba w powtarzalny sposób
• Prawdopodobnie możesz przejść przez całkowicie ciemny pokój, dotykając kilku dobrze znanych kamieni milowych, wyciągnij rękę i znajdź włącznik światła prawie za każdym razem .
Wszyscy uznajemy takie istniejące systemy sterujące za oczywiste. Załóżmy ,że zbudowaliśmy już duże, silne ciało robota z mocą, zwinnością, siłą, prędkości i zręcznością, które uważamy za potrzebne. Teraz nadchodzi trudna część. Oto lista marzeń niematerialnych , które może być naprawdę przyjemne w robocie:
• Inteligencja
• Mądrość
• Współczucie
• Miłość
• Percepcja
• Umiejętności komunikacyjne
Ta długa lista ,z wieloma krytycznymi charakterystykami (które powinna posiadać dobra "osoba") została przerwana. Ile z tych rzeczy powinien mieć robot? Carl Sagan, znany astronom i autor, skomentował kiedyś moc intelektualną nieodłączną w systemie sterowania sondy międzyplanetarnej. Powiedziała ,że komputer sondy był intelektualnym odpowiednikiem krykieta. Słowo o ostrożności. Jeśli masz nadzieję zbudować maszynę z mądrością i współczuciem, masz przed sobą wielkie, niemożliwe zadanie. Oto kilka z głębokich problemów z jakimi będziesz musiał się zmagać. Zachęcamy do rozważenia każdego z nich i zagłębienie się w przyczyny tych problemów i ich konsekwencje
• Prawdą jest ,że ludzki mózg zdolny jest do masowych obliczeń, znacznie więcej niż przeciętny ogromny komputer. Jeśli w to wątpisz, rozważ grę w szachy, w której ludzie bili komputery "na głowę" od lat. Komputery zaprojektowane do gry w szachy dopiero nadrabiają zaległości. Pamiętaj jednak ,że gra w szachy jest grą, którą komputer może przynajmniej łatwo pojąć, tak aby programiści mogli zoptymalizować te obliczenia. Większość życia jest dużo bardziej złożona niż szachy
• Większość aktów interakcji człowieka prawdopodobnie nigdy nie zostanie zdefiniowana, a tym bardziej nie równa się maszynie. Mądrość, miłość i współczucie przychodzą na myśl
• Umysł ludzki ma głębokie defekty, defekty, które manifestują w codziennie nadawanych wiadomościach. Można się spierać z ewolucyjnego punktu widzenia że ludzkie wady takie jak te wywołujące chciwość i wojnę są nieuniknione. Ponadto można argumentować ,że te defekty nadal przynoszą korzyści gatunkowi ludzkiemu i pomagają się rozmnażać. Może to być kontrowersyjne, ale gdybyśmy chcieli wyhodować takie cechy z ludzi, owady prawdopodobnie wyprą nas wcześniej niż moglibyśmy się spodziewać. Mały eksperyment : gdybyś mógł nacisnąć przycisk i wywołać agresję, chciwość zazdrość i inne podobne wady natychmiast znikające z ludzkiej rasy, czy naprawdę wcisnąłbyś przycisk? Gdybyś mógł wybrać takie cechy dla swojego robota, czy je wbudowałbyś?
• Ludzie nie mogą poznać swoich umysłów, a tym bardziej doskonale je powielić. Nie powstrzyma nas to jednak przed próbami
• Jako kontrargument dla poprzedniego stwierdzenia, należy powiedzieć, że ludziom coraz trudniej jest rozróżniać między ludzkimi a komputerowymi "osobowościami" . Alan M. Turing, brytyjski matematyk zaproponował prosty eksperyment , który przerodził się w okresowy test. Eksperyment, zwany Testem Turinga, rzuca wyzwanie przesłuchującemu, który prowadzi rozmowę z dwiema niewidzialnymi jednostkami ,z których jedna to komputer a drugi to człowiek. Osoba przesłuchująca musi odkryć kto jest kim. Zwycięzca otrzymuje Nagrodę Loebnera
• Kolejny problem, którego nie można, a może nie powinno , rozwiązać, rozważa czy Twój robot powinien być męski , żeński czy bezpłciowy. W każdym razie wariant testu Turinga prosi przesłuchującego o rozróżnienie między mężczyzną a kobietą. Jakie pytania chciałbyś zadać?
• Ludzie nie mogą się ze sobą doskonale komunikować Dana osoba może tylko próbować wypowiadać właściwe słowa , które wpajają jego właściwą ideę w umysł innej osoby. Aby komunikować się werbalnie, formujemy nasze myśli, wypowiadamy je, obserwujemy reakcje drugiej osoby i zmieniamy nasze wypowiedzi na podstawie jego reakcji. Wszystkie te działania nie mogą być doskonale wykonane i zawsze mają niezamierzone rezultaty.
Jeśli napisałeś specyfikację robota (i utrzymałeś ją w prostocie), masz ograniczoną liczbę zadań które robot musi wykonać. Wszystko co musisz zrobić to zbudować robota, który wykona te zadania. Gdzie zaczynamy projektowanie robota, aby mógł robić takie rzeczy? Na początek możemy spojrzeć na naturę analogicznych projektów. Natura obfituje w systemy sterujące godne emulacji. Jednak nasze myśli pełne są wizji antropomorficznych wizji robotów. Pierwszym obrazem który przychodzi ci na myśl jest robot z głową, dwojgiem oczu, dwoma uszami, ustami, dwoma ramionami i tułowiem. Czy jesteśmy zwodzeni przez własne instynkty?
Rozproszone Systemy Sterujące
Pomimo wielu argumentów na rzecz istnienia rozproszonej inteligencji wewnątrz ludzkiego ciała, wyraźnie istnieje centralny system kontroli : mózg. Czy jest to centralny system sterowania jakiego rzeczywiście chcemy? Warto to rozważyć przed wyborem architektury. Rozważmy ławicę śledzi. Pływają one w gigantycznych ławicach, błyskając srebrzyście w głębokim niebieskim świetle oceanu. Kiedy tuńczyk przechodzi do ataku, ławica natychmiastowo skręca, dzieli się i łączy jakby za pomocą magii. To taktyka przetrwania śledzi. Jak one tego dokonują? Każdy śledź po prostu obserwuje swoich czterech najbliższych sąsiadów i reaguje na pozycję, prędkość i ruch. Efekt końcowy na poziomie ławicy jest dramatyczny i skuteczny. Tysiące maleńkich mózgów działa niemal jak jeden, a tuńczyk jest częściowo sfrustrowany. Przy odrobinie szczęścia będą kłopotać krewetki. Ławica śledzi używa
"rozproszonego" systemu sterowania. Ławicą zarządza wspólna wola i wspólne działanie pojedynczych ryb. Rozważmy zalety rozproszonego systemu sterowania:
• Taniość. Poszczególne elementy systemu sterowania są proste i tanie. W tym przypadku musielibyśmy zaprojektować cos prostego, jak śledź , a następnie powielić tysiące razy (uzyskując korzyść skali)
• Niezawodność. Jeśli system zaprojektowano tak aby przetrwał awarię części systemu , kilka porażek go nie zniszczy. Z pewnością nie wszystkie śledzie uciekają przed tuńczykiem. Ławica po prostu zmienia kształt aby "załatać" dziurę po zjedzonym śledziu, a życie toczy się dalej
Rozproszony system sterowania ma też pewne wady
• Komunikacja. Czasami trudno jest się komunikować wszystkim pomiędzy pojedynczymi elementami sterującymi. Śledź po drugiej stronie ławicy nie wie o tuńczyku dopóki jego sąsiad tego nie zasygnalizuje. Sygnał paniki rozprzestrzenia się po ławicy jak fala, ale może być za późno. Ta forma wiedzy naprawdę jest mocą i sprawą życia lub śmierci.
• Moc końcowa. Poszczególne elementy wewnątrz rozproszonego systemu sterowania nie są potężne same w sobie. Chociaż zbiorowa ławica śledzi rozwiązuje problem tuńczyka, jak również każdy człowiek lub komputer, pojedynczy śledź nie może dorównać człowiekowi w matematyce lub rozumowaniu .Rozproszone systemy sterowania są często projektowane w celu rozwiązania konkretnych problemów i nie są tak dobre w rozwiązywaniu problemów ogólnych. Jeśli korzystasz z rozproszonego systemu sterowania, bądź ostrożny, poznając wszystkie problemy z którymi musisz się zmierzyć. Jeśli specyfikacje ulegną zmianie , twój projekt może być skołowany.
Centralne Systemy Sterowania
Rzućmy okiem na scentralizowane systemy sterowania. Z pewnością zrozumienie pojedynczego systemu sterowania jest niezbędne dla zrozumienia rozproszonego systemu sterowania. Większość systemów sterowania opiera się na tych samych podstawowych strukturach sterujących. Przyjrzymy się kliku różnym strukturom, ale chodzi o to ,że ich zachowanie można opisać za pomoc tej samej matematyki.
Sterowanie W Otwartej Pętli
Większość systemów sterowania robotami ma jakiś rodzaj sygnału wejściowego i wyjściowego. Pomiędzy, układ sterowania odpowiada na sygnał wejściowy i zmienia odpowiednio sygnał wyjściowy. Sygnał wejściowy jest generalnie sygnałem sterującym niskiego poziomu. Dwoma przykładami sygnału wejściowego mogą być , sygnał z przycisku zasilania na pilocie telewizora lub napięcie liniowe z obrotowego przełącznika przyciemniania .Zasadniczo w systemie sterowania, urządzenie wykonawcze wzmacnia sygnał i przekształca w sygnał wejściowy. Kiedy osoba naciśnie przycisk zasilania na pilocie telewizora, pilot generuje sygnał podczerwieni, który telewizor interpretuje jako zamknięcie przekaźnika i przekazanie zasilania do obwodów telewizora. W rzeczywistości działają dwa systemy sterowania w otwartej pętli. W systemach sterowania w otwartej pętli informacja ma tendencję do przepływania tylko w jedną stronę. Na przykład, system sterowania wewnątrz pilota nigdy się nie dowie czy telewizor się włączył czy nie. Ponadto przycisk zasilania na pilocie nigdy nie wskazuje czy wiązka podczerwieni została wysłana czy nie. Jeśli palec zasłania optykę, nic się nie dziele, a pilot nie wie że telewizor się nie włączył. Przeprowadźmy eksperyment ilustrujący system sterowania w otwartej pętli wewnątrz ciała. Rzuć okiem na prawo i zlokalizuj obiekt w pokoju. Zapamiętaj gdzie jest a potem wróć do tekstu. Teraz zamknij oczy, wskaż obiekt, próbują położyć palec na obiekcie w polu widzenia. Otwórz oczy a zobaczysz jak blisko jesteś. Zauważysz ,że nigdy nie trafisz dobrze z zamkniętymi oczami. Kiedy otworzysz oczy, zobaczysz ,że Twój palec jest trochę wolny. Błąd nigdy nie znika i jest nazywana błędem stanu ustalonego. Jest to błąd , który utrzyma się długo po tym ,jak system
sterowania ustali ostateczne wyniki i nie będzie dokonywał żadnych dalszych korekt. W równaniach , które rozwiniemy później, zobaczymy błąd stanu ustalonego. Wszystkie systemy sterowania mają ten błąd. Jest to ważny parametr, ponieważ projektując system sterowania, należy utrzymywać błąd stanu stabilnego poniżej dopuszczalnych granic. Możesz wykonać inny eksperyment, jeśli masz ściemniacz w domu. Zaczekaj aż zapadnie ciemność i wyłącz ściemniacz, przez co pokój staje się ciemny. Zamknij oczy a potem włącz ściemniacz do miejsca, w którym uważasz ,że jest minimalny dopuszczalny poziom światła do czytania. Otwórz oczy i zobacz czy zrobiłeś to dobrze. Prawdopodobnie nie będziesz zadowolony z poziomu oświetlenia, ponieważ błąd stanu ustalonego będzie zbyt duży. Będziesz musiał poprawić natężenie światła aby wygodnie czytać. Poprawki jakie wprowadziłeś, ostatecznie używając oczu, ilustrują ważną koncepcję. System sterowania w otwartej pętli może zostać ulepszony, jeśli powiemy jak dobrze jego dane wyjściowe odpowiadają wymaganiom danych wejściowych.
Sterownie W Zamkniętej Pętli
Systemy sterowania w pętli zamkniętej są również nazywane systemami sterowania ze sprzężeniem zwrotnym ponieważ informacje płyną wstecz w pewnym momencie w systemie sterowania. Zasadniczo ta odwrotna informacja przepływa z wyjścia systemu sterowania wstecz do wejścia. Informacje które płyną wstecz, umożliwiają systemowi sterującemu wprowadzanie poprawek w jego danych wyjściowych.
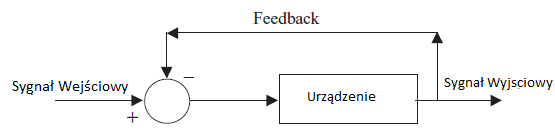
Zwrotny sygnał przepływu informacji nazwaliśmy "feedback" [sprzężenie zwrotne]. W tej prostej wersji układu sterowania z zamkniętą pętlą , sygnał wyjściowy jest wysyłany z powrotem i bezpośrednio porównywalny z wymaganiami ustawionymi przez sygnał wejściowy. Okrąg pokazuje obliczenia arytmetyczne (odejmowanie). Jeśli sygnał wyjściowy nie pasuje bezpośrednio do sygnały wejściowego, urządzenie otrzyma na wejściu sygnał niezerowy i dokona korekty na wyjściu aby jego wejście wróciło do zera. W praktyce istnieje wiele różnych rodzajów sterowania w pętli zamkniętej i jako takie mogą być różne warianty tego schematu. Wiele systemów sterowania nie ma danych wyjściowych które są bezpośrednio porównywalne z danymi wejściowymi; okrąg ze schematu musi być bardziej złożony niż w wypadku prostego odejmowania. Często sygnał wyjściowy musi zostać przekształcony zanim będzie można go porównać z sygnałem wejściowym. Takie przekształcenia mogą mieć postać skalowalną (do innego rozmiaru) lub konwersji z jednego rodzaju sygnału na inny (jak wartość światła na sygnał napięcia). Często porównanie wewnątrz okrągłego symbolu nie jest prostym odejmowaniem. Czasami jest to porównanie (większe lub mniejsze) a dane wyjściowe z okręgu przedstawiają albo włączenie albo wyłączenie. Na przykład termostaty działają w ten sposób. Oczywiście system wygląda jako zamknięta pętla. Często taki system jest również nazywany systemem sprzężenia zwrotnego w pętli zamkniętej. Wszystkie te terminy ogólnie oznaczają to samo. Zacznijmy pierwszy eksperyment ponownie w inny sposób, jako system sterowania w pętli zamkniętej. Teraz zamknij oczy i ponownie wskaż obiekt (próbując położyć palec na przedmiocie w polu widzenia). Otwórz oczy i zobacz jak blisko jesteś. Nadal nie udało ci się z zamkniętymi oczami ,ale teraz z otwartymi oczami, wprowadziłeś sprzężenie zwrotne do systemu. Z otwartymi oczami łatwo jest dokonać korekty i przesunąć palcem nad obiektem w polu widzenia. Zauważ ,że błąd stanu stabilnego jest teraz znacznie mniejszy. Uważamy, że błąd wynosi zero, ale wkrótce przekonasz się ,że tak zdarza się rzadko. Z pewnością,
kontrola w pętli zamkniętej jest lepszym rozwiązaniem pod względem dokładności, ale wiąże się z kosztem zapewnienia dodatkowych elementów kontrolnych (w tym przypadku, wizji)
Błąd Stanu Stabilnego
Teraz kiedy zidentyfikowaliśmy interesujący nas parametr, spójrzmy na to matematycznie. Możemy przypisać dowolne zmienne dla reprezentowania sygnałów i elementów sterujących, jak poniżej
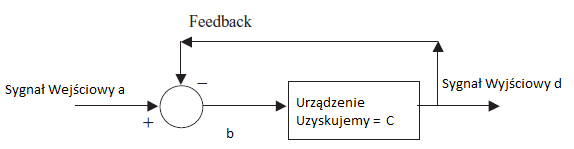
Patrząc na okrągły element arytmetyczny (odejmowanie) b = a - d
Urządzenie mówi, że uzyskało C. Wzmocnienie może być ogromne, ale system działa nadal. Przykładowo, jeśliw punkcie b mamy mały, dodatni sygnał b, wtedy sygnał d może być bardzo duży i dodatni. Podobnie, jeśli b, będzie małym, ujemnym sygnałem, wtedy d również będzie bardzo duże i ujemne. System został zaprojektowany do działania z sygnałem b, który jest bardzo mały, prawie zerowy. Urządzenie zazwyczaj zapewnia moc i wzmocnienie sygnału sterującego d. Precyzyjniej
d = C x b
Zastępując b z poprzedniego równania, otrzymujemy
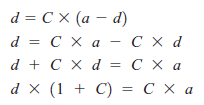
Na koniec uzyskujemy związek między sygnałem wejściowym a i sygnałem wyjściowym d :
d = a x *C/1 + C)
To równanie przewiduje ,że błąd stanu stabilnego tego rodzaju sterowania w systemie pętli zamkniętej jest regulowany przez C. Wyjście d będzie wyłączane przez współczynnik C/(1 + C). Współczynnik ten jest również określany jako współczynnik błędu stanu ustalonego. Zauważ, że nie może być zerem; błąd stanu ustalonego zawsze istnieje. Zwróć uwagę również ,ze im większe wzmocnienie C urządzenia, tym mniejszy błąd stanu stabilnego. Ponieważ C dąży do nieskończoności, błąd stanu stabilnego również dąży do zera. Jakie praktyczne rzeczy możemy wyciągnąć z takiej matematyki?
• Oczekujemy ,że system sterowania w pętli zamkniętej będzie wykazywał pewien błąd stanu stabilnego. Nie bądź zaskoczony jeśli system nie będzie wykazywał doskonałej wydajności. Z pewnością będzie miał błąd
• Rozpoznanie ,że błąd stanu stabilnego jest bardzo prawdopodobny i zależny od wzmocnienia urządzenia. Użyj współczynnika błędu stanu ustalonego aby oszacować z wyprzedzeniem, jaki błąd wystąpi i zaprojektować robota, aby umożliwił błąd w tym rozmiarze. Jeśli system ma zbyt duży błąd stanu stabilnego, należy rozważyć zmianę wzmocnienia urządzenia, w celu jego skorygowania
• Możemy sądzić ,że zwiększenie wzmocnienia urządzenia jak to tylko jest możliwe, jest pożądane. Należy jednak pamiętać ,że zwiększenie wzmocnienia urządzenia zwiększa koszty i wpłynie negatywnie na zachowanie dynamiczne (stan niestabilny) systemu sterowania , co zobaczysz później. W najgorszym wypadku duże wzmocnienie urządzenia może powodować niestabilność systemu i doprowadzić do awarii. Zmieniając wzmocnienie, pamiętaj o ponownym sprawdzeniu dynamicznych parametrów systemu sterowania
Uświadom sobie ,że te równania modelują ogólny system sterowania w pętli zamkniętej. Jeśli system sterowania ma kontrolować pozycję robota, wtedy zmienne a, b i d są miarą odległości. Jeśli ma kontrolować szybkość robota, zmienne te są miarą szybkości. Jeśli system ma kontrolować przyspieszenie robota, zmienne te są miarą przyspieszenia. Podstawy matematyki wciąż są takie same, zmieniają się tylko jednostki. Możemy użyć opisanych tu równań do kontrolowania dowolnego z wyżej wymienionych systemów bez dalszego badania. Pozostawimy czytelnikowi zbadanie matematykę rachunku różniczkowego, która utrzymuje ,że przyspieszenie jest pochodną prędkości, a prędkość jest pochodną pozycji. Wystarczy powiedzieć ,że dodatnie przyspieszenie zwiększa prędkość, ujemne przyspieszenie (hamowanie lub przyspieszenie w odwrotnym kierunku) zmniejsza prędkość, dodatnia prędkość gromadzi odległość (pozycję) a ujemną prędkość (ruch w tył) zmniejsza odległość (pozycje)
Reakcja Dynamiczna
Kiedy system sterowania widzi zmieniające się dane na wejściu, generalnie zmienia dane na wyjściu. Standardowy test systemu sterowania jest dostarczenie tak zwanego wejścia krokowego. W przypadku robota , takie wejście może oznaczać przejście z obecnej pozycji do nowej pozycji i zatrzymanie się. Klasyczne wejście używane do testowania systemu sterowania jest krokiem wejściowym i ma postać:
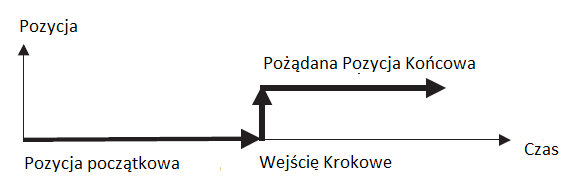
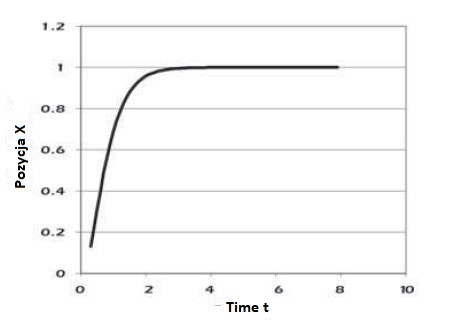
Idealny system sterowania będzie podążał za funkcją wejścia krokowego i stworzy taką samą funkcję wyjścia krokowego. Robot natychmiast przeniósłby się do nowej pozycji i zatrzymał precyzyjnie bez błędu stanu stabilnego. Wiemy jednak ,że robot będzie miał błąd stanu stabilnego (nie osiągając w pełni pożądanej pozycji końcowej). Prawda jest taka ,ze robot nie może natychmiast ruszać i zatrzymywać się precyzyjnie " w punkt". System sterowania w robocie widzi wejście krokowe ,opóźnia nieco czas reakcji, wreszcie zaczyna się poruszać i próbuje zatrzymać w pobliżu pozycji końcowej. Odpowiedź będzie niedoskonała. Zanim przyjrzymy się jak naprawdę zachowują się systemy sterowania, będziemy musieli się zatrzymać i zająć matematyką. Potem będziemy musieli użyć narzędzi aby zobaczyć co następuje:
• W jaki sposób projekt systemy sterowania określa sposób reakcji robota
• Jak scharakteryzować wydajność robota w kilku parametrach
• Jak sprawdzić , które parametry projektu zmienić w zależności od wydajności robota
• Jak uzyskać optymalną wydajność robota
Aby uzyskać narzędzia potrzebne do analizowania i manipulowania wydajnością robota, wybieramy model matematyczny dla robota i wyprowadzamy pewne równania. Pominiemy łatwiejsze modele zachowania robotów i przejdziemy do nieco bardziej złożonego przypadku. Zamierzamy użyć matematyki i fizyki, które mogą wykraczać poza zwykłe umiejętności czytelnika, ale powrócimy do użytecznego, intuicyjnego modelu tego co się dzieje. Zaczniemy od fizyki, rachunku różniczkowego, transformaty Laplace′a i algebry dla uzyskania przydatnych wyników. Kiedy będziemy już mieli tą matematykę przed sobą, zbadamy narzędzia które nam do dało. Po pierwsze , potrzebujemy sposobu aby spojrzeć na części robota i przypisać liczby do ruchów , które obserwujemy. Można to zrobić na kilka sposobów:
• Oszacowanie energii. Jednym ze sposobów analizy dynamicznego ruchu jest spojrzenie na wszystko pod kątem energii : gdzie jest przechowywana i jak jest używana. Nie będziemy używać tej techniki ,ale warto wspomnieć o alternatywnej technice. Energia jest przechowywana w wielu miejscach w robocie, na pewno w akumulatorach, ale również czasów jest przechowywana w innych miejscach
• Sprężyny (energia potencjalna). Dobry opis matematyczny sprężyny podamy później. Gdy sprężyna jest ściśnięta, energia E w sprężynie wynosi:
E = 0,5 x K x x2.
gdzie x jest dystansem ściskania. Zwróć uwagę ,że to równanie działa tylko dla mniejszych wartości x , ponieważ nadmiernie ściśnięta sprężyna staje się nieliniowa i kończy się sprężystość. K jest stałą sprężystości , większa, mocniejsza sprężyna ma większą wartość K.
• Masa ruchoma (energia kinetyczna) .Energia w poruszającej się masie
E = 0,5 x m x 2,
gdzie m to masa, którą opiszemy później, v to prędkość. Zwróć uwagę ,że ruchoma masa może poruszać się nie tylko liniowo. Może również się obracać. Jeśli tak, możesz modelować energię obu ruchów oddzielnie. Możesz użyć środka ciężkości masy i zobaczyć jak szybko porusza się liniowo. Następnie możesz dodać energie obrotu wokół tego środka masy (jeśli ją odkryjesz)
" • Masa na wysokości (energia potencjalna) .Gdy masa znajduje się na wysokości, jej energia potencjalna jest określona równaniem
E = m x g x h
gdzie M to masa, g to stałe przyspieszenie ziemskie 9.8 m/s2, , h to wysokość z jakie masa może spaść.
• Oszacowanie siły. Zamiast patrzeć na energię użyjemy techniki patrzenia na wszystko w kategoriach siły. Musimy tylko scharakteryzować siły w systemie, ponieważ działają razem. W ten sposób możemy przewidzieć co zrobi fragment robota. A oto kilka miejsc przechowywania siły w robocie:
- Siły Silnika. Większość silników generuje zmienną w czasie siłę przy stosowaniu energii. Siła może być obrotowa lub liniowa. Aby zachować prostotę, będziemy przyglądać się sile liniowej, takiej jaką może przenosić solenoid. który jest elektromagnesem z ruchomym rdzeniem metalowym.
- Siła masy ruchomej (energia kinetyczna). Newton stworzył równanie dla siły działającej na masę ( lub masę wytwarzającą siłę):
F = m x A
gdzie m jest masą a A jest przyspieszeniem (lub opóźnieniem). Kiedy siła grawitacji jest siłą zapewniającą przyspieszenie , A = g a zatem F = m x g , siła potrzebna dla utrzymania masy m
• Siła sprężyny. Sprężyna ze stałą sprężystości K będzie miała siłę, w której z jest ściskaniem (lub wydłużeniem) sprężyny
• Siła tarcia. Tarcie jest siłą która jest wywoływana przez prędkość poprzez środek tarcia. Na przykład, silnik, kiedy wyłączone zostanie zasilanie, spowoduje zatrzymanie silnika siłą rozpędu ponieważ jego wirnik ślizga się po łożyskach, a smar w łożyskach nadal ma tarcie. Spadek prędkości jest nieco liniowy w czasie. Tarcie jest proporcjonalne do prędkości i ma siłę
F = B x v
gdzie B jest współczynnikiem tarcia, a v to prędkość. Czyni to intuicyjnym sens. Kiedy pocierasz ręce, musisz pracować ciężej by pocierać szybciej. Tarcie staje się gorętsze im szybciej pocierasz. Siła wzrasta a energia rośnie szybciej. Tarcie przychodzi do nas w przebraniu. Często myślimy o tarciu jako o czymś co ciągniemy po powierzchni. Często, elementy będą miały własne tarcie wewnętrzne. Silnik sam się zatrzyma. Sprężyny nagrzewają się przy odbijaniu, i powoli przestają się odbijać. Jeśli współczynnik tarcia nie jest określony wewnątrz systemu, możemy go często określić empirycznie. Szybkim sposobem zrobienia tego jest obliczenie chwilowego opóźnienia masy i porównanie dwóch sił:
F = m x dla masy
F = B x v dla tarcia, więc
B = m x a/v
Ta technika działa dla ruchów obrotowych, liniowych i sprężystych
Teraz musimy wybrać mechaniczny model robota, aby stworzyć dla niego model matematyczny. Wybieramy dowolny model, który prawdopodobnie różni się od rzeczywistej mechaniki naszego robota. Jednak, kiedy nauczymy się analizować i manipulować tymi arbitralnym modelem, będzie to naszą drugą naturą aby poszerzać wiedzę na inne modele. Większość systemów, nawet nietypowych, nieliniowych z ruchami nieregularnymi, może być traktowana podobnie do modelu, który będziemy badać. Matematyka jest bliska tego samego. Spójrzmy na tzw. system drugiego rzędu, ponieważ siły są oparte na trzech różnych reprezentacjach pozycji (przedstawionych w kategoriach rachunku różniczkowego) :
• Pozycja. Pozycja x ,masy. W przypadku sprężyn, siła jest proporcjonalna do x
• Prędkość. v, szybkość zmiany położenia x, masy , pierwsza pochodna z x. W rachunku różniczkowym nazywa się to pierwszą pochodną z x względem czasu (v = dx/dt). W codziennym życiu myślimy o tym jako kilometrach na godzinę. Siła tarcia jest proporcjonalna do dx/dt
• Przyspieszenie. a jest szybkością zmiany prędkości, pierwsza pochodna z v, druga pochodna pozycji x. W rachunku różniczkowym a = dv/dt, lub kiedy piszemy z wyrazem x, a = d2x / dt2
W prostym systemie, w którym przysp
ieszenie jest stałe (np. grawitacja działająca na spadający obiekt blisko powierzchni ziemi):
v = a x t
x = 0,5 x a x t2.
Najprostszym mechanicznym modelem drugiego rzędu jest ciężar zawieszony na sprężynie. Zastanówmy się hak zachowuje się ten system. Zamierzamy przestawić schematy zachować, po jednym na raz i wyliczyć zachowania abyśmy mogli później to wyjaśni gdy mamy już równania
1. Po przesunięciu ciężaru (masy) w pionie i zwolnieniu go, będzie odbijał w górę i w dół przy stałej częstotliwości. Jeśli przemieszczenie utrzymuje sprężynę w jej obszarze liniowym (bez jej ściskania lub rozciągania zbyt mocno), ruch masy będzie podobny do fali sinusoidalnej
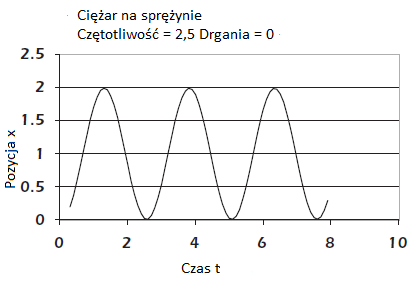
Ilustruje to częstotliwość rezonansową systemu drugiego rzędu, którą później nazwiemy v. Częstotliwość v jest mierzona w radianach na sekundę, gdzie mammy 2 x π radianów w pojedynczym cyklu
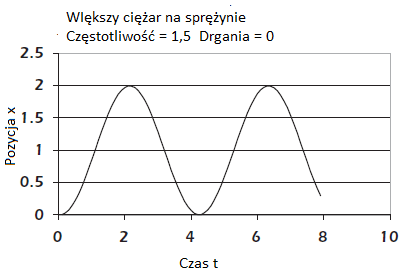
2. Wiemy, że jeśli obciążymy sprężynę, ciężar będzie odbijał w górę i w dół niż robi to lżejszy ciężar. Aby to wypróbować, zawieś dwa ciężarki na gumce. To ilustruje w jaki sposób ? maleje wraz z masą
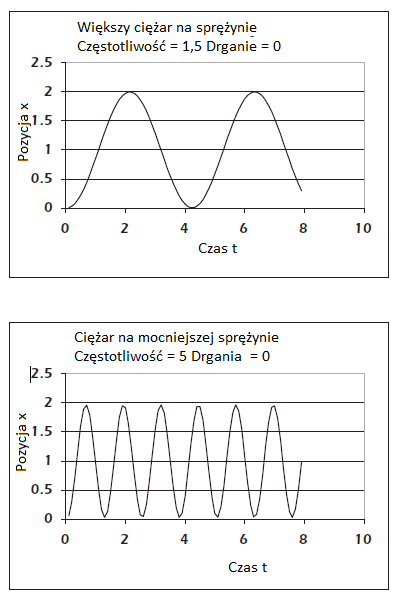
3. Wiemy, że mocniejsza sprężyna sprawia ,że ciężar będzie szybciej odbijał się w górę i w dół niż słabsza sprężyna. Aby to sprawdzić, drugą gumkę, tuż obok pierwszej tak aby działały zgodnie
i użyj oryginalnego ciężaru pojedynczego. Ilustruje to w jaki sposób ? rośnie ze stałą sprężystości K
4. Wiemy, że podskakujący ciężar ostatecznie się uspokoi i przestanie podskakiwać jeśli przestaniemy przesuwać sprężynę. Ilustruje to tłumiące działanie tarcia. W tym szczególnym przypadku tarcie znajduje się wewnątrz samej sprężyny (i w powietrzu). Gumki nagrzewają się gdy tarcie wewnątrz gumki zużywa energię, która była w ruchu ciężarku. Później pomówimy o współczynniku tłumienia ?. Oczywiście, jeśli spróbujemy tego pod wodą, zamiast w powietrzu, tarcie będzie znacznie większe, a system osiądzie dużo szybciej
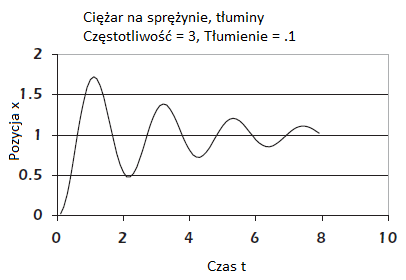
5. Wiemy ,że w miarę przesuwania górnej części gumki w górę (tak jak pokazane wcześniej wejście krokowe), ciężar będzie wystrzeliwał wyżej niż pożądana pozycja końcowa i ostatecznie osiada na wyższym poziomie. Nazywamy to nadmiernym ruchem ciężaru przeregulowania
Teraz czas na diagram naszego modelu systemu mechanicznego. Zamiast wiszącego ciężaru, wyeliminujemy siłę grawitacji i użyjemy systemu poziomego , gdzie ciężar spoczywa na śliskiej powierzchni. Jeśli chcesz wziąć ten układ poziomy i ekstrapolować do układu pionowego, po prostu rozciągnij sprężynę aby przeciwdziałać przyspieszeniu siły grawitacji na masę. Dla naszych obliczeń, model poziomy pobiera te wyrażenia z matematyki, ponieważ grawitacja nie rozciąga sprężyny
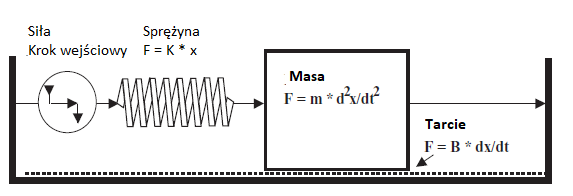
Podstawą odniesienia jest w tym przypadku ziemia. Nie powinna ona się ruszać pod Tobą. W rzeczywistości, kiedy idziesz w jedną stronę, ziemia obraca się w przeciwną stronę. Ale ponieważ jest o wiele większa od Ciebie, ruch jest niedostrzegalny. Pozostawiam to Tobie, aby obliczyć rotację Ziemi, która miałaby miejsce gdyby wszyscy na Ziemi zaczęli iść w tym samym kierunku. Na razie załóżmy że grunt jest stabilny. Zagłębimy się w fizykę i matematykę bez poważnej próby wyjaśnienia jak to działa. Siła w zamkniętej pętli elementów mechanicznych sumuje się do zera. Na podstawie tego otrzymujemy "charakterystyczne" równanie różniczkowe tego systemu mechanicznego:
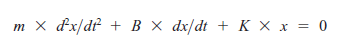
To mówi, że siła sprężyny działa , próbując przyspieszyć masę i pokonać tarcie. W rachunku różniczkowym, istnieje wiele sposobów rozwiązania takiego równania różniczkowego jak ten. Matematyka jest trochę trudna, ale francuski matematyk Laplace zapewnił skrót w postaci transformaty Laplace'a. Zasadniczo eliminuje ona wymagania rachunku całkowego i redukuje problem di algebry i przeszukiwania pewnych tablic. Dokonamy transformacji Laplace'a na nasze równanie różniczkowe, wykonamy algebrę, a następnie wykorzystamy tabele do przeprowadzenia transformacji odwróconej Laplace'a aby odzyskać naszą odpowiedź w świecie rzeczywistym. Najpierw przekształcimy nasze równanie różniczkowe za pomocą metod Laplace'a. Zastępujemy zmienną s oznaczającą pojedyncze różniczkowanie. Jedno takie równanie różniczkowe staje się :
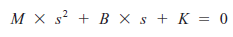
Zamierzamy użyć algebry aby znaleźć pierwiastki równania kwadratowego. Pamiętasz stary wzór dla znajdowania pierwiastków równania kwadratowego? Założę się ,że nie myślałeś, że będziesz go używał! Poniżej ponownie mamy równanie kwadratowe i jego dwa pierwiastki. Zauważ ,że te dwa pierwiastki są pokazane ze znakiem + i - :
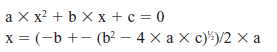
Zamierzamy użyć równania kwadratowego do rozwiązania naszego równania charakterystycznego. Po pierwsze, trochę pooszukujemy, ponieważ już znamy odpowiedź. Zamierzamy zmienić niektóre stałe w równaniu charakterystycznym przed rozwiązaniem dla pierwiastków. Pozwoli to nam łatwo zauważyć wynik końcowy. Oto trzy zmiany jakie wprowadzimy:
- Dzielimy przez K więc
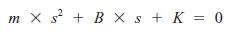
zmienia się w
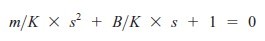
-Zastępujemy 1/ω2dla m/K. Przyjrzyj się drugiemu i trzeciemu zachowaniu podskakującego ciężaru a docenisz tą zmianę
-Zastępujemy 2 x δ/ω dla B/K. Współczynnik tłumienia δ, stanowiący integralny element spowalniający system w czasie, jest bezpośrednio związany ze współczynnikiem tarcia, jak można się było spodziewać. Równanie zmienia się wraz z podstawieniem z
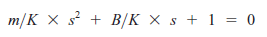
na
Używając równania kwadratowego, mamy dwa pierwiastki
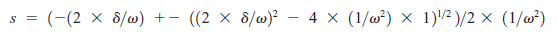
Wyciągamy współczynniki 2 :
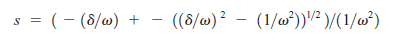
Pomnożenie góry i dołu przez ω2 przenosi nas do dwóch pierwiastków kwadratowego:
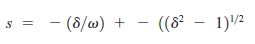
Teraz dokonamy odwrotnej transformaty Laplace'a używając tabel (które nie są replikowane). W przypadku gdy d jest mniejsze niż 1, mamy tzw. system bezwarunkowy , który reaguje bardzo podobnie jak wykres przeregulowania. W tym przypadku tabele Laplace'a pokazują podstawowe rozwiązanie
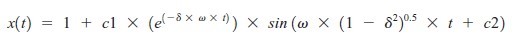
gdzie c1 i c2 mają być określone przez warunki początkowe. Aby znaleźć warunki początkowe, przyjrzymy się równaniom dla reszty stanów x i dx/dt. Daje nam to dwa równania z dwoma niewiadomymi i prowadzi to równania końcowego :
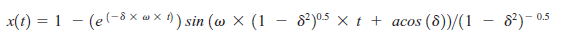
Jest to ostateczne rozwiązanie i zostanie użyte do wcześniejszego wygenerowania wykresów. To równanie reprezentuje funkcję kroku jednostkowego począwszy od x = 0 w czasie 0 i ustalenie wartości x = 1 po ustabilizowaniu się stanów nieustalonych. Widać to w zachowaniu poszczególnych funkcji w rozwiązaniu. Funkcja wykładnicza e(-? x ? x t) zanika z czasem t i dąży do nieskończoności. Im większe tłumienie, tym szybciej. Funkcja oscyluje i zapewnia dzwonienie
Projektowanie Systemy Sterowania
Cóż, przeszliśmy przez matematykę i wymyśliliśmy zamknięte rozwiązanie w jaki sposób zachowuje się system modelowy. Jak możemy to wykorzystać? Pamiętaj o naszych celach: zamierzmy odpowiedzieć na poniższe pytania:
• W jaki sposób projekt systemu sterowania określa sposób reakcji robota
• Jak scharakteryzować wydajność robota i jakie parametry projektu zmienić
• Jak zmienić parametry konstrukcyjne robota
• Jak uzyskać optymalną wydajność z robota
Zajmijmy się naszym pierwszym celem
W jaki sposób projekt systemu sterowania określa sposób reakcji robota?
Zrobiliśmy model sytemu drugiego rzędu i mamy zamknięte równania opisujące zachowanie modelu. Jeśli znamy m , K i B, możemy wykreślić teoretyczne zachowanie systemu. Oto krok po kroku jak to zrobić:
1. Jeśli masz wartości m, K i B , przejdź do kroku 2
a. Masa. Aby zmierzyć masę m, po prostu zważ ją w kilogramach i podziel przez przyspieszenie grawitacyjne 9,8 m/sec2. Należy tu wspomnieć ,że kilogram nie jest miarą wagi. Rzeczywistą jednostką masy w systemie metrycznym jest Newton. Nie jest poprawne zgłaszanie wagi w kilogramach. Powinieneś być świadom ,że masa to nie to samo co waga. Masa jest miarą ilości "rzeczy" w obiekcie. Waga jest siłą i jest miarą siły wywieranej przez masę w obecności grawitacji stworzonej przez inną masę, taką jak Ziemia. Masa na orbicie jest nieważka, ale zachowuje swoją masę. Masa na Ziemi staje się ciężarem ponieważ działa na nią przyspieszenie grawitacyjne (F = m x g). To podnosi ważną kwestię. Obliczenia dla modelu systemu drugiego rzędu są częściowo zależne od siły grawitacji. Robot może nie działać tak samo na orbicie. Tarcie, które wykreśliliśmy w mechanicznym modelu systemu drugiego rzędu, zależy od tarcia masy spoczywającej na powierzchni. Bez grawitacji nie będzie mowy o takim współczynniku tarcia B. Możesz wprowadzić inne elementy tarcia do projektu swojego robota, które działają na orbicie, takie jak tłok z lepkim płynem wewnątrz niego (jak amortyzator)
b. Stała sprężystości. Aby zmierzyć stałą sprężystości K, zawieś znaną masę na sprężynie bez jej rozciągania zbyt daleko. Stosunek przemieszczenia sprężyny do ciężaru da Ci K, używając wzoru
m x g = K x przemieszczenie
gdzie g = 9,8 m/sec2, przyspieszenie grawitacyjne. Przykładowo mamy ciężar 250 gramów zawieszony na sprężynie
m x g = K x przemieszczenie
250 gram 9,8 m/sec2 = K x przemieszczenie
K = (2,4 kgm/ sec2
Zawieś 250 gramowy ciężar , zmierz przemieszczenie w metrach, a potem wylicz K w newtonach na metr.
c. Współczynnik tarcia
i. Po pierwsze, musisz wiedzieć jak zachowuje się tarcie, ponieważ może stać się skomplikowane. Tarcie jest większe w naszym modelu, gdy ciężar się nie porusza. Jest to określane jako tarcie statyczne. Gdy masa zaczyna się poruszać, tarcie spada do niższego poziomu, tak długo jak długo masa się porusza.
Pomyśl o tarciu jako o serii mikroskopijnych progów zwalniających. Nie wydają się być nierówne, jeśli ciężar porusza się szybciej, ale jeśli ciężar zwalnia do pełzania , progi zwalniające są bolesne do przejścia. Wszyscy wcześniej doświadczaliśmy tarcia statycznego
ii. Współczynnik tarcia B może być zmierzona na dwa sposoby:
Konwersja siły: weź sprężynę ze znaną stałą sprężystości K i użyj jej do ciągnięcia ciężaru ze stałą prędkością dx/dt przez powierzchnie cierną. Siła wywierana przez sprężynę to K x x , gdzie x jest przemieszczeniem sprężyny. Przy stałej prędkości, siła sprężyny jest równa sile tarcia, którą jest B x dx/dt
B = K x x/(dx/dt)
Wyprowadzenie: Zobaczymy później jak , znając K i m , możemy wyprowadzić B, obserwując zachowanie systemu. Byłoby to użyteczne, gdy trzeba zmienić jeden z trzech parametrów, aby zmienić zachowanie systemu.
2. Załóżmy ,że znamy B , K i m. Możemy podłączyć te liczby do równania dla x(t) i wykreślić przewidywane wyniki. Robot powinien podążać za zachowaniem modelu jeśli model rzeczywiście naśladuje projekt robota.
Zajmijmy się drugim celem
Jak scharakteryzować wydajność robota i jakie parametry projektu zmienić
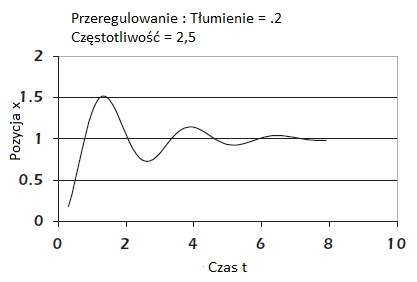
Poniższe rysunki pokazują przewidywane zachowanie modelu systemu drugiego rzędu. Zostały one stworzone specjalnie po to aby pokazać jak można kierować projektem i sprawić by robot zachowywał się tak jak chcemy. To oczywiście nasz trzeci cel, więc odłożymy na razie te dywagacje. Każda pojedyncza krzywa na rysunkach przedstawia przewidywane zachowanie układu sterowania drugiego rzędu, z uwzględnieniem określonych parametrów projektu, na które B, K i m. Każda krzywa na rysunkach jest znormalizowana i pokazuje układ sterowania, który ostatecznie ustali na wartość 1. Ze względu na różnice (odzwierciedlone w każdej krzywej), zachowują się one inaczej. Kluczem jest dla nas poznanie, jak zachowują się te krzywe i jak je kontrolować. Pierwszą rzeczą , którą należy zauważyć na temat tych dwóch liczb, jest przewidywalność krzywych. Na rysunku, oznaczonym Tylko Różne Tłumienia, widać ,że wszystkie krzywe mają mniej więcej tę samą częstotliwość
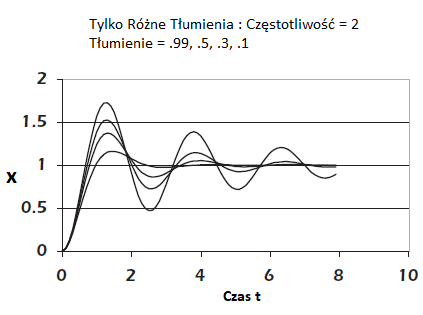
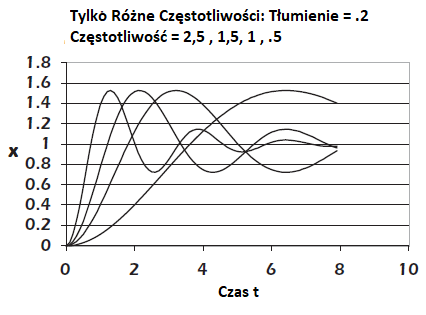
Środkowa linia pozioma reprezentuje końcową wartość 1. Wszystkie krzywe przecinają linię środkową mniej więcej w tym samym czasie : 2,5 sekundy, 4 sekundy , 6 sekund. Wynika to z tego ,że każdy z systemów drugiego rzędu został zaprojektowany tak ,aby miały tę samą częstotliwość. Krzywe te pokazują wpływ zmiany tłumienia. Na rysunku oznaczonym Tyko Różne Częstotliwości, widzimy ,ze krzywe mają mniej więcej takie samo przekroczenie i spadek. Wszystkie osiągają wartość 1,5, spadają do wartości 0,75 itd. Wynika to z faktu, że każdy z tych systemów drugiego rzędu został zaprojektowany tak, aby miał takie samo tłumienie. Krzywe te pokazują wpływ zmiany częstotliwości. Przeanalizujemy charakterystykę krzywych na wykresie i przedyskutujemy, które cechy są bezpośrednio interesujące.
Projektanci robota rozważają następujące rzeczy:
• Czas reakcji. Spójrz na rysunek nazwany "Tylko Różne Częstotliwości". Utrzymuje parametr tłumienia δ stałym a zmienia się częstotliwość ω. Chodzi o to ,że krzywe rosną w kierunku wartości końcowej 1 przy różnych prędkościach. Dostępnych jest kilka sposobów pomiaru czasu reakcji, w tym
- Czas od 0 do pierwszego przekroczenia 1
- Czas od 0 do pierwszego przekroczenia wartości szczytowej (wartość maksymalna)
System ma inny czas reakcji dla różnych wartości tłumienia. Jeśli spojrzymy na czas od 0 do pierwszego przekroczenia, cztery krzywe różnią się narastania od 3/4 sekundy do 4 sekund. Te cztery krzywe zmieniają się w zakresie od 2,5 do 0,5 radianów na sekundę. Okrąg ma 2π radianów. Częstotliwość jest związana z radianami w następujący sposób :
F = 2 x π x ω
gdzie F jest w hercach (cykli na sekundę), ω jest w radianach na sekundę, a π to 3,14159… Biorąc pod uwagę, że cykl zawiera 2 x π radianów, cztery krzywe reprezentują częstotliwości od 0,4 do 0,08 Hz i okres (1/częstotliwość) od 2,5 sekundy do 12,5 sekundy. Spójrzmy na tabelę niektórych z tych wartości i zobaczmy jak odnoszą się one do czasu odpowiedzi
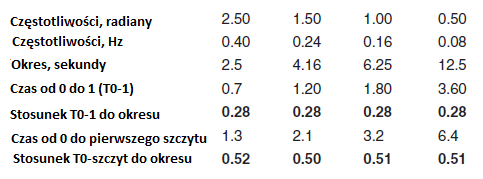
Oto dwie praktyczne zasady. Liczby te pomagają upewnić się ,że system reaguje wystarczająco szybko, aby spełnić Twoje wymagania:
- Czas odpowiedzi od t = 0 do krzywej osiągającej wartość 1 wynosi około 28 procent tego okresu. Okres może być wyliczony z ? jak uszczegółowiono powyżej. Pozwala Ci to wybrać czas narastania, gdy wybierzesz ω
- Czas odpowiedzi pd t = 0 do pierwszego szczytu wynosi około 51 procent okresu (jak można się spodziewać po fali sinusoidalnej)
• Przekroczenie. Spójrz na rysunek nazwany Tylko Różne Tłumienia. Stworzony został przy stałej częstotliwości ω i zmienną stałą tłumienia δ. Krzywe przekraczające pożądany poziom o różne wartości. Im mniejsze tłumienie, tym większe przeregulowanie. Przekroczenie może być ważne , ponieważ może spowodować utratę kontroli nad finalnym celem.
• Czas regulacji. Możesz myśleć ,że zwiększanie tłumienia jest zawsze pożądane w celu zmniejszenie "dzwonienia" i przyspieszenia systemu. Z pewnością wraz ze wzrostem tłumienia system wygląda mniej szaleńczo i zbiega się do wartości końcowej 1. Zwiększając tłumienie, czas reakcji również wzrasta , więc będziesz musiał dokonać kompromisu dopasowanego do projektu robota. Tłumienie dotyczy jedynego parametru, który można zwiększyć, co poprawi czas reakcji.
• Częstotliwość oscylacji. Czasami system sterowania będzie jeszcze bardziej skomplikowany niż system drugiego rzędu. Czasami mechanika lub elektronika są wrażliwe na określone częstotliwości oscylacji. Może się to zdarzyć, jeśli masa w modelu ma częstotliwość mechaniczną rezonansu. Pamiętasz most Galloping Gerdie? Rozpadł się na kawałki , ponieważ inżynierowie mechanicy nie zauważyli tłumienia rezonansowej częstotliwości mechanicznej. Mówimy o braku o kontroli tłumienia.
• Więcej zmiennych. Przez cały czas zakładaliśmy ,że zarówna masa jak i tarcie poniżej masy są ustalane w odniesieniu do częstotliwości, gdy zmienia się pozycja masy. Jeżeli masa nie jest masywna, ale ma rezonans harmoniczny w swojej strukturze, wówczas system nie będzie się zachowywał per model Bądź więc bardzo ostrożny, aby twój robot miał solidną konstrukcję i jak najmniej rezonujących elementów mechanicznych. O wiele łatwiej jest kontrolować pozycję jednokilogramowego bloku stali niż kontrolowanie jednokilogramowej miski galaretki . Jeśli współczynnik tarcia zmienia się w zależności od pozycji, mogą wystąpić podobne problemy. Musimy jasno zidentyfikować wszystkie elementy tarcia działające w naszym systemie robota. Niektóre będą nieodłączne od materiałów (jak w sprężynach). Inne elementy tarcia będą przypadkowe i muszą zostać starannie przenalizowane ,aby upewnić się
,że pozostanie na stałym poziomie. Nie jest rozsądne pozwolić nieokreślonym elementom
ciernym rozregulować nasz system. Aby przejąć kontrolę nad projektem, możemy celowi wprowadzić do naszego systemu element cierny z własnego wyboru.
• Stabilność. Cała teoria systemów sterowania jest poświęcona stabilności systemu. Z przykładu mostu wiemy, że jest to ważne. Jest to również bardzo skomplikowane w teorii matematycznej i nie powinniśmy w to wchodzić, ale powinniśmy przyjrzeć się kilku radom. Po pierwsze powinniśmy określić jaka jest niestabilność. Niektóre systemy sterowania , jeśli nie są zaprojektowane poprawnie, mogą zbytnio oscylować, zaburzyć mechanikę i zrujnować działanie robota. Te oscylacje mogą wynikać z różnych wad w projekcie.
* Częstotliwości rezonansowe. Jak już wspomnieliśmy, upewnij się ,ze mechanizmy i inne elementy fizyczne układu, takie jak elementy cierne i elementy sprężyste, nie mają częstotliwości rezonansowych. Upewnij się ,że zachowują się w ten sam sposób we wszystkich częstotliwościach, którym zostanie poddany robot.
* Zły dobór częstotliwości ω. Czasami system mechaniczny ma pewne częstotliwości rezonansowe. Jeśli ? zostanie źle wybrana dzwonienie może być zbyt duże a system może być niestabilny. Zmień ω i sprawdź czy wszystko się uspokoi. Jeśli to pomoże, ponownie przeanalizuj mechanikę.
* Elementy nieliniowe. Musimy zdać sobie sprawę ,że nasz model zależy od zachowania liniowego wszystkich tych komponentów. Oczekujemy płynnego działania dookoła . Między luźnymi kawałkami (które mogą się swobodnie poruszać a następnie mocno napiąć) a niektórymi "cyfrowymi" elementami (które są wyłączone), nastąpi gwałtowny ruch
* Zbyt duże przeregulowanie. Czasami system przesuwa robota za daleko i nie może go odzyskać. Taka sytuacja miał miejsce we wstępie, gdzie robot przesunął się za daleko w jednym ruchu , a jego ograniczone "oku" nie dano czasu aby zobaczył ,że przekroczył granicę , na której miał się zatrzymać. Taka sytuacja może wystąpić , jeśli przekroczymy zbyt duo. Jedynym rozwiązaniem jest zwiększenie tłumienia w systemie
* Złożone projekty. Często robot jest znacznie bardziej skomplikowany niż system drugiego rzędu. Jeśli naprawdę jest to system trzeciego lub wyższego rzędu, poświęć trochę czasu aby o uprościć. Spójrz na wydajność i sprawdź specyfikacje. Załóżmy ,że próbujemy zaprojektować robota bejsbolowego. Musi moc biec, łapać i rzucać. Może być w stanie biec i łapać w jednej chwili, ale byłoby prościej zbudować robota, który biegłby pod piłkę, zatrzymał się, a następnie ją złapać. Podobnie byłoby prościej, gdyby robot przestałby biec, zanim musiałby rzucić piłkę. To prawda ,że człowiek grający w baseball nigdy nie dostałby się do głównej ligi grając w ten sposób. Jednakże, jeśli specyfikacje i wymagania dotyczące wydajności mogą zostać złagodzone z wyprzedzeniem i jeśli możemy pozwolić sobie na niezgrabnego robota - gracza, wtedy nasz projekt będzie dużo prostszy jeśli możemy podzielić projekt. Następnie oddzielnie projektujemy biegacza, łapacza i rzucającego. Nie musimy łączyć projektów i cierpieć z powodu interakcji, które podnoszą złożoność i zagrażają stabilności naszego projektu. Ponownie ponawiamy starą zasadę : Zachowaj prostotę
Jak więc ustabilizować system? Może wystąpić kilka objawów. Łatwo je zaobserwować i poprawić:
• Poważne przeregulowanie. Czasami przekroczenie może stać się bardzo duże. Możemy to naprawić , zwiększając stałą tłumienia δ. Zmiana ? nie wpływa zbytnio na przeregulowanie. Jeśli zmiana nie pomoże, być może robot nie podążą za modelem i powinniśmy ustalić dlaczego
• Silne dzwonienie (drgania powodujące problemy). Aby to naprawić, możemy zwiększyć stałą tłumienia δ. Pomoże to w szybszym zmniejszeniu oscylacji. Jeśli oscylacje nadal budzą
zastrzeżenia, musimy zbadać, dlaczego jest to sytuacja w której robot jest podatny na drgania o określonych częstotliwościach, rozważ zmianę częstotliwości na taką która może lepiej działać w systemie.
• Nieznane oscylacje. Czasami roboty nie podążają za modelem i zachowują się właściwie. W porządku . Dzieci zachowują się tak sam, a to wszystko jest częścią radości życia. Powoduje to ,że niestabilności mogą się rozwijać z silnymi wibracjami lub nawet dzikim zachowaniem. Z dziećmi można poeksperymentować , przez ograniczenie cukru. W przypadku robotów możemy rozważać podjęcie dwóch działań:
- Wykonaj wymienione wcześniej czynności ,aby pozbyć się silnego dzwonienia
- Poszukaj błędów konstrukcyjnych w mechanice i systemie sterowania, które sprawiają ,że będzie bardziej skomplikowany niż system drugiego-rzędu, który próbujemy. Poszukaj miejsc w których energia może być przechowywana , a czego się nie spodziewaliśmy. Zmień projekt, aby to zrekompensować
Co się stanie, gdy weźmiemy system drugiego rzędu i spróbujemy go umieścić w systemie pętli zamkniętej ze sprzężeniem zwrotnym? Cóż, rozważmy następujący system sterowania pętli zamkniętej ze sprzężeniem zwrotnym
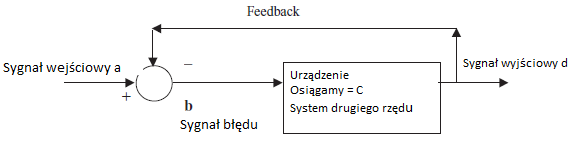
Załóżmy ,że urządzenie jest układem drugiego rzędu, taki jak ten który badaliśmy. Jak widzieliśmy, nie zareaguje natychmiast na funkcję wejścia krokowego. Przechodzi przez pewne opóźnienie, czas narastania, a następnie czas regulacji. Załóżmy ,że dziko wprowadziliśmy dane wejściowe do sygnału wejściowego. Ponieważ urządzenie nie zareaguje od razu, sygnał wyjściowy d nie zmienia się od razu. Sygnał błędu b będzie odzwierciedlał nasze dzikie dane wejściowe. Sygnał wejściowy urządzenia może również zawierać bardzo zmienne dane wejściowe. Sygnał wejściowy urządzenia może również zawierać bardzo zmienne dane wejściowe. Jeśli nasze sygnały wejściowe fluktuowały gdzieś w pobliżu częstotliwości naturalnej ?, systemu, sygnał wyjściowy może rzeczywiście nie być w fazie z sygnałem wejściowym. Dokładnie tak się dzieje, gdy mamy nadsterowny samochód. Zawieszenie samochodu można modelować jako system drugiego rzędu, w którym:
- Masa jest reprezentowana przez sam samochód
- Sprężyny znajdują się w zawieszeniu
- Tarcie tłumiące znajduje się w amortyzatorach
Załóżmy ,że urządzenie jest układem drugiego rzędu, taki jak ten który badaliśmy. Jak widzieliśmy, nie zareaguje natychmiast na funkcję wejścia krokowego. Przechodzi przez pewne opóźnienie, czas narastania, a następnie czas regulacji. Załóżmy ,że dziko wprowadziliśmy dane wejściowe do sygnału wejściowego. Ponieważ urządzenie nie zareaguje od razu, sygnał wyjściowy d nie zmienia się od razu. Sygnał błędu b będzie odzwierciedlał nasze dzikie dane wejściowe. Sygnał wejściowy urządzenia może również zawierać bardzo zmienne dane wejściowe. Sygnał wejściowy urządzenia może również zawierać bardzo zmienne dane wejściowe. Jeśli nasze sygnały wejściowe fluktuowały gdzieś w pobliżu częstotliwości naturalnej ?, systemu, sygnał wyjściowy może rzeczywiście nie być w fazie z sygnałem wejściowym. Dokładnie tak się dzieje, gdy mamy nadsterowny samochód. Zawieszenie samochodu można modelować jako system drugiego rzędu, w którym:
- Masa jest reprezentowana przez sam samochód
- Sprężyny znajdują się w zawieszeniu
- Tarcie tłumiące znajduje się w amortyzatorach
Jak zmienić parametry konstrukcyjne robota
Widzieliśmy już ,że zmiana ω i δ mogą znacząco zmienić wydajność robota. Ponadto zmiana tych parametrów oferuje niezawodny sposób na zmianę tylko jednego rodzaju zachowania naraz, bez znacznego zakłócania innych zachowań. Na przykład, zmiana δ powoduje tylko przeregulowanie z minimalnymi zmianami czasu narastania. Zmiana ? zmienia tylko częstotliwość dzwonienia przy minimalnych zmianach przekroczenia. Oto jak zmienićω i δ:
• Zmiana ω
- Wiemy, że 1/&omea2 = m/K
- ω = (K/m)0,5 ,
- Zmieniamy ω, zmieniamy K lub m lub oba. Możemy zmienić K przez włożenie innej sprężyny/ Sztywniejsza sprężyna ma wyższą wartość K. Możemy zmienić m zmieniając masę robota.
- Strzeż się!
* Wiemy ,że 2 x δ/ω = B/K
* Jeśli zmienimy ω lub K, wtedy musimy zmienić B jeśli chcemy zachować stałe δ
• Zmiana δ
- Wiemy ,że 2 x δ/ω = B/K
- Biorąc pod uwagę ,że ? jest stałe, aby zmienić ?, zmień B jeśli to możliwe. Zmień tylko K jeśli musisz
- Strzeż się!
* Wiemy ,ze 1/ω2 = m/K
* Jeśli zmienimy K, wtedy zmienimy m dla utrzymania stałego ω
- Większość z nas zna konkretny sposób zmieniania δ Wiele starszych lub używanych samochodów będzie wykazywać bardzo sprężyste zawieszenie. Jadąc po wyboistej drodze samochód będzie podskakiwał i trudno jest go kontrolować. Koła często opuszczają ziemie gdy samochód podskakuje. Najbardziej doświadczeni kierowcy zdają sobie sprawę ,że samochód potrzebuje nowych amortyzatorów. Ale co dokładnie się tu dzieje? Masa samochodu się nie zmienia. Sprężyny (stała sprężyny K), zainstalowane fabrycznie nowe dla każdego koła, nie uległy zmianie . Amortyzatory wyglądają jak rurki, znajdujące się wewnątrz sprężyny śrubowej każdego koła. Amortyzatory są wypełnione lepkim płynem i zapewniają oporność na ruch , gdy opony odbijają się od dziur. Wykazują one współczynnik tarcia płynnego B. Niestety amortyzatory mogą wytworzyć wewnętrzne nieszczelności, a wartość B maleje. Kiedy tak się dzieje, przeregulowanie systemu drugiego rzędu staje się zbyt duże, a koła zaczynają odrywać się od ziemi. Wymiana amortyzatorów przywraca pierwotną wartość B i przywraca z powrotem poziomy projektowane. Większe samochody mają większą masę, większe sprężyny i mają większe wstrząsy.
Przejdźmy do czwartego celu
Jak uzyskać optymalną wydajność z robota
Wymagania dla systemów drugiego rzędu mogą różnić się w zależności od miejsca. Możemy potrzebować szybkiego czasu narastania; możemy potrzebować cichego systemu, który zbytnio nie oscyluje; możemy potrzebować zminimalizować masę lub inny parametr projektowy. Nie zapomnij , że ω i δ są parametrami dziedziczonymi z m , K i B. Możesz utknąć z jedną lub więcej z tych pięciu parametrów i żyć z nimi. Na przykład, masa m może być ustawiona przez ładunek , stałą sprężystości K może być nieodłączna w zawieszeniu, a tarcie B może być ustawione przez środowisko. W wielu systemach wymagania często są ze sobą sprzeczne , a kompromisy muszą zostać podjęte. W takim projekcie, często trudno ustalić co dalej. Przyjrzyj się dokładnie rysunkowi "Tylko Różne Tłumienie". Pokazuje cztery krzywe, w tym najniższą przy wartości tłumienia 0,99. Układ drugiego rzędu ze stałą tłumienia bliską 1 nazywany jest "krytycznie tłumionym". System wznosi się bezpośrednio do poziomu Nie ma przekroczenia ani nie występuje nadmierny skok. To prawda ,że czas narastania nie jest niczym nadzwyczajnym, ale system jest bardzo stabilny i cichy. Projektowanie systemu , który ma być krytycznie tłumiony, jest dobrym wyborem, jeśli nie ma innego definiowalnego celu dla jego wydajności. To bardzo bezpieczny zakład. W praktyce sensowne jest wycofanie się ze stałej tłumienia równej 1, ponieważ nadmiernie tłumiony układ jest trochę powolny. Jeśli możesz pozwolić sobie na pewne przeregulowanie rozważ stała tłumienia między 0,5 a 0.9
Uwagi Na Temat Projektowania Robotów
Podczas projektowania robota należy wziąć pod uwagę kilka czynników. Wymieniamy je tutaj bez szczególnej kolejności.
Projektowanie Prześwitu
Samochody oferują wspaniałe przykłady projektów systemu drugiego rzędu. Projektant samochodu może zostać poproszony o zaprojektowanie lekkiego samochodu o płynnej jeździe. Zwykle lekki samochód będzie się trochę odbijał ,tylko dlatego ,że jest mniejszy. Doprowadzając tą wizję do ekstremum, rozważmy samochód tak mały ,że musi wjechać do dziury, zanim zdąży podjechać na drugą stronę i wydostać się z niej. Z pewnością lżejszy samochód będzie cierpiał z powodu wybojów na drogach niż cięższy samochód, ale jest w tym coś więcej. Kiedy samochód posuwa się przez dziury , sprężyny i zawieszenie usiłują pochłonąć uderzenie i ochronić pasażerów przed wstrząsami. Ale jeśli sprężyny osiągną maksimum (tak jak w przypadku głębokiej dziury) , stają się one nielinearne. W tej sytuacji model drugiego rzędu ulega rozpadowi, stała sprężyny staje się dość duża a wszystkie uderzenia są przenoszone bezpośrednio na pasażerów i resztę samochodu. W ten sposób zginasz felgi, niszczysz ustawienia i dostajesz skurczu szyi ! Do nas, projektantów , należy upewnienie się ,że system drugiego rzędu ma wystarczającą ilość miejsca, aby uniknąć tych problemów. Jeśli Twój robot ma przenosić jajka do domu z kurnika, upewnij się ,że zawieszenie jest dobre
Nieliniowe Elementy Sterujące
Do tej pory w naszych obliczeniach i matematyce założyliśmy, że wszystkie elementy sterujące zachowują się liniowo. Bardzo dokładnie określone, zakładają płynne, ciągłe działanie bez gwałtownych ruchów. Wprowadzając definicję z rachunku różniczkowego, ten ruch liniowy charakteryzuje się krzywymi ze skończonymi pochodnymi. Poniższy rysunek pokazuje ciągłą krzywą i nieciągłą krzywą
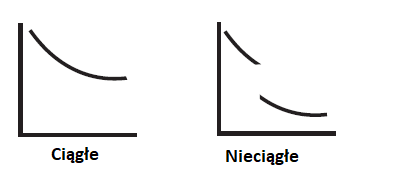
Wyobraź sobie na chwilę wysyłanie robota przez teren opisany przez każdą krzywą, a łatwo będzie sobie wyobrazić , dlaczego powinniśmy wziąć pod uwagę nieliniowe elementy sterujące w tej dyskusji. Musimy być gotowi na radzenie sobie z takimi sprawami, ponieważ większość robotów ma jakieś nieliniowe elementy gdzieś w obrębie projektu. Często te elementy są nieodłączne w mechanice lub wpełzają co systemu sterowania, kiedy najmniej się tego spodziewamy. Rozważmy przypadek aktywatora lub czujników, które są włączone lub wyłączone. Są one Ci już znane:
• Termostaty. Piece w większości domów nie mogą być obsługiwane w połowie. Palniki nie mają ustawienia średniego jak kuchenka. Albo grzejnik jest całkowicie włączony albo grzejnik jest wyłączony. Termostat reprezentuje sygnał wejściowy sterowania sprzężeniem zwrotnym czujnika. Włącza on ogrzewanie , dopóki temperatura na termostacie nie przekroczy ustawionej temperatury. Następnie wyłącza ciepło, aż temperatura nie spadnie poniżej ustawionej temperatury. Jest drogie i nieefektywne (jeśli chodzi o spalanie), aby zapalić piec i najlepiej jeśli będzie działało przez jakiś czas po zapaleniu. Wynik netto jest taki ,że temperatura w pomieszczeniu nie trzyma jednej temperatury. Zamiast tego zmienia się w górę i w dół wokół ustawionej na tarczy. To działanie, podjęta przez wiele systemów sterowania nazywa się polowaniem. Wkrótce porozmawiamy o polowaniu. To działanie polowania systemu grzewczego jest po prostu w dobre w konstrukcji termostatu. Ludzie na ogół nie wyczuwają ani nie przejmują się wahaniami temperatury wokół nastawy. Ale rozważmy regulator światła. Jeśli regulator włączał i wyłączał by światło pięć razy na sekundę, czytanie byłoby raczej trudne. Zamiast tego regulatory włączają i wyłączają światło około 60 razy na sekundę więc ludzkie oko nie wykrywa fluktuacji. Kiedy projektujesz system , który będzie polował na wyjściu, upewnij się ,że znasz te wymagania.
• Mechaniczne uszkodzenia. Wiele systemów mechanicznych ma luźne części, które się ślizgają, a następnie zaczepiają. W modelowym systemie drugiego rzędu rozważ, co się stanie, jeśli ciężar zostanie przymocowany do sprężyny zbyt luźną śrubą. Gdy ciężar zmienia kierunek, śruba obluzowuje się na chwilę, a następnie ponownie chwyta. Stała sprężyny faktycznie zmienia się gwałtownie wraz z upływem czasu, a płynna reakcja układu jest zakłócona. Możesz modelować wydajność robota, biorąc pod uwagę, że system modelu będzie działał na dwa różne sposoby. Gdy śruba zostanie uchwycona, stała sprężyny jest zgodna z projektem. Kiedy śruba jest poluzowana , stała sprężyny jest równa 0. Jeśli taki model matematyczny jest zbyt trudny do wykreślenia, możesz skorzystać z poniższego skrótu. Wystarczy zastanowić się nas dodaniem mechanicznej odległości do pokonania (odległość ,na jaką masa porusza się swobodnie przez śrubę) aż do przekroczenia i spadku. Staraj się minimalizować mechaniczne niestabilności robota
• Cyfrowe siłowniki. Wiele siłowników i czujników ma zazwyczaj charakter cyfrowy. Rozważmy solenoid. Jest to w zasadzie elektromagnes ciągnący żelazny ślimak do środka magnesu. Jest włączony lub wyłączony. Żelazny ślimak zapewnia ciągnięcie drugiego układu, gdy elektromagnes jest aktywowany. Skutecznie, nasz model systemu drugiego rzędu jest dobry do przewidywania zachowania systemu, ponieważ solenoid zachowuje się jak wejście krokowe.
Polowanie
Widzieliśmy w przypadku systemu sterowania ogrzewaniem termostatycznym, że wyjście systemu będzie polowało, skutecznie cyklicznie w górę i w dół nastawy temperatury, bez ustalenia wartości końcowej. W liniowych układach sterowania o dużej mocy i słabych punktacji w odpowiedzi wysokoczęstotliwościowej, odpowiedź wyjściowa będzie miała na sobie falę sinusoidalną. To zakłócenie może być dość denerwujące, podobnie jak brzęczenie w systemie stereo. Jest mało prawdopodobne , że oscylacje będą przy ? , chyba ,że rządzi nim element nieliniowy w systemie. Pomyśl przez chwilę jak denerwujące byłoby otwarcie drzwi windy a wysokość windy oscylował w górę i w dół podczas próby wysiadania! W wielu systemach polowanie nie jest akceptowalne. Zachowania takiego można uniknąć powstrzymując się od używania elementów nieliniowych:
- Cyfrowe siłowniki , które są włączone-wyłączone (jak solenoid) wprowadzają ruch nieliniowy do systemu
- Nie używaj cyfrowych sensorów, które raportują włączenie i wyłączenie. Czujniki , które włączają nocne światła, są właśnie takie. Nie włączają one światła powoli, w miarę zapadania ciemności.
- Unikaj mechanicznych uszkodzeń. Części mechaniczne robota mogą poruszyć się , jeśli śruby nie zostały dokręcone. System sterowania nie może tego zrekompensować bardzo dobrze
- Zmniejsz ω. Często jeśli zmniejszamy pasmo przenoszenia systemu, możemy uniknąć oscylacji. Oczywiście odbywa się to kosztem wolniejszej wydajności
- Dodajemy element histerezy do układu sterowania; taki element jest zdefiniowany jako "opóźnienie efektu kiedy działające siły na ciało zostają zmienione". Powszechnym sposobem patrzenia na element histerezy jest to ,że zachowują się inaczej w zależności od kierunku. Zawieramy tu kilka elementów nieliniowych układu sterowania, które możemy stworzyć dla grupowania z tematem histerezy. Oto kilka przykładów elementów histerezy:
* Blok cierny, który ciągnie łatwiej w jednym kierunku niż innym
* System sprężynowy, który uruchamia dwie sprężyny podczas ruchu w jednym kierunku, ale zwalnia jedną sprężynę , gdy porusza się w drugą stronę
* Obiekt z mechanizmem zapadkowym, dzięki czemu łatwo przesuwa się o jeden znak podziałki w jednym kierunku, ale nie przesuwa się o jeden znacznik w drugą stronę , chyba że zostanie zmuszony do przesunięcia dwóch znaczników podziałki w ten sposób. Taki system świetnie się nadaje do utrzymywania przedmiotu w stanie nieomal równowagi.
- Uzyskanie zmiany na podstawie pozycji to kolejny przykład. Windy zazwyczaj mają potężne silniki ciągnące je w górę i w dół, gdy znajdują się między piętrami. Gdy zbliżają się do żądanego piętram przełączają się na silniki o mniejszej mocy, aby dokonać ostatecznej regulacji przed zatrzymanie. Kiedy drzwi się otwierają , mogą nawet całkowicie wyłączyć silniki. Tego rodzaju zmiany znacznie ułatwiają unikanie polowań w końcowej pozycji systemu sterowania
Ostrzeżenie
Do tej pory mówiliśmy o systemach sterowania robotami w bardzo abstrakcyjny sposób. Równania pokazują bardzo ładnie, że nasza matematyka będzie w czysty sposób kontrolować pozycję robota w bardzo przewidywalny sposób. Co więcej, możemy z zadowoleniem wprowadzić niewielkie zmiany parametryczne w równaniu a nasz robot będzie błogo zmieniał swój sposób działania. Cóż , bardzo łatwo jest się zgubić w tak matematycznie idealnym świecie. Przez cały czas opracowywaliśmy i planowaliśmy zbudowanie i sterowanie systemem sterowania drugiego rzędu. Zrobiliśmy to całkiem nieźle. Kłopot w tym ,że nasz model nigdy nie pasuje dokładnie do robota, który budujemy. Mamy matematyczny system sterowania, który będzie kontrolował pojedynczą zmienną, taką jak pozycja naszego robota, do wymaganej precyzji. Jednak nie będzie to jedyny wymóg, który musimy spełnić. Po drodze zignorowaliśmy inne nieokreślone wymagania. Aby spełnić te inne , być może będziemy musieli zmienić zachowanie naszego prostego systemu sterowania lub będziemy musieli wprowadzić jeszcze więcej kontroli. Poniższa sekcja o systemach sterowania wielowymiarowego mówi nieco o tym zagadnieniu . Oto kilka wymagań jakie mogą się pojawić
• Szybkość. Świetnie, zaprojektowaliśmy nasz system kontroli położenia, tak aby nasz robot przesunął się tam gdzie należy. Ale co z pułapkami szybkości? Prędkość jest pierwszą pochodną pozycji. W żargonie zmiennych , których używaliśmy v= dx/dt. Na razie tak naprawdę nie martwiliśmy się o prędkość. Jest to oczywiście częściowo związane z czasem narastania zmiennej pozycji . Im szybciej układ sterowania reaguje na zmiany pozycji, tym szybciej może pójść. Ale będą różne ograniczenia szybkości:
- Bezpieczeństwo. Czasami nie jest bezpiecznie, gdy robot porusza się z większą prędkością
- Moc. Czasami marnowanie czasu jest zbyt szybkie. Niektóre silniki i sterownik nie są tak wydajne przy maksymalnej szybkości
- Manewrowanie. Niektóre roboty nie skręcają dobrze. Zaleca się zwalniać na zakrętach.
-
• Przyspieszenie. Dobrze, zaprojektowaliśmy nasz system kontroli prędkości ,aby nasz robot mógł nie przyspieszać lub być zagrożeniem. Ale co zrobić z przyspieszeniem?
Przyspieszenie jest pierwszą pochodną prędkości i drugą pochodną pozycji. W mowie zmiennych, z których korzystamy
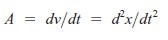
Do tej pory tak naprawdę nie martwiliśmy się o przyspieszenie. Ale różne ograniczenie przy przyspieszeniu mogą mieć miejsce:
- Koła trakcyjne, jeśli są używane mogą przyspieszyć robota. Poza trakcją zapewnianą przez koła, robot będzie palił gumę
- Balans. Robot może jeździć na jednym kole
- Naprężenia mechaniczne. Przyspieszenie działa na wszystkie części robota. Robot może oderwać istotną część, jeśli przyspiesza zbyt szybko.
- Mechaniczne uszkodzenia. Robot zmienia kształt, gdy przyspiesza. Dzieje się to w luźnych łączach i połączeniach
System Sterowania Z Wielu Zmiennymi
Do tego momentu próbowaliśmy zbudować system sterowania robotem, który mógłby służyć do utrzymywania pojedynczej zmienne , takiej jak pozycja .Powinniśmy przyznać ,że matematyka systemu sterowania jest bardzo ogólna i ma zastosowanie również do robotów, które chcą kontrolować inne pojedyncze zmienne, takie jak prędkość lub przyspieszenie. Chociaż systemy kontroli tempomatu są bardzo złożone , są to po prostu systemy sterowania , które regulują prędkość w zależności od potrzeb kierowcy. Ale co się stanie jeśli chcemy kontrolować jednocześnie dwie lub więcej zmiennych? Załóżmy
,że chcemy aby robot podążał za czarną linią i poruszał z bezpieczną prędkością. Kontrola zarówno pozycji (względem czarnej linii), jak i prędkości (aby robot nie zmieniał kierunku zbyt szybko z dużą prędkością) pozwala nam kontrolować dwie zmienne w tym samym czasie. Jak to robimy?
Jednym z rozwiązań jest umieszczenie dwóch osobnych systemów sterowania w robocie. Jeden system będzie sterował położeniem względem czarnej linii. Drugi system sterowania upewnia się ,że robot porusza się z odpowiednią prędkością. Taki system kontroli jest z natury rozproszonym systemem kontroli, takim jak te, które omówiliśmy wcześniej. W rzeczywistości auta mają wiele komputerów obsługujących te zadania. Każdy system sterowania ma własny zestaw problemów , które omówiliśmy, takich jak stan błędu stabilnego, przekroczenie, dzwonienie i czas ustalania Jednakże, jak mówiliśmy, w sekcji dotyczącej rozproszonych systemów kontroli ,sytuacja może się bardzo skomplikować. Oto kilka punktów do rozważenia:
• Czy ma sens spowalnianie robota jeśli znajduje się on bardzo daleko od czarnej linii?
• Czy przydałoby się przyspieszyć, jeśli robot zmierza w dobrym kierunku przez długi czas?
• Co robimy , jeśli jeden z systemów kontroli stwierdzi ,że jest całkowicie poza kontrolą? Jeśli straci ślad czarnej linii, czy powinien zwolnić?
• Jeśli robot porusza się bardzo szybko, czy musimy szukać czarnej linii na zakrętach?
Wszystkie scenariusze przemawiają za przesyłaniem informacji tam i z powrotem między dwoma systemami kontroli. Co więcej, sposoby interakcji między nimi mogą stać się bardziej złożone. W
pewnym momencie, jeśli do robota dodanych zostanie coraz więcej systemów sterowania, może wystąpić co następuje:
• Wiele systemów kontroli staje się drogie
• Komunikacją między systemami sterowania może być droga i spowalniającą. W najgorszym przypadku mogą wystąpić błędy komunikacji
• Interakcje między systemami mogą stać się nieprzewidywalne. W najgorszych przypadkach mogą powstać niestabilności. Te niestabilności mogą przybrać formę nieoczekiwanych opóźnień lub atakowania. Atakowanie powstaje wtedy kiedy dwa systemy kontroli nie zgadzają się i walczą o kontrolę nad częściami systemu. Każdy system sterowania widzi działania drugiego jako tworzącego błąd
• Projekty mogą stać się bardzo złożone, aby uwzględnić wszystkie przypadki
• Projekty mogą być trudne do zarządzania. Gdy jeden system sterowania zostanie zmieniony, inne systemy mogą przestać funkcjonować. Ponowne testowanie staje się dużym zadaniem.
Wiele lat temu, inżynierowie zaczęli rozważać systemy kontroli, które mają więcej niż jedną zmienną. Musimy tylko popatrzeć na stare rysunki silników parowych aby to docenić. Musieli regulować szybkość, ciśnienie, temperaturę i kilka innych zmiennych w tym samym czasie. Ogólne podejście polegał wówczas na wprowadzeniu w razie potrzeby wielu mechanicznych układów sterowania z blokadami. Awaria oznaczała wybuch!
Regulator prędkości,
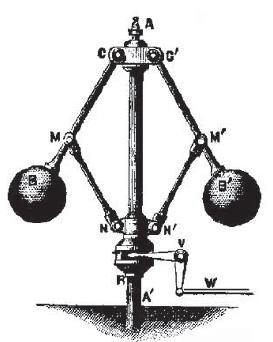
jest doskonałym przykładem użytej inżynierii mechanicznej ,dla rozwiązania problemu systemu sterowania. Reguluje szybkość silnika. Wraz ze wzrostem szybkości silnika obie metalowe kulki wirują wokół pionowego wału . Ponieważ zewnętrzna siła odśrodkowa wzrasta, kule zaczynają się poruszać na zewnątrz, ciągnąc za sobą ukośne rozpórki. Ukośne rozpórki , jeśli zostaną wyjątkowo mocno rozciągnięte, podciągną podstawę i wyzwolą nieco ciśnienia pary. Dzięki temu, silnik nie jedzie zbyt szybko. To dobry przykład oddzielnego systemu sterowania prędkością. Kilka lat później inżynierowie zaczęli myśleć o scentralizowaniu systemów sterowania. Elektronika komputerowa ułatwia to przejście
ponieważ wszystkie informacje można łatwo zebrać w jednym miejscu i zmanipulować. Inżynierowie wybrali sposób kontrolowania wielu zmiennych w tym samym czasie i poruszyli kilka kluczowych pytań:
• Jak zaprojektować system wielu zmiennych? Jakie ma mieć ramy?
• Ile zmiennych może kontrolować w tym samym czasie? Jaki ekwiwalent istnieje dla "błędu stanu ustalonego" w systemie wielu zmiennych?
• Jak oceniamy względny stan systemu sterowania? Jak daleko jest od optymalnego stanu kontroli? Jaki jest sygnał błędu?
• Jak możemy zmienić projekt systemu aby wpłynąć na jego wydajność?
Spójrzmy na pierwsze z tych pytań
Jak zaprojektować system wielu zmiennych? Jakie ma mieć ramy?
Załóżmy dla uproszczenia ,że próbujemy zaprojektować system sterujący dla sterowania tylko dwóch zmiennych w tym samym czasie: X1 i X2 (być może pozycja i prędkość). Poniższą dyskusję można uogólnić na n zmiennych (X1, X2, X3 … Xn). Możemy nazwać kombinację zmiennych X1 i X2, wektorem
X. Załóżmy , że pożądany stan tych dwóch zmiennych jest następujący:
• X1 = X1d
• X2 = X2d
Możemy nazwać pożądany stan wektora X, wektorem Xd. Jeśli w systemie sterowania są używane komputery, komputer okresowo znajduje sposób na zmianę X w oparciu o wartość Xd. W takim systemie sterowania , mówimy o obliczeniach wykonywanych okresowo, sekwencyjnych czasach oznaczonych t-1, t, t+1, itd. Użyjemy następującej notacji
• X(t-1) pokazuje wartości X w poprzednim czasie obliczeniowym
• X(t) pokazuje wartości w obocznym czasie obliczeniowym
• X(t+1) pokazuje wartości X w kolejnym czasie obliczeniowym
Podobnie Xd(t) reprezentuje szereg czasowy wartości dla Xd. Aby na przykład obliczyć następną wartość X1, na przykład, komputer obejrzy poprzednią i przedstawia wartości zarówno X1 jak i X2, i określi w jaki sposób zmienić X1 w sposób przyrostowy. Takie samo obliczenie wykonujemy dla X2. Wykonane poprawnie, X1 i X2 będzie powoli śledzić pożądane wartości. Ale jak mamy znaleźć iterację? Iteracja jest procesem powtarzania obliczeń w sposób okresowy w celu osiągnięcia określonego celu. Zwykle równania iteracyjne reguluje proces iteracji. Poniżej znajduje się równanie iteracji ogólnego przeznaczenie, które jest często używane w robotach. X(t) jest wyliczane przez iterację przez przyjmowanie wartości w czasie t i iterowanie do następnej wartości w czasie t+1:
X(t+1) = X(t) - S(t) x (dC(X(t)) / d(X(t))
W tym równaniu S(t) jest wektorem wielkości kroku , który może zmieniać się z czasem , ale może być stały. Ten wektor może zawierać w naszym przykładzie dwie stałe wartości wielkości kroku, każda z grubsza proporcjonalna do 5 procent średniej wielkości X1 i X2. Alternatywna metoda może sprawić, że wektor będzie zawierał dwie zmienne wartości wielkości kroku, , z grubsza proporcjonalne do 5 procent aktualnych wartości X1 i X2. Chodzi o to ,że X1 i X2 zmieniają się stopniowo w określonym kierunku, aby spełnić wymagania systemu sterowania. Jeśli funkcja kosztów C(Xt)) pokazuje ,że X1 musi wzrosnąć, to iteracja czasu równania spowoduje przesunięcie X1 o wielkość kroku. Jeśli funkcja kosztu pokazuje ,że X2 musi się zmniejszyć, to iteracja czasu równania spowoduje przesunięcie X2 o wielkość kroku. C(X(t)), wektor funkcji kosztowych oparty na X(t), nie ostał jeszcze zdefiniowany. Funkcja kosztu jest miarą "bólu", którego doświadcza system sterowania, ponieważ wartości (przeszłe
i przyszłe) X(t) nie pasują do pożądanych wartości Xd(t). Używamy pochodnej (d C(X(t))/dX(t)) ponieważ chcemy mieć rozmiar kroku korekcyjnego.
• Będzie większy jeśli koszt (ból) rośnie szybko, gdy X(t) zmienia się w niewłaściwy sposób. Dlatego musimy podjąć bardziej drastyczne działania naprawcze
• Będzie mniejsze jeśli koszt (ból) nie rośnie szybko, ponieważ X(t) zmienia się właściwie. Jesteśmy blisko pożądanego obszaru operacji i nie odczuwamy bólu więc po co się dużo ruszać?
Takie równanie iteracyjne może wykorzystać jako rozwiązanie do sterowania robotycznego. Ale co jeśli brakuje funkcji kosztów. Właściwy wybór funkcji kosztowej naprawdę determinuje zachowanie robota. Wiele współczesnych prac nad systemami sterowania obraca się wokół wyboru funkcji kosztowej i sposobu jej użycia podczas iteracji. Jedną z bardzo popularnych ram zapewniających system sterowania jest struktura najmniejszych kwadratów (LMS) , odkryta przez Legendre'a i Gaussa na początku XIX wieku. Wyznaczenie algorytmu najmniejszego ,średniego kwadratu (LSM), ustawia funkcję kosztu C(X(t)), proporcjonalną do sumy kwadratów błędów w każdym elemencie wektora:
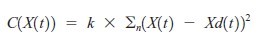
gdzie k jest dowolną stałą skalowania. W naszym konkretnym przykładzie możemy ustawić funkcję kosztów na sumę kwadratów błędów:
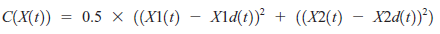
Różniczkując X1 i X2 , uzyskujemy dwa elementy z (d(C(X(t))) / dX(t)) :
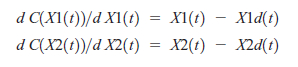
Funkcja kosztu zwiększa wielkość jako kwadrat błędów. Wielkość kroku, używana do odzyskiwania po błędach, a następnie zwiększa się liniowo proporcjonalnie do błędu. W szczególności wtedy gdy:
X(t+1) = X(t) - S(t) x (d C(X(t))/dx(t))
mamy dwa elementy iterowane w następujący sposób:
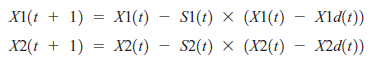
Gdybyśmy mieli ustawić rozmiary kroków S1(t) = S2(t) - 0,1 wtedy
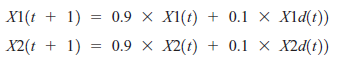
Zatem X1 i X2 powoli poszukują wartości X1d i X2d. Również X(t) powoli wyszukuje wartości Xd(t). Zanim przyjrzymy się funkcjom kosztów inaczej niż przez LMS, zakończymy odpowiadając na kilka innych pytań jakie postawiliśmy wcześniej.
Jak wiele zmiennych można kontrolować w tym samym czasie?
Praktycznie rzecz biorąc, algorytm LMS może obsługiwać dowolną liczbę zmiennych symultanicznych. Jednak ,wraz ze wzrostem liczby zmiennych drastycznie wzrasta niebezpieczeństwo interakcji. Podstawowym niebezpieczeństwem jest to ,że nieznane interakcje między zmiennymi odrzucają obliczenia i destabilizują system sterowania. To często pojawia się w matematyce, jeśli zmienne nie są całkowicie niezależne. W naszym przykładzie pochodna z X1 względem X2 może nie być prawdziwa dla zera lub vice versa. To znacznie pogorszyłoby stabilność iteracji stopniowych. Zgodnie z ogólną zasadą, staraj się nie używać jednego systemu sterowania do obsługi zbyt wielu zmiennych w tym samym czasie. Dwie do czterech zmiennych jest dobrym miejscem do zatrzymania się
Jaki ekwiwalent istnieje dla "błędu stanu ustalonego" w systemie wielu zmiennych?
Po pierwsze, gdy istnieje wiele zmiennych, należy pamiętać ,że jest to całkowicie możliwe, że system nigdy nie osiągnie stanu ustalonego. Jednak obliczenia cyfrowe mogą się znaleźć w całkowicie stabilnym i cichym rozwiązaniu. Takie rozwiązanie miałoby X(t) stałe i równe Xd(t). Jednak przy pewnych minimalnych rozmiarach kroku, może nie być możliwe zbieżność z cichym rozwiązaniem. Takie rozwiązanie miałoby X(t) stabilnych i równych Xd(t). Pomyśl przez minutę o systemie przy 9, szukając 10, minimalnym krokiem 2 w tył i przód. System będzie prawdopodobnie wahał się między 9 a 11 i z powrotem do 9. Starannie opracowany algorytm sterowania pozwala uniknąć takiego problemu.
Jak oceniamy względny stan systemu sterowania? Jak daleko jest od optymalnego stanu kontroli? Jaki jest sygnał błędu?
W przypadku systemu LMS można śledzić rozmiar funkcji kosztu. Wszystkie warunki w sumie są dodatnimi, liczbami kwadratowymi. Wielkość może być używana jako miara stanu systemu. Chcemy wyraźnie aby był mały. Ponadto, pierwsza pochodna funkcji kosztu powinna być cicha. Względny poziom hałasu , funkcja kosztu jest miarą zmienności systemu i może być wykorzystany do wskazania zakłóceń na wejściach systemu.
Jak możemy zmienić projekt systemu aby wpłynąć na jego wydajność?
Algorytm LMS jest względnie prosty z następujących powodów:
• Możemy zachować rozmiar kroku w wektorze S(t) jako stały. Jeśli rozmiary kroku waha się od 0 do 1, szybkość odpowiedzi systemu zmienia się od lodowatego do króliczka. Musimy uznać
,że systemy sterujące typu króliczek ,mają zbyt wysoką częstotliwość i są podatne na przeregulowanie , dzwonienie i niestabilność. Dobrym pomysłem jest sprawienie ,aby twój robot pracował na wartościach S(t)
• Możemy zmienić wielkość kroku w wektorze S(t), aby zachować stan spoczynkowy systemu. Sposób w jaki to robi, musi być wybierany z wielką ostrożnością, aby uniknąć dodawania hałasu do systemu. Dobrym rozwiązaniem jest zmniejszenie rozmiarów kroków, gdy system zaczyna się wyciszać, i zwiększać rozmiar kroków (w granicach rozsądku) , ponieważ system zaczyna hałasować i jest aktywny.
• Możemy zmieniać rozmiary kroków w taki sposób, aby zawsze były potęgą 2 . Mnożenie (lub dzielenie) przez potęgę dwa wymaga tylko prostej operacji zmiany arytmetyki binarnej. Ograniczenie rozmiaru kroków do takich wartości może znacznie ułatwić obliczenia LMS dla mniejszych mikrokomputerów.
• Możemy ustawić rozmiar kroków na 0 gdy funkcja kosztu jest wystarczająco mała. Zabiega to zakłóceniom w pobliżu optymalnego rozwiązania. Takie zakłócenie może być spowodowane szumem wejściowym i niewielkimi efektami arytmetycznymi. Wyobraź sobie windę otwierającą drzwi. Pasażerowie nie są zainteresowani uzyskaniem dokładnie poziomu podłogi,o ile jest wystarczająco blisko. Pasażerowie byliby naprawdę niezadowoleni gdyby system sterujący windy wciąż poruszał się w górę i w dół , próbując to naprawić. Zamiast tego, systemy sterujące windy zatrzymają wszystkie działania po otwarciu drzwi. Możemy osiągnąć podobny efekt , ustawiając rozmiar kroku na 9. Później przyjrzymy się innym kwestiom bezpieczeństwa.
Funkcje Kosztów NIE-LMS
Algorytm sterowania, taki jak LMS. ma cechy behawioralne, które wpływają na sposób w jaki robot będzie się zachowywał:
• System sterujący LMS mają tendencję do reagowania wolniej na dane wejściowe. Zazwyczaj oznacza to ,że mają wolniejszy czas reakcji
• Systemy sterujące LMS są bardziej stabilne w obliczu szumu na wejściach
• Matematyka nie jest trudna i nie zużywa cennych zasobów komputera
Dostępne są funkcje kosztowe poza LMS. LMS wciąż wymaga mnożenia, które mogą pochłaniać czas i zasoby komputera. LMS mnoży rozmiar kroku przez błąd różnicowy (X1 - X1d),aby uzyskać wielkość kroku iteracji. Można do tego podejść w inny sposób:
• Używaj tylko znaku (X1 - X1d) a nie wielkości. Znak po prostu wskazuje w jaki sposób X1 jest wyłączone. Cały rozmiar kroku jest po prostu dodawany lub odejmowany od X1 dla iteracji do kolejnej wartości. To sprawia ,że krok iteracji jest prostym dodawaniem lub odejmowaniem i unikamy mnożenia. Może to być szczególnie cenne , jeśli wybierzemy mały mikrokomputer ,który nie ma mnożnika.
• Używamy względnego rozmiaru (X1-X1d) aby wybrać rozmiar kroku z tabeli rozmiaru kroków. Może to działać dobrze, a także pozwala unikać mnożenia. Może zbiegać się szybciej gdy funkcja kosztów jest duża i może pozostać dość cicha w kwestii optymalnego rozwiązania.
Systemy z wieloma zmiennymi mają również inne szczególne cechy. Zagadnienie stabilności, zbieżności i szybkości działania muszą być omówione tutaj:
• Stabilność. Jak już wspomniano, jeśli rozmiar kroku jest zbyt duży, system może oscylować wokół punktu rozwiązania w sposób niedopuszczalny. Ponadto wszystkie zmienne mogą nie być w stanie osiągnąć optymalnego rozwiązania w tym samym czasie. System może pozostać głośny na zawsze, nawet jeśli dane wejściowe przestaną się poruszać.
• Konwergencja. W niektórych sytuacjach system sterowani nie działa, przechodząc do akceptowalnego rozwiązania:
- Znajdowanie rozwiązania. Czasami pozycja początkowa robota może wpływać na to ,czy przeniesie się do wybranej lokalizacji czy nie. System sterowania zawsze ma zbiór punktów, poza którymi nie może odzyskać. Podczas projektowania i działania naszego systemu sterowania robotem musimy upewnić się ,że robot nie zostanie poproszony o odzyskiwanie w takiej sytuacji. Zauważ ,że musimy ustalić co jest akceptowalnym rozwiązaniem dla robota. Często wiąże się to z pewnym parametrami dotyczącymi wielkości funkcji kosztu, ale można tego dokonać na wiele różnych sposobów.
- Unikanie fałszywych rozwiązań. Czasami systemy arytmetyczne będą ustawiać się na fałszywym rozwiązaniu. Przykładem może być robot szukający najwyższego wzniesienia, aby znaleźć mniejsze wzgórze w pobliżu. Jeśli system sterowania musi radzić sobie ze złożonym środowiskiem, może się to wydarzyć łatwiej niż można podejrzewać. Jeśli sytuacja wygląda podejrzanie, zastanów się nad wprowadzeniem jakiegoś mechanizmu bezpieczeństwa dla systemu sterowania, który wyrzuci robota z fałszywego rozwiązania jeśli utknie w jednym. Taki
system "bezpieczeństwa" musi być bardzo dobrze zaprojektowany, aby upewnić się ,że nie tworzy on fałszywego alarmu i nie zakłóca dobrego rozwiązania
- Szybkość działania. Tak jak w przypadku każdego systemu sterowania robotem, zawsze spodziewana jest dobra wydajność. Szybkość działania jest prawie zawsze w jednym z kryteriów. Jeśli rozmiary kroku są zbyt małe. może zająć niewiarygodnie długo, aby przejść do właściwego rozwiązania. Wybierz wielkość kroku aby zoptymalizować zachowanie robota pod względem szybkości i dokładności. Rozważ wybór rozmiaru kroku, aby najlepiej pasował do możliwości poruszania się i manewru robota. Jeśli wzorzec jest bliski, wyniki będą lepsze w postaci płynniejszej operacji.
Teraz potrzebujemy trochę nagrody za przebrnięcie przez tak "użyteczną" matematykę .Czas trochę pomarzyć i porozmawiać o bardziej ezoterycznych sprawach, które mogą na nas nie wpłynąć dziś lub jutro, ale i tak są ważne.
Czas
Nieco mówiliśmy o tym ,ze nie można liczyć na to ,że Ziemia będzie stabilnym punktem odniesienia da naszego robota. Z praktycznego punktu widzenia jest wystarczająco stabilna w każdym przypadku. Ale za to Albert Einstein podrzuca nam kolejną zasłonę dymną. Okazuje się , że nie możemy liczyć na to ,że sam czas będzie niezmienny w naszych obliczeniach. Jeśli jednak robot porusza się z małą szybkością i pozostaje z dala od czarnych dziur, prawdopodobnie możemy zignorować następujące rozważania. Jeśli robot będzie poruszał się z dużymi prędkościami w stosunku do Ziemi, wtedy obliczenia Einsteina wchodzą w grę. Na początku XX wieku Einstein, wy wymyślił specjalną teorię względności, która utrzymuje ,ze czas nie zawsze biegnie w tym samym tempie. Jeśli dwa ciała poruszają się względem siebie, doświadczą czasu z dwiema różnymi współczynnikami. Efekt nie staje się poważny, dopóki prędkości nie są wysokie. Ale nawet astronauci okrążający Ziemię, muszą wziąć pod uwagę czas relatywistyczny lub ich obliczenia wyłączone będą wyłączone. Czas zmienia się w przybliżeniu jako 1/sqrt(1-(v/c)2), gdzie v jest względną prędkością obiektu, a c jest prędkością światła. Korzystając z tego wzoru, przy prędkości orbitalnej około 8800 metrów ,i danej szybkości światła 300 000 000 metrów na sekundę, otrzymujemy rozszerzający się czas dla orbitującego statku kosmicznego

Więc rozważmy sowieckiego kosmonautę , który spędził 458 dni w kosmosie , co dało 458 x 24 x 60 x 60 = 39 571 000 sekund. Ignorując wszystkie inne ruchy statku kosmicznego inne niż prędkość orbitalną, czas rozszerzający kosmonauty 39 571 000 x 1,0000000004 = 39 571 000 017 sekund. Tak więc, po ponad roku na orbicie , dla kosmonauty nastąpiła zmiana czasu o 17 milisekund . To niewiele
,ale przy prędkości orbitalnej 8800 m/s , kosmonauta wyleciałby na 150 metrów (8800 x 0,017). To nie jest daleko, biorąc pod uwagę rozległość Ziemi, ale duży błąd podczas próby dokowania. Planiści orbitalni biorą pod uwagę efekty relatywistyczne podczas planowania orbit i misji międzyplanetarnych
Przestrzeń
Cóż, jeśli nie jest wystarczająco źle, kiedy martwisz się czym jest czas, Einstein rzucił kolejną zagwozdkę dla naszego zbiorowego myślenia. Ogólna Teoria Względności głosi ,że sama tkanka przestrzeni to nie tylko seria prostych prostopadłych linii, jak wzór ulic, ale raczej zakrzywiona i zmieniająca się! Wymyślił
tę teorię za pomocą pięknego "eksperymentu myślowego". Zamiast pracować w laboratorium, Einstein usiadł i przedstawił eksperyment w swojej głowie. Oto sposób jego myślenia. Załóżmy ,że siedzimy w pokoju w odległej przestrzeni, gdzie nie ma grawitacji. Dwie dziury znajdują się w ścianie . jedna po lewej a druga po prawej stronie. Promień światła przechodzi przez jedną ścianę i wychodzi przez drugą. Nie trzeba wiele aby wiązka przeszła przez pokój z prędkością światła. Światło przemierza 30 cm na miliardową część sekundy
Jeśli teraz przyspieszymy pokój w górę z prędkością 975 cm/sekundę/sekundę (1G grawitacji), kiedy kolejna wiązka światła przechodzi przez pierwszą dziurę, nie wydostanie się przez drugą dziurą (która jest teraz ruchoma) . Z naszego punktu widzenia ,siedzącego w pokoju , promienie światła zakrzywiają się po wejściu do pokoju i uderzają w ścianę zbyt nisko . Teraz przypuśćmy ,że zamiast przyspieszenia, natychmiast pod pokojem położyliśmy Ziemię. Z punktu widzenia siedzącego w pomieszczeniu, nie można mówić o różnicy. Nadal doświadczamy przyspieszenia 1G pod nami. Strumień światła pojawia się w pierwszym otworze i nadal zagina aby uderzyć w ścianę poniżej drugiego otworu. To grawitacja zagina światło. Ale jeśli utrzymamy ,że światło musi poruszać się w linii prostej ze stałą prędkością, to musimy stwierdzić ,że grawitacja pochyla się sama zagina przestrzeń. Samo istnienie materii, która wytwarza siłę grawitacji, zagina naszą tkaninę przestrzeni. Wydaje się dość proste, prawda? Abyś nie martwił się o swoją "wypaczoną" egzystencję, możesz mieć pewność ,ze zagięcie przestrzeni jest niewielkie i może być zignorowane w większości naszych codziennych czynności. Około pierwszej wojny światowej, niektórzy astronomowie postanowili poddać próbie ogólną teorię względności Einsteina. Obserwowali pewne znane gwiazdy podczas zaćmienia Słońca . Rzeczywiści gwiazdy pojawiły się zza Słońca i Księżyca, wcześniej niż powinny. Światło gwiazd pochodziło zza Słońca (skąd astronomowie nie powinni go zobaczyć), zakrzywiając się wokół grawitacji słońca i pojawiając się wcześniej niż powinno. Co więcej, ilość obserwowanego zaginania ściśle pasowała do teoretycznych obliczeń Einsteina. Była to rewelacja w nauce i główne odkrycie Einsteina. Kilka lat później naukowcy odkryli trzy gwiazdy z rzędu, z których dwie wyglądały identycznie. Okazało się ,że światło jednej gwiazdy było pochylone wokół gwiazdy pośredniej , więc oba obrazy ukazały się nam na Ziemi. To była kolejna manifestacja grawitacyjne zaginania światła i zostało nazwane soczewkowaniem grawitacyjnym. Ponieważ światło gwiazd może zakrzywiać się wokół gwiazdy pośredniej w dowolnym kierunku (360 stopni), soczewkowanie grawitacyjne często zapewnia obraz gwiazdy jako pierścień lub łuk światła.
•