Wielcy Matematycy | Wielcy Astronomowie | Wielcy Inżynierowie
[
1281
]
TALES (640-546 p.n.e) : Tales z Miletu jest pierwszym znanym z nazwiska greckim mędrcem. O życiu jego wiemy niewiele. Żył prawdopodobnie w latach 640-546. Starożytni pisarze nazywali go "pierwszym" filozofem, "pierwszym" fizykiem, matematykiem, astronomem
Wyrósł w bujnej atmosferze życia małoazjatyckich kolonii, w których element grecki odgrywał rolę pośrednika w handlu między Wschodem a Zachodem. Z kontaktów handlowych wywodzi się zapewne i oddziaływanie kultury babilońskiej i egipskiej na małoazjatyckich Greków. Platon wspomina ,że gdy Tales
obserwował gwiazdy, wpadł do studni i piękna niewolnica miała się wyrazić żartem, iż chciał zobaczyć, co się dzieje na niebie, a nie dostrzegł tego co znajduje się pod jego nogami. Anegdota ta jednak nie charakteryzuje postawy Talesa. Nie był on oderwanym od życia myślicielem, lecz
człowiekiem nad wyraz praktycznym, który umiał wykorzystać posiadaną wiedzę w swoich transakcjach handlowych. Prokolos, komentator pierwszej księgi Elementów Euklidesa w oparciu o zaginioną Historię geometrii Eudomesa, przypisuje Talesowi autorstwo następujących twierdzeń geometrycznych:
1.Dowód ,że średnica dzieli koło na połowy
2.Odkrycie, obok szeregu innych twierdzeń ,że kąty przypodstawne w trójkącie równoramiennym są równe
3.Twierdzenie o równości kątów wierzchołkowych i
4.O przystawaniu trójkątów o równym boku i przyległych dwu kątach.
Talesowi przypisuje się również autorstwo twierdzenia ,że kąt wpisany w półokrąg jest prosty. Jego imieniem nazwane zostało twierdzenie o proporcjonalności odcinków, jakie dwie równoległe odcinają na ramionach kąta. Wymienione twierdzenia nie stanowiły w epoce Talesa żadnej rewelacji wobec poziomu, który osiągnęła zamarła już
w owym czasie w rozwoju matematyka egipska i babilońska. Wielkość Talesa jako matematyka polega raczej na tym ,że z jego imieniem wiąże się pojęcie dowodu twierdzenia. Matematyków egipskich i babilońskich interesowało pytanie "jak". Tales zaś, o ile wiemy, pierwszy pytał "dlaczego". Nie jesteśmy dziś w stanie ustalić, jak Tales
przeprowadzał dowód. Wybitny historyk matematyki starogreckiej T Heath utrzymuje ,że tak oczywistego faktu, jak ten ,iż średnica dzieli koło na połowy, nie dowodził również Euklides; wszakże Eudemos,pisarz epoki Euklidesa, znał zapewne pojęcie dowodu i nie ma podstaw, aby odrzucić jego relację ,że Tales dowody przeprowadzał. Talesa
można uznać za tego, który łącząc teorię z praktyką zbudował fundamenty geometrii jako nauki dedukcyjnej, której ukoronowaniem były Elementy Euklidesa. Powrót
PITAGORAS (570-496 p.n.e.) : Dziś imię Pitagorasa zajmuje poczesne miejsce w historii początków myśli matematycznej starożytnej Grecji. Autorzy świata antycznego wymieniają go raczej jako działacza politycznego, proroka, cudotwórcę czy mistyka. Ksenofanes, nawiązując do jego wiary w wędrówkę dusz
,przypisuje mu słowa, które wypowiedział na widok bitego psa: "Przestań go bić, gdyż w tym psie jest dusza mojego przyjaciela, poznaję go po głosie." O samym Pitagorasie wiemy niewiele. Żył zapewne w latach 570-496, lecz prąd filozoficzno-religijny związany z jego imieniem trwał przez dwa wieki i nie sposób ustalić, co on zawdzięcza Pitagorasowi
a co jego uczniom. Mówić należy raczej o pitagoreizmie. Elementami pitagoreizmu są : muzyka,harmonia i liczba, rozpatrywane przede wszystkim jako czynniki wychowawcze, służące zbliżeniu do boga. Matematyka i mistyka liczb tworzyły w pitagoreizmie dziwny konglomerat, z którego wyrosło ścisłe poznanie matematyczne późnych pitagorejczyków, ceniących
tylko to, co mogło być dowiedzione na drodze rozumowej. W dziedzinie geometrii opracowali oni teorię równoległych wraz z twierdzeniem o sumie kątów trójkąta, czworokąta i wieloboków foremnych;badali koło, wielościany foremne i kulę. Odkryli pięciokąt foremny,wiedzieli ,że płaszczyznę można pokryć tylko następującymi wielokątami foremnymi: trójkątami
równobocznymi, kwadratami albo sześciokątami. Udowodnili twierdzenie Pitagorasa. W ich środowisku wyrosły trzy wielkie zagadnienia greckiej starożytności: podwojenie sześcianu, podział kąta na trzy równe części i kwadratura koła, przy pomocy cyrkla i liniału. Uprawiali również arytmetykę, a raczej teorię liczb, którą odróżniali od pogardzanego rachunku
arytmetycznego, zwanego logistyką. Liczby wyobrażali sobie dość konkretnie jako punkty ułożone w postaci figur geometrycznych. Aby móc odróżniać między sobą jednostki - punkty, każdy był otoczony w ich pojęciu "polem". Dzięki temu liczbę wyrażali bądź przy pomocy punktów, bądź pól kwadratowych. Wyobrażenia te naprowadziły ich na badanie liczb trójkątnych,
kwadratowych, pięciokątnych. Są to liczby, z których, o ile zostaną wyobrażone w postaci odpowiednio rozmieszczonych punktów, można ułożyć odpowiednie figury. Liczby te stanowią sumy postępów arytmetycznych:
1+2+3+...+ n = 1/2n(n+1) : liczby trójkątne
1+3+5+...+(2n-1) = n2 : liczby kwadratowe
1+4+7+...+(3n-2) = 1/2n(3n-1) : liczby pięciokątne
W związku z liczbami kwadratowymi rozpatrywali liczby postaci 2n+1, nazwane gnomicznymi, które dodane do kwadratu liczby n dają w sumie kwadrat następnej liczby. Zajmowali się również liczbami doskonałymi, to jest takimi, których suma dzielników od niej mniejszych jest równa danej liczbie, o ile 1 traktować jako dzielnik tej liczby. Takimi są np: 6,28,496,8128
Szukali również par liczb zaprzyjaźnionych, tj takich, że suma dzielników jednej z nich jest równa drugiej, np. 220 i 284. Zajmowali się proporcjami, lecz szczególne znaczenie dla dalszego rozwoju matematyki miało stwierdzenie istnienia odcinków niewspółmiernych. Odkrycie to ujawniło sprzeczności w systemie filozoficznym pitagorejczyków, według którego "wszystko
jest liczbą",rozumianą jako liczba naturalna. Podanie głosi, żę odkrycie to było utrzymywane w tajemnicy, a śmierć pitagorejczyka Hippasosa w nurtach morza tłumaczona była tym że kto usiłował na powierzchnię wydobyć to ,co skazane było na wieczne ukrycie, musiał sam ulec temu samemu losowi. Za powyższym podaniem kryje się zapewne następująca prawda historyczna. W
pitagoreizmie ścierały się dwie tendencje: naukowa i religijno-mistyczna. Pierwsza wymagała wymiany informacji między uczonymi, nie dopuszczała więc zatajania własnych wyników, druga zgodnie z obowiązującym w obrębie sekty rytuałem wymagała tajności i izolacji. Istotnie już po śmierci mistrza wymienione tendencje przeistoczyły się w dwa sprzeczne między sobą kierunki:
naukowy i religijno mistyczny. Zwolenników pierwszego kierunku nazywano matematykami - drugiego zaś akuzmatykami. Hippasos skłaniał się zapewne ku matematykom, za co został usunięty ze związku pitagorejskiego, a jego tragiczną śmierć w nurtach morza wykorzystali akuzmatycy w walce przeciwko matematykom. Zasługi tych ostatnich są dla nauki są bardzo cenne.
Powrót
EUKLIDES (ok roku 300 p.n.e) : Elementy Euklidesa są zapewne najbardziej rozpowszechnionym dziełem naukowym, którego liczba wydań od wynalezienia druku przekracza tysiąc, a wcześniejsze kopie stanowiły jedyny, używany w ówczesnym nauczaniu na odpowiednim poziomie podręcznik geometrii. Dzieło to składa się z trzynastu ksiąg
.Księgi czternasta i piętnasta są późniejszymi uzupełnieniami. Autorem czternastej jest Hipsikles z Aleksandrii (ok. 200 roku p.n.e.), a piętnastą dołączono dopiero w szóstym wieku naszej ery. Pierwsze cztery księgi i szósta dotyczą geometrii płaskiej, ostatnie trzy - przestrzennej, których ukoronowaniem są rozważania o pięciu wielościanach foremnych. Piąta jest poświęcona
teorii proporcji w ujęciu geometrycznym, której autorstwo przypisuje Proklos - Eudoksosowi. Treść księgi siódmej, ósmej i dziewiątej jest arytmetyczna. Autor wykłada w nich arytmetykę pitagorejską,a więc właściwie teorię liczb, lecz w sposób naukowy, bez cienia pitagorejskiej mistyki. Wreszcie w dziesiątej księdze zawarty jest wykład o niewymiernościach, będący spadkiem po
Teodorasie z Cyreny i Teratemosie z Aten. Gdyby porównać treść Elementów z tym co wiedzieli w zakresie matematyki poprzednicy Euklides, nie znaleźlibyśmy być może ,w tym dziele nic nowego, tym bardziej, że podobne do Elementów prace istniały wcześniej, chociaż znamy je tylko z tytułów i nazwisk autorów. Do Euklidesa śmiało można odnieść słowa Pascala: "Niech nikt nie twierdzi
,że nie powiedziałem nic nowego;rozmieszczenie treści jest nowe". Bo istotnie, to nowe rozmieszczenie treści olśniewa najbardziej wymagających uczonych do dnia dzisiejszego. W dziele swoim urzeczywistnił Euklides wzór nauki dedukcyjnej, której twierdzenia, jeśli pominąć nieznaczne usterki, wyprowadzane są na drodze czysto logicznej z układu określeń,postulatów i aksjomatów. W
szkole średniej uczymy się następującego twierdzenia Euklidesa: "Pole kwadratu zbudowanego na wysokości trójkąta prostokątnego poprowadzonej z wierzchołka kąta prostego jest równe polu prostokąta o bokach równych odcinkom,na które ta wysokość podzieliła przeciwprostokątną". O autorze Elementów wiemy niewiele i nic pewnego. Pisano wiele o jego dziełach, nic o osobie. Życie jego
przypada na panowanie Ptolemeusza I (323-283),a więc na początek okresu hellenistycznego, w którym wprawdzie rozszerzyły się wpływ kultury greckiej,ale ona sama uległa oddziaływaniu mistycznych prądów Wschodu. Patronowanie nauce przez władców w tym okresie,a zwłaszcza Ptolemeuszów, którzy stworzyli w Aleksandrii sprzyjające warunki dla rozwoju nauki, a między innymi założyli imponującą
bibliotekę,doprowadziło do bujnego rozkwitu nauki i powstania zawodowej grupy uczonych. Poczet wielkich matematyków tej epoki rozpoczyna właśnie Euklides. Oo Proklosa pochodzi niezbyt pewna,lecz charakteryzująca ówczesną atmosferę informacja, według której, Euklides na pytanie Ptolemeusza, czy nie ma prostszej drogi do poznania geometrii niż Elementy,miał dumnie odpowiedzieć ,że w
geometrii nie istnieje osobna droga królewska. Wolno również przypuszczać ,że Euklides pozostawał pod wpływami filozofii platońskiej, jak twierdził Proklos. Przemawia za tym między innymi cecha Elementów - skrupulatne tak charakterystyczne dla Platona i jego zwolenników, omijanie wszelkich zagadnień mających związek z praktyką. W tym samym duchu jest utrzymana informacja Stoajosa:
młodzieniec studiujący geometrię pod kierunkiem Euklidesa miał zadać mistrzowi pytanie,co daje studiowanie geometrii. W odpowiedzi miał się Euklides zwrócić do swego niewolnika ze słowami:"Daj mu trzy obole, ten człowiek chce osiągnąć korzyści z nauki". Powrót
ARCHIMEDES (287-212 p.n.e) : Archimedes urodził się w Syrakuzach w 287 r p.n.e. i tam rozwijał działalność naukową. Początkowe nauki pobierał u swego ojca astronoma Fidiasza;studiował również w Aleksandrii, gdzie nawiązał kontakty z uczniami Euklidesa i utrzymywał już z nimi naukową korespondencję przez całe życie. Część jego dzieł zachowała się.
Wiadomo również ,że Heraklidos napisał jego biografię, która jednak zaginęła. Archimedes jest autorem szeregu niezwykle głębokich i oryginalnych prac głównie z dziedziny matematyki i tym różni się od Euklidesa, który zasłynął raczej jako systematyk przed nim stworzonej wiedzy. Prace Archimedesa dotyczą obliczania pól figur, ograniczonych krzywymi i objętości brył, ograniczonych dowolnymi powierzchniami
,czym wsławił się jako prekursor rachunku całkowego, powstałego w dwa tysiące lat później. Dowód ,że stosunek objętości kuli do objętości opisanego na niej walca wyraża się stosunkiem liczb 2:3, uważał podobno za najważniejsze swoje odkrycie i prosił przyjaciół o umieszczenie tego na nagrobku. Uzyskał najlepsze z dotychczasowych wyniki związane z tradycyjnym problemem kwadratury koła:
1.Pole powierzchni koła jest równe polu trójkąta prostokątnego o przyprostokątnych równych obwodowi i promieniowi koła.
2.Pole koła ma się do pola opisanego na nim kwadratu jak 11:14
3.Stosunek obwodu koła do jego średnicy jest zawarty między liczbami 3 1/7 i 3 10/71.
Wymienione zagadnienia stanowią tylko drobną część twórczości Archimedesa. Dzieła jego są nadzwyczaj trudne; o przystępność nie dbał, pisał stylem oszczędnym, opuszczał łatwe w swoim mniemaniu ogniwa, liczył zapewne na naukową dojrzałość czytelnika. Ci, którzy jak Plutarch, wychwalali jasność wykładu Archimedesa, widocznie żadnej jego książki nie mieli w ręku, natomiast dużej miary matematyk francuski
Franciszek Viete przyznawał ,że nie wszystko zrozumiał. Mimo to wywarł Archimedes ogromny wpływ na rozwój matematyki. Tłumaczyli go gorliwie i komentowali Arabowie, później uczeni zachodnioeuropejscy. Na podstawie zachowywanych licznych informacji biograficznych, których ścisłość jest jednak wątpliwa, można wyrobić sobie pogląd o Archimedesie jako o człowieku i uczonym. W ich świetle przypomina on
poniekąd przysłowiowego "roztargnionego profesora" . Legenda głosi ,że znalazł sposób ustalenia zawartości złota w koronie króla Syrakuz Herona w czasie kąpieli, gdy zauważył ,że woda zaczyna wyciekać gdy wszedł do wanny. Wówczas nago pobiegł do domu z okrzykiem - eureka - znalazłem. Przypisywane mu zdanie : "dajcie mi punkt oparcia a poruszę Ziemię" wiąże się zapewne ze zdarzeniem, gdy na polecenie króla
zbudowana została wspaniała łódź, a robotnicy nie mogli jej spuścić na wodę. Pomógł w tym Archimedes i przy pomocy sporządzonego systemu bloków jeden człowiek, mianowicie sam król, uporał się z tą pracą. Plutarch wysławia Archimedesa za jego udział w obronie rodzinnych Syrakuz przez Rzymianami. Przy pomocy zaprojektowanych przez uczonego katapult oblegani razili wrogów wielkimi głazami i ołowiem, a przy pomocy
żurawi unosili i zatapiali wrogie okręty. Te i podobne podania zdają się świadczyć o zerwaniu z platońską tradycją pełnej izolacji nauki od praktyki, chociaż nie zachowała się , a może nawet nie powstała żadna Archimedesowa praca z zakresu zastosowań matematyki. Zginął w 212 r p.n.e. z rąk rzymskiego żołdaka po upadku miasta, w czasie pracy naukowej. Podobno w ostatnich słowach prosił swego zabójcę aby nie niszczył
rysunku nad którym rozmyślał. W blisko sto lat później Cyceron odnalazł jego grób, który poznał po wyrytej na nagrobku kuli z opisanym na niej walcem. Powrót
APOLLONIUSZ Z PERGI (265(?)-170 p.n.e) : Stulecie od 300 do 200 nosi nazwę wieku Euklidesa. U schyłku tego okresu żył Apolloniusz z Pergi, nazywany przez współczesnych Wielkim Geometrą. Daty jego urodzenia i śmierci nie są ustalone. Najbardziej bujny okres jego twórczości przypada zapewne na ostatnie dziesięciolecie trzeciego wieku. O życiu Apolloniusza niewiele wiadomo.
W młodym zupełnie wieku przybył do Aleksandrii, ówczesnego centrum nauki, uczył się pod kierunkiem uczniów Euklidesa. Z imienia żaden z jego nauczycieli nie był wymieniany. Być może ,że w tym okresie znany był pod przydomkiem Epsilna i zasłynął już z prac w dziedzinie astronomii, które wykorzystał Ptolemeusz. Później pracował w Pergamie, znanym w owym czasie centrum kultury greckiej. Tu zaprzyjaźnił się z Eudemem Permaskim, któremu poświęcił
główne dzieło swojego żywota "Conica" tj. "Stożkowe". Z ośmiu ksiąg cztery zachowały się w języku oryginału, trzy dalsze w tłumaczeniu arabski, ostatnia zaginęła i znana jest tylko z rekonstrukcji dokonanej na podstawie późniejszych komentarzy i znanych siedmiu ksiąg przez E.Halleya (1656-1742). Temat "Stożkowych" nie był nowy. Badaniem figur,powstałych z przecięcia stożka obrotowego płaszczyznami, zajmowali się już Euklides, Archimedes i inni.
Ten fakt skłonił niektórych pisarzy starożytnych,jak na przykład biografa Archimedesa do zarzucenia Apolloniuszowi plagiatu. Na treść stożkowych miały się rzekomo składać nie opublikowane prace Archimedesa. Zarzut ten nie znajduje żadnego uzasadnienia w źródłach historycznych, tym bardziej ,że pojęcia plagiatu i praw autorskich były w owym czasie nieznane i autorzy dość swobodnie korzystali z cudzych prac. Porównanie treści dzieła
Apolloniusza z tym co w przedmiocie stożkowych dokonane zostało do jego czasów, oczyszcza go zupełnie z zarzutu. Poprzednicy Apolloniusza rozważali przecięcia stożków obrotowych płaszczyznami prostopadłymi do tworzących, otrzymując w przypadku stożka prostokątnego parabolę, ostrokątnego - elipsę, rozwartokątnego - gałąź hiperboli. Apolloniusz podszedł do zagadnienia w sposób ogólny, rozważając przecięcie stożków płaszczyznami nachylonymi względem
tworzącej pod dowolnymi kątami, przy czym badania prowadził z drobiazgową dokładnością. W skutek braku ogólnej metody badań stożkowych powstała konieczność rozpatrywania wielu przypadków szczególnych, dlatego też to dzieło się ogromnie rozrosło. W znanych siedmiu księgach znajduje się 387 twierdzeń z dowodami. jest rzeczą zadziwiającą, że autor uporał się z tak wielkim materiałem. Metody geometrii analitycznej, polegające na badaniu tworów
geometrycznych na podstawie ich równań w układzie współrzędnych, pozwalają w prostszy sposób uzyskać wyniki Apolloniusza. te jednak powstały dopiero blisko dwa tysiące lat później , i to pod wpływem jego prac. W siedemnastym wieku odtworzono szereg dzieł Apolloniusza : Viete rozprawkę o styczności, której treścią jest konstrukcja koła stycznego do trzech kół danych, Halley zaś dzieło "O przecięciach przestrzennych". Rekonstrukcją dzieł Apolloniusza
zajmowali się również Fermat, Ghetaldi i Simpson. Heilberg,jeden z najlepszych znawców greckiej matematyki, wspomina o bliżej nie znanym dziele poświęconym podstawą geometrii;z dochowanych szczątków można się domyślać ,że autor usiłował znaleźć pomost między pojęciem matematycznym a rzeczywistością. Byłby to dalszy krok ku oswobodzeniu matematyki z wpływów filozofii platońskiej. Apolloniusz zamyka poczet wielkich twórców w matematyce starożytnej. Nie znaczy
to ,że ustał całkowicie ruch naukowy. Niestety całe niemal piśmiennictwo naukowe z drugiego wieku p.n.e. zaginęło. Nieliczne informacje zawdzięczamy późniejszym komentarzom . Powrót
HERON Z ALEKSANDRII (ok roku 80 p.n.e) : W drugim i trzecim stuleciu p.n.e świat starożytny w wyniku długotrwałych i niszczycielskich wojen dostał się pod panowanie Rzymu. Poziom materialny i kulturalny podbitej ludności, nękanej podatkami i zdzierstwem rzymskich urzędników zaczął stale się obniżać. WIelkie szkoły greckie w Aleksandrii, Pergamonie, Antiochii i Rodosie podupadły, a wraz z nimi również antyczna matematyka.
Rzymianie dla nauki nie wykazywali żadnego zrozumienia i nie wydali w dziedzinie matematyki ani jednego oryginalnego uczonego. Na głęboki upadek myśli matematycznej wpłynął również i charakter tradycyjnej matematyki greckiej z jej czysto geometrycznymi metodami i zupełnym brakiem zrozumienia dla algebry i obliczeń. Ten stan rzeczy uniemożliwił wyjście ku nowym problemom, a stare w ramach stosowanych metod zostały już wyczerpane. Dlatego też u matematyków epoki
rzymskiej, gdy tylko wychodzili poza komentowanie starych tekstów, spotyka się już nowe idee, obce tradycji grecko-paltońskiej, a nawiązujące do dorobku starożytnego Egiptu i Babilonu. Przedstawiciele tej nowej epoki był Heron z Aleksandrii, zwany również Heronem Mechanikiem. Daty jego życia są sporne. Jedni historycy utrzymują ,iż działał on w pierwszym wieku p.n.e, inni natomiast,że w trzecim wieku naszej ery. Warto zauważyć ,iż fakt ,że uczeni nie są w stanie
ustalić daty powstania dzieła w granicach 400 lat, świadczy dostatecznie o skostnieniu i upadku myśli matematycznej. O.Neugebauer, wybitny historyk starożytnej matematyki, opis zaćmienia księżyca zawarty w "Dipotrii" Herona odnosi do 62 roku n.e i przypuszcza ,że sam autor je obserwował. Z przypisywanego mu zbioru matematycznych definicji i komentarza do Euklidesa można się domyślić ,że był nauczycielem. Znał twórczość klasyków greckiej matematyki, sam często ich cytuje, lecz ich
świat abstrakcji nie ma dla niego powabu. Sięga do klasyków, by ich dorobek dopasować do celów praktycznych. Pisał dla inżynierów-praktyków. Głównym jego dziełem jest składająca się z trzech ksiąg "Metrica" (nauka o mierzeniu). Pierwsza księga obejmuje mierzenie powierzchni. Tu podany jest słynny wzór Herona na pole trójkąta wraz z bardzo przejrzystym dowodem oraz różne przykłady liczbowe, wymagające znalezienia pierwiastków kwadratowych z liczb wymiernych,co wykonuje w oparciu o
babilońskie metody przybliżone. Pierwszą księgę kończą rozważania o przybliżonym obliczaniu pól płaskich ograniczonych krzywymi, a także powierzchni "nieprawidłowych". Druga księga obejmuje zagadnienia obliczania objętości i kończy się informacją ,że Archimedes mierzył objętość "nieprawidłowych" brył przez zanurzanie ich w płynie i obliczanie objętości wypartej cieczy. Ostatnia księga zawiera problemy dzielenia figur płaskich i przestrzennych na części pozostające do siebie w danym
stosunku liczbowym. Autor nawiązuje tu do prac Euklidesa, Apolloniusza i Archimedesa, wnosi jednak szereg oryginalnych myśli, podaje również przybliżony sposób obliczania pierwiastków trzeciego stopnia. Heron jest również autorem"Geometrici". Jest ona pod względem treści podobna do "Metrici", lecz wyłożona w zupełnie elementarnej formie. Wzory nie są tu wyprowadzane, lecz ilustrowane licznymi przykładami. Dzieło to nawiązuje do staroegipskiej i starobabliońskiej spuścizny Dobór zagadnień,
używane zwroty i rysunki zdaniem niektórych historyków przypominają papirus Achmesa z około dwóch tysięcy lat p.n.e. Prace Herona z dziedziny mechaniki stosowanej i optyki stawiają go również w rzędzie nauczycieli tych dyscyplin i mają duże znaczenie dla historii nauk przyrodniczych. Osobliwością zachowanej jego rozprawy o pneumatyce jest szereg zawartych w niej pomysłowych "czarodziejskich sztuczek". Heron jest również autorem mechanizmu do automatycznego otwierania drwi świątyń na skutek zapalania
ofiarnego ognia na ołtarzu. Jako matematyk nie był Heron twórczy, dokonał jednak w matematyce doniosłej przemiany: związał ją z potrzebami człowieka i sprowadził ze świata platońskich idei na ziemię . Powrót
DIOFANTOS (koniec III stulecia n.e) : Mnich grecki z XIV wieku, Makysmos Planudes umieścił w swojej antalogii wiersz nagrobkowy, którego treścią jest zadanie algebraiczne. Można z niego obliczyć pewne mało ważne szczegóły biograficzne Diofantosa z Aleksandrii, Żadne inne dane z życia tego wyjątkowego w zasięgu kultury greckiej matematyka nie są znane. Żył, być może,w czwartym wieku n.e., choć pewne fakty przemawiają, iż działalność jego przypada na wiek trzeci.
Diofantos odszedł od tradycyjnych w matematyce greckiej problemów geometrycznych i zajmował się algebrą. Główne jego dzieło "Arytmetyka" , z którego zachowało się sześć ksiąg z prawdopodobnie napisanych trzynastu, zawiera 189 równań wraz z rozwiązaniami. Są to w przeważającej mierze równania nieoznaczone, a więc mające na ogół wiele rozwiązań. Autora interesuje jednak tylko jedno - dodatnie i wymierne. Metod ogólnych nie stosował, sposób rozwiązania zmieniał od zadania do zadania. Wykazywał wiele pomysłowości
w doborze współczynników równań, aby otrzymać żądane rozwiązanie wymierne i dodatnie. Oto przykład diofantoskiego równania wraz z rozwiązaniem. Należy znaleźć dwie takie liczby, których iloczyn zwiększony o każdą z nich jest sześcianem pewnej liczby. Jednej z szukanych liczb autor nadaje postać iloczynu pewnej liczby s przez sześcian liczby 2 tj. 8 s; drugą oznacza przez s2-1 i zauważą ,że pierwszy warunek zadania będzie spełniony jeśli
8s(s2- 1) +8s = (2s)3
Aby był spełniony drugi warunek, wyrażenie
8s(s2-1) + (s2-1)
również musi być sześcianem jakiejś liczby, którą Diofantos oznacza przez 2s-1. Dzięki takiemu doborowi liczb pierwsze równanie sprawdza się tożsamościowo, a w drugim zaś, które jest trzeciego stopnia, znikają wyrazy w trzeciej potędze i natychmiast otrzymuje się rozwiązanie s =14/13. Wśród zadań diofantoskiego zbioru znajduje się szereg pełnych równań stopnia drugiego o jednej niewiadomej, ale autor nie podaje ogólnej metody rozwiązania; jest też jedno w postaci
x3+x = 4x2 + 4
z rozwiązaniem x =4; metody rozwiązania również nie znamy. Być może ,że ogólne metody były treścią zaginionych ksiąg. Rozwiązane równania sprowadzane są do najprostszej postaci,za pomocą kroków, które dziś nazywamy przenoszeniem wyrazów,redukcją wyrazów podobnych i dzieleniem przez współczynnik przy niewiadomej. Diofantos biegle stosuje symbole algebraiczne. Odrębną literą oznacza niewiadomą .Współczynniki pisze za niewiadomą, dla wykładników potęg stosuje oznaczenia będące pierwszymi literami nazw odnośnych liczb w języku greckim;
stosuje oznaczenia dla odwrotności niewiadomej i jej potęg. Znaków dodawania, mnożenia i dzielenia nie stosuje. Składniki sum pisze obok siebie; używa odrębnego znaku dla odejmowania. Ponieważ stosował tylko jeden symbol dla niewiadomej, przeto w zadaniach z wieloma niewiadomymi musiał odpowiednim postępowaniem wszystkie wyrażać przez jedną, wykazując i na tym polu wielką pomysłowość. Stosowane oznaczenia nie stanowią jeszcze współczesnej symboliki algebraicznej, ale można je traktować jako etap pośredni między tzw. algebrą retoryczną a
symboliczną. Przedmiot zainteresowania Difantosa zaliczamy dziś do teorii równań nieoznaczonych. Pewne typy równań nazywamy dziś równaniami Diofantosa. Dzieło jego jednak w świecie starożytnym nie znalazło kontynuatorów. Czerpali z niego w średniowieczu Arabowie, znane było w Indii, lecz pełny obfity plon wydało dopiero w XVII wieku. Powrót
PAPPUS Z ALEKSANDRII (3- 4 stulecie n.e) : W komentarzu do znanego pod arabskim tytułem Almagest dzieła wielkiego astronoma,matematyka i geografa z drugiego wieku n.e. Klaudiusza Ptolemeusza, opisał Pappus zaobserwowane przez siebie w dniu 18 października 320 roku zaćmienie Słońca. Stąd, dzięki przypadkowi,znamy okres, w którym żył. Pracował w Aleksandrii i miał jeszcze do dyspozycji wielką bibliotekę. Wsławił się głównie jako komentator dzieł dawnych matematyków i astronomów,choć bogaty jest jego własny dorobek.
Dzięki Pappusowi znamy autorów, tytuły i fragmenty wielu zaginionych dzieł wybitnych matematyków starożytności. Z licznych jego pism zachował się obszerny traktat "Zbiór matematyczny" . Zawiera on wyciągi dzieł dawniejszych;trudniejsze twierdzenia swoich poprzedników uzupełniał własnymi lematami;cytuje około trzydziestu autorów, dzięki czemu jest on cennym źródłem dla historii matematyki."Zbiór matematyczny" składa się z ośmiu ksiąg. Pierwsza i część drugiej uległy zniszczeniu. Trzecia zawiera historię zagadnień podwojenia sześcianu i trysekcji kąta wraz oryginalnym
rozwiązaniem pierwszego,dalej przykłady konstrukcji trójkątów i równoległoboków o bokach większych od boków danych figur, lecz mniejszej powierzchni, wreszcie nowe konstrukcje pięciu figur foremnych wpisanych w daną kulę. W księdze czwartej znajduje się ciekawe, jak pisze sam Pappus, uogólnienie twierdzenia Pitagorasa następującej treści:
Jeżeli na bokach AB i AC trójkąta ABC zbudujemy dowolne równoległoboki ABDE i ACFG, przedłużymy boki DE i FG do przecięcia ich w punkcie K, połączymy punkty K i A i przeprowadzimy równoległe BH i CJ do KA, to pole otrzymanego równoległoboku BCJH będzie równe sumie pól równoległoboków ABDE i ACFG.
Piąta księga obejmuje zagadnienie figur izometrycznych, czyli posiadających jednakowe obwody. We wstępie do tej księgi ,napisanym pięknym językiem literackim, autor formułując zagadnienie wyraża również panujące wówczas naiwne poglądy filozoficzne. Pisze ,że bogowie obdarzyli człowieka rozumem,zwierzęta zaś instynktem. Tak więc pszczoły nie wydzielają miodu, gdzie popadnie, lecz zebrawszy aromat z najpiękniejszych kwiatów budują najpierw naczynia, wszystkie równe, wzajemnie przylegające. Jednakże tylko try foremne figury:trójkąt, kwadrat i sześciokąt spełniają te warunki.
Pszczoły obrały dla tych naczyń tę figurę ,która ma najwięcej kątów, gdyż wywnioskowały,że one mieszczą więcej miodu niż pozostałe przy jednakowym zużyciu materiału. My zaś mający większe pretensje do rozumu niż pszczoły,zajmujemy się ogólniejszymi zadaniem okazania, że ze wszystkich płaskich figur o równym obwodzie największą powierzchnię ma , ta która posiada największą liczbę kątów, a ze wszystkich płaskich figur o równym obwodzie największą powierzchnię ma koło... Zauważa też ,że filozofowie utrzymywali ,iż świat ma kształt kuli, "najwspanialszego"
i największego z ciał o równej powierzchni, lecz nie dowiedli ,że kula ma większą objętość niż każdy z foremnych wielościanów o równej powierzchni. Szósta księga zawiera problemy astronomiczne związane z geometrią. Szczególnie ważna z punktu widzenia historycznego jest księga siódma. Autor zajmuje się w niej m.in. analizą i syntezą starożytnych, ilustrując stosowane metody licznymi przykładami z zaginionych dzieł starożytnych matematyków. Ostatnia księga traktuje zagadnienia z mechaniki. Pappus jest ostatnim geometrą greckim. Po nim Aleksandria nie wydała już większych twórców
lecz tylko komentatorów. Wśród komentatorów poczesne miejsce zajmuje Hypatia, bohaterka wielu powieści, filozof, matematyk, astronom i lekarz. Spod jej pióra wyszły zaginione komentarze do dzieł Diofantosa i Apolloniusza. Była profesorem platońskiej filozofii w Aleksandrii, gdzie też miała szerokie stosunki w najwyższych sferach. Późniejszy biskup Synescos nazywał ją "matką, siostrą i szanowaną nauczycielką". Mimo to jako poganka ,padła ofiarą fanatyzmu chrześcijan. Została zlikwidowana także słynna uczelnia aleksandryjska, która była placówką pogańskiej kultury hellenistycznej.
Jeszcze przez jakiś czas działała platońska Akademia w Atenach, skąd wyszedł Proklos, autor komentarzy do Euklidesa oraz Eudemos, któremu zawdzięczamy pewne informacje o pracach Hipokratesa. Ale i ta szkoła, ostatnia placówka pogaństwa, została w 529 roku z rozkazu cesarza Justyniana zamknięta. Powrót
ERAZM WITELO (1220(?) - 1270(?)) : Ciekawą,niemal legendarną postacią jest Witelo (Witeliusz, Witelo). Jest to pierwszy matematyk i w ogóle uczony,jaki urodził się na polskich ziemiach. Urodził się prawdopodobnie między rokiem 1220-1230 pod Wrocławiem. Był synem Polki i niemieckiego kolonisty- Turynga, który osiedlił się w Polsce za Bolesława Wstydliwego. Witelo kształcił się na uniwersytetach zagranicznych. Około roku 1253 studiował w Paryżu. Po powrocie na Śląsk przez klika lat pracował jako nauczyciel przypuszczalnie w szkole legnickiej.
W latach 1262-1268 przebywał w Padwie, gdzie studiował prawo kanoniczne oraz filozofię i nauki ścisłe. W liście pisanym z Padwy nazywa się siebie "Vitelo Plebanus" - stąd pewne przypuszczenie ,że miał zamiar zostać duchownym. Około roku 1269 nawiązuje kontakt ze spowiednikiem papieskim i wyjeżdża do Rzymu,gdzie przebywa na dworze papieża Klemensa IV. Tu interesuje się matematyką. Wiadomości jakie zachowały się o Witelonie są skąpe, pełne domysłów i sprzeczności, trudnych często do sprawdzenia. Na przykład w 1810 roku profesor Uniwersytetu Jagielońskiego Józef Sołtykiewicz wyraził przypuszczenie,
że imię Witelona powstało przez latynizację jego właściwego nazwiska Ciołek (łac. Vitellus), Mniemanie to tak się rozpowszechniło, że zostało nawet zanotowane w różnych encyklopediach, mimo iż nie ma pewnych na to dowodów. Trudne jest także do sprawdzenia (choć są pewne przypuszczenia) ,czy Witleo po ukończeniu studiów wrócił kiedykolwiek do Polski. Można by stąd wyciągnąć wniosek ,że związek Witelona z Polską jest dość luźny. Jednakże sam Witleo uważał się z Polaka, o czym wyraźnie mówi w X księdze "Optyki": "W naszej ziemi,mianowicie Polsce, w tej ,która jest zamieszkana pod 50 stopnie szerokości".
Nie wiadomo także dokładnie, gdzie zmarł Witelo, jego śmierć nastąpiła prawdopodobnie około 1270 roku. W czasie pobytu w Rzymie napisał Witelo po łacinie dwa dzieła, z których pierwsze : "Wnioski z Elementów Euklidesa",zawierające wszystkie twierdzenia geometryczne odkryte po Euklidesie, niestety zaginęło. Drugie jego dzieło - to traktat o optyce w dziesięciu księgach,pod pełnym tytułem:"Witelona matematyka uczonego o optyce, to jest o istocie, przyczynie i padaniu promieni wzroku, światła, barw oraz kształtów, którą powszechnie nazywają perspektywą, ksiąg dziesięcioro". Dzieło to wyszło w Bazylei w 1272 roku.
I księga tego dzieła zawiera twierdzenia i dowody matematyczne (także oryginalne twierdzenia Witelona), które stosuje potem w swoich rozważaniach optycznych. Dzieło to odegrało w dziejach nauki dużą rolę, ukazało się w wielu kopiach i wydaniach, często pod krótkim tytułem "Optyka" lub "Perspectiva". Ciekawe jest ,że choć nie zawierało ono istotnie nowych pomysłów, było podstawową pracą w dziedzinie optyki - było podręcznikiem, z którego korzystało wielu tak wybitnych uczonych jak Kopernik, Kepler, Regiomontanus. W 400 lat później, Kepler zatytułował skronie jeden ze swoich traktatów o optyce"Ad Vitellonem Paralipomena"
czyli "Dopełnienie Witelona". Mimo iż osiągnięcia Witelona w zakresie matematyki są mniejsze niż w optyce, zasługują na uwagę. Witelo był jednym z nielicznych uczonych swego stulecia zajmujących się krzywymi stopnia drugiego i wyższych, dla kreślenia niektórych skonstruował nawet odpowiednie przyrządy. Znał także bardzo dobrze trygonometrię i stosował ją w badaniach optycznych .Zwróćmy uwagę ,że okres jego działalności przypada na drugą połowę XIII wieku, gdy w szkołach polskich zadaniem matematyki było jedynie przygotowanie do zrozumienia kalendarza i podstawowych zjawisk zachodzących na niebie. Dopiero na wyższych
szczeblach nauczania uczono bez dowodów na pamięć ważniejszych twierdzeń z "Elementów" Euklidesa. Ponieważ Witelo swe doświadczenia z dziedziny optyki przeprowadzał na górze Lasota, przy mogile Krakusa, niektórzy historycy twierdzą,że od tego czasu wzrosła liczba podań o Twardowskim. Powrót
WOJCIECH BLAR Z BRUDZEWA [BRUDZEWSKI] (1445-1487) : Historia nauki polskiej okresu średniowiecza to zarazem historia krakowskiej Alma Mater. Jako jedyna podówczas wyższa uczelnia w Polsce, była Akademia Krakowska, siłą rzeczy, kulturalnym i naukowym ogniskiem kraj. Tutaj otrzymał swe wykształcenie Kopernik, tutaj wykładał znakomitemu Polakowi matematykę i astronomię słynny Wojciech Blar z Brudzewa. W przeciwieństwie do swego ucznia Wojciech Brudzewski dość wcześnie zyskał sobie sławę jako astronom i matematyk, później zaś jako teolog. Wspomagany możną protekcją władców polskich
i łaską wszechwładnego kościoła, łatwiejsze też miał życie. Urodził się we wsi Brudzewo koło Sandomierza w roku 1445 i swe młodzieńcze nauki pobierał w Opocznie, potem zaś w Akademii Krakowskiej. Wykładali mu tutaj znani profesorowie: matematyki Jan z Głogowa, fizyki Michał z Wrocławia. Swój pierwszy stopień naukowy - bakałarza ("laura prima") uzyskał Wojciech w 1470 roku, stopień zaś doktora ("laura secunda") w roku 1474. Kolejne awanse dają mu w końcu wykłady matematyki i filozofii, a także teologii, które ugruntowują jego sławę, ściągając do Krakowa wielu cudzoziemców pragnących ich wysłuchać. Jego wiedza, osobisty urok, prócz tego
snobizm magnata pragnącego mieć na dworze znanego uczonego, sprawiają ,że Wojciech opuszcza w 1494 uczelnię krakowską i udaje się do Wilna na dwór Wielkiego Księcia Litewskiego Aleksandra. Radość możnowładcy wszakże nie trwała długo. Trudno ustalić,co zaszkodziło Wojciechowi, czy to nadmiar łaski, czy też zmiana klimatu. Dość ,że po trzech latach pobytu u księcia Brudzewski umiera mając lat 52. Z jego prac naukowych wymienić należy, zalecane w swoim czasie jako najlepsze w swym rodzaju, wydane w Mediolanie, komentarze do współczesnej mu teorii planet "Commentaria utilissima in theoreticis planetarum in studico generali Cracoviensi;per Albertum
de Brudzewo, pro introductione juniorum corrogatum,impressum Mediolani, alte Ulderici Scinzenzelor" (1495) i opis użycia i konstrukcji przyrządu stosowanego w astronomii i żegludze: "De Constructione Astrolabii". Ponadto Wojciech z Brudzewa układał kalendarze całoroczne opatrzone podstawowymi wiadomościami i wskazówkami astronomicznymi. Za miarę trzeźwości i światłości tego umysłu może posłużyć stanowczość, z jaką przeciwstawiał się Wojciech powszechnym i modnym wówczas, jednocześnie mętnym rozważaniom astrologicznym. Powrót
MIKOŁAJ KOPERNIK(1473-1543) : Wielu ludziopm nazwisko Kopernika nie kojarzy się z matematyką. Wydaje się im ono związane przede wszystkim z astronomią. Na pewno zaś przypomina im się wtedy, gdy stają się śwaidkami przełomowych wydarzeń w życiu ludzkiej społeczności. W ich rozumieniu Koppernik jest symbolem postępu, symbolem śmiałej zmieniającej ludzki obraz świata rewolucyjnej myśli. Ale rzecz jasna, mógł się nim stać właśnie dzięki swym odkryciom naukowym, głównie astronomicznym. Nie należy jednak zapominać ,że każdy ówczesny, piętnastowieczny astronom, to także matematyk, lekarz - słowem uczony.
Kopernik był człowiekiem swojej epoki, epoki której dał nazwę. Znane są szeroko osiągnięcia Kopernika - astronoma. One zapewniły mu przede wszystkim nieśmiertelną sławę. Ale znamy także Kopernika-matematyka, inżyniera, lekarza. Interesujący nasz Kopernik -matematyk napisał wszakże tylko jedną pracę czysto matematyczną - "Trygonometrię" ,ale rozważania dotyczące innych dziedzin matematyki - geometrii, algebry zamieścił w swych głównych pracach astronomicznych, w których wyniki obu tych gałęzi wiedzy wzajemnie się przeplatają i uzupełniają. Genialny Polak urodził się w Toruniu w 1473 roku. Mikołaj był najmłodszym wśród swego rodzeństwa. Po śmierci ojca
młodym Kopernikiem zaopiekował się jego wuj Łukasz Waczenrode, od 1489 roku biskup warmiński. Swą edukację rozpoczął Kopernik w Toruniu, kontynuował zaś w Chełmnie. W 1491 roku zapisuje się w poczet uczniów Akademii Krakowskiej. Tutaj studiuje przez trzy lata nauki humanistyczne i przyrodnicze, będąc uczniem Wojciecha z Brudzewa. W 1494 roku Kopernik wstępuje do stanu duchownego i w dwa lata później udaje się do Włoch, do Bolonii, gdzie rozpoczyna studia prawnicze, nie zaniedbując także matematycznych. w międzyczasie uzyskuje godność kanonika we Fromborku,zapewniając sobie materialną niezależność. W ciągu studiów we Włoszech uzyskuje w Ferrarze doktorat prawa i
kończy medycynę. Wreszcie w roku 1503 powraca do kraju i osiada na stałe we Fromborku. Koncepcje astronomiczne Kopernika dotyczące ruchu Słońca, Ziemi i pozostałych planet nasunęły mu się dość wcześnie. Ich ślady sięgają do 1509 roku, gdzie znajdujemy je w dokonanym przez Kopernika przekładzie z greki na łacinę listów pisarza bizantyjskiego Symokatty. Niemniej dopiero w 1512 roku napotykamy pierwsze wyraźne sformułowanie poglądu. Od tego czasu Kopernik usilnie rozwija swoją hipotezę, popierając ją obliczeniami i obserwacjami. Jednocześnie wiedzę którą posiadał, usiłował oddać dla dobra kraju. Tak więc w 1526 roku w związku z inflacją pieniądza Kopernik na zlecenie
króla opracowuje "Rozprawę o urządzeniu monety", dając konkretne propozycje poprawy sytuacji monetarnej w kraju. Jego działalność we Fromborku jako lekarza i jednego z gospodarzy miasta jest dobrze znana. Jemu przypisuje się zaprojektowanie i założenie wodociągów w mieście. Heliocentryczna teoria ruchu planet, będąca zasadniczym dziełem życia Kopernika, wolno zyskiwała rozgłos, ale była znana już ludziom za życia uczonego. W końcu zainteresowanie nią było tak wielkie, że w 1536 roku kardynał M.Schonberg pisał do Kopernika :"Dlatego, męzu głęboko uczony, jeżeli Ci nie będę natrętnym, proszę Cię i błagam jak najusilniej, ażebyś całe to swoje odkrycie miłośnikom nauki zakomunikował.." .
Biskup warmiński Gize, darzący przyjaźnią Kopernika, pisał o nim do Erazma Z Rotterdamu i do Jerzego Rhetika, słynnego wówczas w Niemczech profesora matematyki. Ten oststni z polecenia uczonych niemieckich udał się w roku 1538 do Fromborka. Przyjęty serdecznie przez Kopernika, zajął się streszczeniem i wydaniem jego dzieła. Wkrótce po powrocie Rhetika do Wittembergii ukazała się drukiem treść trzech pierwszych ksiąg Kopernika, opatrzona tytułem "Narratio de libris revolutionum Copernici" (w Gdańsku 1540 roku). Drugie jej wydanie wyszło niebawem w Bazylei. W dwa lata potem w Wittemberdze ukazała się "Trygonometria" Kopernika. Wreszcie w 1543 roku, jużu schyłku życia Kopernika, wyszło na
świat główne dzieło, znamionujące początek nowej epoki : "De revolutionibus orbium coelestium" ("O obrotach sfer niebieskich")."Trygonometria" zawarta jest w ksziędze I dzieła w rozdziałach XII,XIII i XIV. Rozdział XII traktuje o cięciwach koła, rozdział XIII - o bokach i kątach trójkątów płaskich, rozdział XIV - o trójkątach kulistych. W swym wykładzie Kopernik trzymał się dość ściśle "Almagestu" Ptolemeusza, a także wzoruje się na trygonometrii sferycznej Gebera Sewilskiego, znanego Kopernikowi ze studiów w Krakowie. Jednakże rozwiązanie dwóch najdonioślejszych zadań dotyczących trójkątów sferycznych, a mianowicie "mając dane trzy boki ,znaleźć kąty" i "mając dane trzy kąty, z których żaden
nie jest prosty, znaleźć boki" należy przypisać samemu Kopernikowi. Grupując główną treść matematyczną dzieła rozdziały powyższe nie są przecież jedynymi, które je zawierają. Tak np. rozdział IV księgi III zawiera dowód twierdzenia : "Jeżeli o wewnętrznej stronie danego koła toczy się ,bez poślizgu koło o średnicy równej promieniowi danego koła, to każdy punkt na obwodzie koła mniejszego zakreśla linię prostą - jedną ze średnic koła większego". W swej teorii precesji w rozdziale III księgi III Kopernik rozważa krzywą w kształcie ósemki; jest to krzywa algebraiczna czwartego stopnia - jedna z tzw. figur Lissajnosa. Ustęp VII księgi VI zawiera natomiast zasadę stosowania średniej arytmetycznej
przy opracowaniu rezultatu szeregu pomiarów. Kopernik nie był matematykiem w dzisiejszym rozumieniu tego słowa. Traktował matematykę raczej jako narzędzie w swych wysiłkach przebudowy wyobrażeń o Wszechświecie. Niemniej na marginesie tych wysiłków pozostawił z tej dziedziny prace, które mają dla każdego matematyka niezapomnianą , historyczną wartość. Powrót
GERONIMO CARDANO(1501-1576) :Odkąd środek ciężkości nauki włoskiej XV i XVI wieku przeniósł się do północnych miast Italii: do Genui, Pizy, Wenecji, Mediolanu i Bolonii, będącymi wówczas handlowymi ośrodkami Włoch, odtąd można było zanotować w historii matematyki nowe fakty, które pozwoliły wreszcie wyjść jej z dość ciasnego kręgu zainteresowań podzielanych przez starożytnych Greków i Arabów. Fakty te stworzyli włoscy matematycy uniwersytetu bolońskiego, który właśnie w XVI wieku stał się jednym z największych i najsławniejszych w Europie. W ich liczbie znaleźli się :Scipion del Ferro,Nicolo Tartaglia i Hieronim Cardano. Na owe fakty złożyły się wyniki
badań nad rozwiązaniem sześciennego równania algebraicznego. Wbrew pesymistycznym ocenom udało się w końcu del Ferro znaleźć rozwiązanie ogólne tego równania, ponownie otrzymanego przez Trataglię. Obaj jednak nie opublikowali swoich wyników. Uczynił to dopiero lekarz, fizyk i matematyk Hieronim Cardano. Cardano urodził się w 1501 roku w Padwie, gdzie jego ojciec Bonifacy był znanym lekarzem i prawnikiem. Do dwudziestego roku życia Hieronim kształcił się pod okiem ojca,po czym rozpoczął studia na uniwersytetach Pawii i Padwy. W tej ostatniej uczelni w roku 1524 otrzymuje tytuł doktora medycyny. Cardano zdobył najwcześniej sławę jako lekarz. Sięgała ona aż do Anglii, do której udał się w podróż, by leczyć
tam szkockiego prymasa Hamiltona. Od roku 1534 uczony ten wykładał w Mediolanie matematykę i nauczał medycyny. W jedenaście lat potem wydaje on zasadniczą swoją pracę z matematyki, zatytułowaną "Artis magnae sive de regulis akgebraicis". Pomieścił w niej jakoby rozwiązania Tartaglii równania sześciennego, co doprowadziło do publicznej kłótni, w której obie strony nie szczędziły sobie obelg. Ponadto praca podawała, znalezioną przez ucznia Cardana - Ludovico Ferrari, metodę sprawdzania równania stopnia czwartego do równania sześciennego. Tej właśnie pracy zawdzięcza swą pozycję w historii matematyki. Jednakże nie należała ona do jedynych. Jego "Liber de ludo aleae", książka zajmująca się grami hazardowymi,
przedstawia pierwsze systematyczne obliczenia prawdopodobieństw, i to na wiek przed Pascalem i Fermatem! Poza tym Cardano publikował prace o tematyce fizycznej i filozoficznej. Najbardziej znaną z nich była "De subtilitae rerum", która będąc zbiorem doświadczeń fizycznych i przeplatana anegdotami cieszył się ogromnym powodzeniem. Późniejsze życie Cardano było tragiczne. Już w 1546 roku umiera mu żona. Najbardziej jednak bolesna strata oczekuje Cardana w 1560 roku, kiedy to za otrucie swojej żony zostaje ścięty jego 26-letni syn Jan, także lekarz .W końcu posądzony o herezję zostaje Cardano w 1570 roku aresztowany. Chociaż uwolni się z zarzutów i wyjdzie na wolność, to nie będzie mógł już odzyskać w życiu
utraconych pozycji. Cardano po ukończeniu autobiografii "De proprie vita" umiera w Rzymie w 1576 roku. Powrót
FRANCOIS VIETE(1540-1603) : Chociaż Viete (Vieta) był prawnikiem z wykształcenia i z zawodu, zdradzał zamiłowanie i talent do nauk ścisłych. JUż jako młody oficer królewski oddał Francji niezwykłą przysługę. Udało mu się mianowicie na drodze dedukcji matematycznej znaleźć klucz do szyfru, którym posługiwał się król Hiszpanii Filip II. Dzięki temu udostępnił Francuzom wszystkie ściśle tajne wiadomości króla hiszpańskiego. Szyfr ten składał się z ponad 500 symboli. Filip II był pewien ,że nikt nie potrafi go rozszyfrować. dlatego też gdy odkrył ,iż Francuzi potrafią czytać jego listy, wniósł skargę do papieża o użycie czarów przeciwko niemu. Francois Viete urodził się
w 1540 r. w Poiton koło Fonteney-le-Comte. Po ukończeniu prawa został adwokatem w swoim rodzinnym mieście. Po wstąpieniu na tron Henryka IV zostaje w 1589 roku radcą Parlamentu w Tours,a później pierwszym radcą królewskim. Zainteresowawszy się astronomią, Viete zmuszony był zająć się trygonometrią i algebrą. Wprawdzie do czasów Vietea w dziedzinie algebry nastąpił już pewien rozwój symboliki oraz znane były rozwiązania równań trzeciego i czwartego stopnia przez pierwiastkowanie, lecz dopiero on swoimi pracami dał podstawy ogólnej nauce o równaniach algebraicznych, zyskując tym miano ojca współczesnej algebry. Jako pierwszy wprowadził literowe oznaczenie nie tylko do dla wielkości niewiadomych (co niekiedy stosowano wcześniej)
ale i dla wielkości danych, to jest dla współczynników. W ten sposób dopiero dzięki niemu otwarła się możliwość wyrażania równań i ich pierwiastków ogólnymi wzorami. Viete podał ogólne metody rozwiązywania równań drugiego,trzeciego i czwartego stopnia, ujednolicając tym samym metody podane wcześniej przez Ferro i Ferrariego oraz wprowadził znane każdemu uczniowi wzory na sumę i iloczyn pierwiastków równania kwadratowego (wzory Vietea). Wszystkie te osiągnięcia zawarł w napisanej w 1591 roku pracy "Isagoge in artem analiticam". Drugie jego dzieło "Recensio canonica effectionum geometricarum" jest natomiast podstawą dziedziną matematyki zwanej dziś geometrią analityczną. W trygonometrii podał pełne rozwiązania zadnia o obliczaniu wszystkich elementów
płaskiego i sferycznego trójkąta, gdy trzy elementy są dane. Znalazł również bardzo ważne rozwiązanie na szereg wielkości cos nx i sin nx według potęg cos x i sinx. Również jako pierwszy rozpatrzył iloczyn nieskończony. Viete wydawał na swój koszt bardzo wiele prac świadczących o jego wieloletnich zainteresowaniach i rozsyłał je do uczelni prawie wszystkich krajów europejskich. Prace te jednak były pisane bardzo trudnym językiem i dlatego nie rozpowszechniły się w takim stopniu, na jaki zasługiwały. W przeszło 40 lat po śmierci Francois Viete dziełą jego zostały wydane przez F. van Schootena pod wspólnym tytułem : "Opera Mathematica". Powrót
JAN BROŻEK [BROSCIUS](1585-1652) : Wybitny polski matematyk XVII w .urodził się 1 listopada 1585 roku w miasteczku Kurzelów w ziemi sieradzkiej. Ojciec jego, aczkolwiek rolnik, nauczył go czytać i pisać, a także dał mu początki geometrii. Dalszą naukę pobierał Brożek w szkole kolegialnej w Kurzelowie. W 1604 roku rozpoczął studia na wydziale filozoficznym Uniwersytetu Krakowskiego. Tutaj zajmuje się szczególnie matematyką i astronomią, która w owym czasie ściśle łączyła się z astrologią. w 1605 roku uzyskuje już stopień bakałarza nauk wyzwolonych, a w 1610 roku magistra sztuk wyzwolonych i tytuł doktora filozofii. Ogłasza jednocześnie w języku łacińskim pierwszą rozprawę matematyczną pt
"Geodezja odległości bez przyrządów i miejsce nieco niejasne u Polibiusza geometrycznie wyjaśnione przez Jana Brożka". W pracy tej podaje metodę obliczania odległości dwu punktów, z których jeden jest niedostępny .W pracy tej wykazał ,że jeżeli koło, kwadrat i trójkąt równoboczny mają ten sam obwód, to największą powierzchnię ma koło a najmniejszą trójkąt równoboczny. W 1611 roku wydaje Brożek następną swoją pracę "Problem geometryczny , w którym wykazuje się na podstawie geometrii prawdziwą i istotną praprzyczynę, dlaczego pszczoły budują plastry w formie sześciokątnych komórek". Zagadnienie, choć nie nowe,rozwiązał Brożek w sposób oryginalny. Zauważył bowiem, że aby pokryć płaszczyznę wielokątami foremnymi, należy zestawić przy jednym wierzchołku
albo sześć trójkątów równobocznych, albo cztery kwadraty,a lbo też trzy sześciokąty foremne. Ponieważ przy tych samych obwodach sześciokąt ma największą powierzchnię, przeto komórka sześciokątna ma największa objętość przy najmniejszym zużyciu materiału. W tymże roku Brożek przyjmuje niższe święcenia kapłańskie. W 1614 roku zostaje powołany na stanowisko astrologa zwyczajnego,który to urząd pełni przez 15 lat. jakkolwiek Brożek z racji swych obowiązków zajmował się układaniem horoskopów, nie wydaje się ,aby przywiązywał do nich większą wagę. W opublikowanej w 1616 roku pracy "Czy geometrzy więcej aniżeli astronomowie pomagają sprawom publicznym" podaje szereg zastosowań praktycznych geometrii i wyraża pogląd, ze astronomia wywodzi się z geometrii, to znaczy-
jest geometrią nieba. Brożek zajmował się również praktycznie pracami geodezyjnymi, między innymi sporządził plany kopalni w Wieliczce i Bochni. Warto również wspomnieć ,że Brożek zbierał dokumenty dotyczące życia i pracy Mikołaja Kopernika, które niestety zaginęły. W 1619 roku po publicznej obronie pracy habilitacyjnej zostaje profesorem Akademii. W 1620 roku wydaje książkę "Arytmetyka liczb całkowitych". Obszerne to dzieło składa się z szesnastu rozdziałów i obejmuje materiał do działań na liczbach całkowitych do nauki logarytmów. w tymże roku Brożek wyjeżdża do Padwy na studia medyczne. Po czteroletniej nauce powraca jako doktor medycyny do Krakowa gdzie nadal zajmuje się matematyką. Jako lekarz nie praktykował prawie wcale. W 1625 roku, w czasie zatargu
między Akademią a zakonem jezuitów o zwierzchnictwo nad otwartym kolegium jezuickim, Brożek ogłasza anonimowo satyrę w trzech częściach pt. "Dyskurs ziemianina z plebanem". Satyra ta świetnie napisana do dziś jest perełką literatury polemicznej tego okresu. W 1629 roku przyjmuje Brożek pełnie święcenia kapłańskie i przechodzi do Wydziału Teologicznego Akademii. Nieco później ogłasza w języku polskim pracę pt. "Przydatek pierwszy do Geometrii Polskiej Stanisława Grzepskiego". W latach następnych zajmuje się sprawami Akademii,często podróżuje. Warto wspomnieć ,że w dowód uznania dla jego osiągnięć naukowych ofiarowano mu w 1632 roku dwa probostwa w Staszowie i Międzyrzeczu, gdzie przez dłuższy czas mieszkał. W 1637 roku wydaje rozprawę o liczbach doskonałych i
zaprzyjaźnionych, a w roku 1638 "Obronę Arystotelesa i Euklidesa przeciw Piotrowi Ramusowi". W pracy tej podaje kilka nowych twierdzeń z zakresu geometrii, wzbogacając ją zarazem nowymi metodami w dziele wielokątów gwiaździstych. Do roku 1648 Brożek przebywa na wsi,skąd po powrocie w 1649 r. zostaje ponownie przyjęty do Collegium Majus Akademii. Wkrótce zostaje promowany na doktora teologii (1650r.),a w dwa lata później zostaje dziekanem Wydziału Teologicznego. W tym samym roku Brożek zostaje wybrany rektorem Akademii, jednak urząd ten piastuje tylko pięć miesięcy, bowiem 21 listopada 1652 roku umiera. O oddaniu Brożka sprawom nauki najlepiej chyba świadczy fakt ,że w testamencie cały swój niemały dobytek zapisał Akademii, część zaś funduszów przeznaczył na
rozwój szkoły w Kurzelowie i na otwarcie scholasterii, o której zorganizowaniu myślał jeszcze za życia. Powrót
RENE DESCARTES [KARTEZJUSZ](1596-1650) : Rene Descarte jest właściwie bardziej znany jako wielki filozof niż matematyk. Niemniej był pionierem nowoczesnej matematyki i zasługi jego w tej dziedzinie są tak znaczne ,że nie sposób go pominąć. O życiu Kartezjusza nie wiemy jednak zbyt wiele. Urodził się we Francji, w małym miasteczku La Haye w Touraine. Po ukończeniu jezuickiego kolegium dla arystokratów studiował idąc śladami swojego brata, prawo. Mając 22 lata opuszcza Francję i służy jako oficer - ochotnik w wojskach różnych europejskich wodzów, biorących udział w wojnie trzydziestoletniej. W ten sposób przemierza Węgry, Czechosłowację i Austrię. Kartezjusz głosił racjonalistyczne idee o potędze rozumu ludzkiego i z tego
względu spotkał się z prześladowaniami ze strony kościoła katolickiego. Dlatego też, chcąc znaleźć warunki umożliwiające mu pracę naukową (a jego zainteresowania filozofią i matematyką datują się od czasów szkolnych)osiedlił się w 1629 roku w Holandii, gdzie spędził prawie całą resztę swojego życia. W jednym ze swych listów Kartezjusz wyraża w następujący sposób swoje zadowolenie z pobytu w Holandii:"Tu każdy oprócz mnie jest tak zajęty swymi interesami i dochodami,że mógłbym przeżyć całe życie , nie będąc zauważonym przez kogokolwiek... W którym innym kraju można cieszyć się taką wolnością, gdzież można by spać z większym spokojem niż tu ,gdzie trucizna, zdrada, oszczerstwo są znacznie mniej znane". W Holandii Kartezjusz napisał wszystkie swoje wielkie prace w dziedzinie
filozofii,matematyki, fizyki, kosmologii i fizjologii. Swój dorobek w dziedzinie matematyki zebrał w jednym dziele "Geometria" (1637). Przedstawił w nim podstawy geometrii analitycznej i algebry. Po raz pierwszy wprowadził pojęcia: zmiennej, funkcji oraz współrzędnych prostokątnych, które do dziś nazywamy współrzędnymi kartezjańskimi. Linie krzywe dające opisać się równaniami algebraicznymi podzielił na klasy, w zależności od najwyższej potęgi zmiennej występującej w równaniu. Wprowadził znak "+" i "-" dla oznaczenia liczb dodatnich i ujemnych,oznaczenie potęgi (x*x=x2) oraz symbol nieskończoności. W oparciu o dorobek Kartezjusza rozwinął się później (dzięki Newtonowi i Leibnizowi)rachunek różniczkowy. Kartezjusz umarł w Sztokholmie, spędziwszy tam ostatni rok swego życia.
Chociaż nie posunął się daleko w dziedzinie geometrii analitycznej, jednakże dzieło jego wywarło decydujący wpływ na dalszy rozwój matematyki. W ciągu 150 lat algebra i geometria analityczna rozwijały się w kierunku wskazanym przez niego. Powrót
PIERRE FERMAT(1601-1665) : Piotr Fermat, prawnik i matematyk francuski, urodził się w Beaumont de Lomange pod Beaumont w 1601 roku. Pochodził z mieszczańskiej rodziny. Studiował na uniwersytecie w Tuluzie,gdzie ukończył wydział prawa, a następnie od roku 1631 do końca życia był radcą prawnym parlamentu w tym mieście. Chociaż matematyce poświęcał tylko czas wolny od zajęć, znał jednak doskonale nie tylko matematykę współczesną ale i starożytną. Wsławił się pracami w zakresie teorii liczb. W 1638 odkrył metodę znajdowania maksimów i minimów funkcji algebraicznych. Uważany był za jednego z poprzedników Newtona i Leibniza w dziedzinie rachunku różniczkowego i całkowego. Powszechnie za twórcę geometrii analitycznej, której metoda polega na wprowadzeniu
układu współrzędnych i zastosowaniu algebraicznych równań do badania własności figur geometrycznych, uważa się Rene Descartesa. Tymczasem okazuje się ,że już w 1636 Fermat w swej pracy,której nie wydał drukiem, gdyż nie lubił tego czynić, wprowadził metodę prostokątnego układu współrzędnych,wykazał on,że równaniom pierwszego stopnia odpowiadają proste, a równaniom drugiego stopnia :elipsy,hiperbole, parabole i inne linie,które można otrzymać z przecięcia stożka płaszczyzną (tzw. stożkowe). W celu ułatwienia badań równań algebraicznych I i II stopnia Fermat stosował przesunięcie i obrót układu współrzędnych,co pozwalało mu na otrzymanie najprostszych tzw. kanonicznych postaci równań linii, z których wysnuwał geometryczne właściwości. Rozwiązania w dziedzinie geometrii analitycznej powstały wskutek zainteresowań
Fermata pracami starożytnych matematyków, w szczególności Apoloniusza o miejscach geometrycznych. W 1621 r. zostały przetłumaczone na język łaciński prace Diofantosa,jednego ze starożytnych twórców teorii liczb. Fermat traktował czytanie książek matematycznych za pewnego rodzaju rozrywkę i miał zwyczaj pisania swych spostrzeżeń na marginesach. Podał w ten sposób wiele własnych twierdzeń, nie troszcząc się o ich dowód. Tak powstało słynne wielkie twierdzenie Fermata, które nabrało ogromnego rozgłosu. Dotyczy ono liczb pitagorejskich (3,4,5);(6,8,10);(9,12,25); itd, spełniających równanie a2+b2=c2. Fermat postawił zagadnienie, czy można znaleźć takie liczby naturalne a,b,c, aby dla liczb naturalnych n > 2 zachodziła równość an+bn=cn. Otóż na
marginesie jednej z książek Fermat napisał, że powyższe twierdzenie nie ma rozwiązań w liczbach całkowitych przy żadnym n > 2 i ,że ma zadziwiający dowód tego twierdzenia ,ale zbyt długi na to ,aby zmieścił się na marginesie. Gdy po śmierci Fermata jego syn opublikował w roku 1670 notatki i listy ojca, wielu matematyków usiłowało dać dowód twierdzenia, ale bezskutecznie. Zmarły w 1907 roku w Darmstadcie lekarz i matematyk Paweł Wolfskehl zapisał Królewskiej Akademii Nauk w Getyndze 100 000 marek z poleceniem rozpisania konkursu na wynalezienie dowodu wielkiego twierdzenia Fermata.W między czasie na skutek dewaluacji marki niemieckiej wartość nagrody zmalała niemal do zera. W 1994 roku dowót tego twierdzenia ogłosił angielski matematyk Andrew Wiles. Słynne jest też małe twierdzenie Fermata,które głosi ,że jeśli p jest
liczbą pierwszą, nie będącą podzielnikiem liczby a, to ap-1 po podzieleniu przez p daje resztę 1. Sformułował je fermat w pewnym liście w 1640 roku. Fermat obok Pascala dał początek matematycznej teorii prawdopodobieństwa. Przyczynił się do tego między innymi Chevalier de Mere ,który wiele czasu poświęcił grom hazardowym i notował przebieg i wyniki gier, gdyż pragnął znaleźć najlepszą metodę gry. Zwrócił się on do Pasacala w sprawie "probleme des pointes". Pascal w korespondencji z Fermatem poruszył to zagadnienie, które zapoczątkowało ich wspólną pracę nad teorią prawdopodobieństwa i stworzenia części jego podstaw w 1654roku. Fermat interesował się też zastosowaniem rachunku różniczkowego do zagadnień optyki .Znana jest jego ogólna zasada optyki geometrycznej, która głosi ,że w ośrodku niejednorodnym promień światła
przechodząc od punktu A do punktu B wybiera spośród różnych możliwych dróg, tę, na której przebycie zużywa minimum czasu. Zasada ta ma duże znaczenie w zagadnieniu układów soczewek. Przed z górą półtora tysiącem lat zagadnieniem tym interesował się Heron z Aleksandrii, lecz Fermat uzupełnił je i udowodnił. Ponadto rozważał zagadnienie znalezienia pewnej ogólnej zasady, łączącej prawa Wszechświata. Fermat umarł w Tuluzie, w 1665. Powrót
BLAISE PASCAL(1623-1662) :Znakomity francuski matematyk, fizyk, filozof Błażej Pascal urodził się 19 czerwca 1623 roku w mieście Clermont. Uczony ten już w dzieciństwie zdradzał nieprzeciętne zdolności. Dlatego też ojciec jego, człowiek wykształcony, chcąc ułatwić rozwój umysłowy syna, przeniósł się do Paryża. Do rozbudzenia zainteresowań młodego Pascala przyczyniła się niewątpliwie jego obecność na zebraniach naukowych, które organizował ojciec. Tematem tych zebrań były m.in zagadnienia matematyczne. Chociaż po pewnym czasie, w obawie przed przeciążeniem umysłowym, ojciec odsunął syna od zebrań i pozbawił literatury matematycznej, dwunastoletni Błążej Pascal stał się autorem wielu twierdzeń z geometrii Euklidesa. Odtąd bez przeszkód mógł oddać się rozważaniom geometrycznym. Na rezultaty nie trzeb było długo czekać.
Mając zaledwie 16 lat napisał pracę "O przecięciach stożkowych". Jego imieniem nazwana została pewna krzywa płaska - tak zwany ślimak Pascala. On również skonstruował automatyczne liczydło do wykonywania czterech działań. Zainteresowania matematyczne Pascala nie ograniczały się jedynie do geometrii;pozostawił prace z arytmetyki teoretycznej i algebry, ponadto odkrył sposób obliczania współczynników Newtona. Mianowicie: współczynniki w rozwinięciu n-tej potęgi dwumianu są elementami trójkąta Pascala - tablicy liczb w kształcie trójkąta, z których każda jest sumą dwu liczb znajdujących się bezpośrednio nad nią, po obu jej stronach. Pascal przyczynił się też do stworzenia podstaw rachunku prawdopodobieństwa i częściowo rachunku różniczkowego. Nazwisko Pascala jest cytowane nie tylko w literaturze matematycznej; zawdzięcza mu wiele także fizyka i filozofia. W dziedzinie fizyki sformułował wniosek
z zasady Torricellego, według którego wysokość słupka rtęci utrzymywanego przez ciśnienie powietrza musi być mniejsza na szczytach gór niż u ich podnóży (wniosek ten został sprawdzony doświadczalnie przez jego szwagra).Stwierdzenie to miało ważne znaczenie dla meteorologii. Poza tyn Pascal jest odkrywcą prawa (prawa Pascala), według którego ciśnienie wywarte na ciecz rozchodzi się wewnątrz cieczy równomiernie we wszystkich kierunkach. W filozofii był zwolennikiem jansenizmu - potępionego przez papieży reformatorskiego prądu filozoficznego w katolicyzmie francuskim, skierowanego głównie przeciwko jezuitom. Główne i najbardziej znane jego dzieło filozoficzne "Myśli" jest uważane obok "Wyznań św. Augustyna" za klasyczne dzieło piśmiennictwa religijnego. Pascal był wątłego zdrowia;większą część życia chorował. W 1646 roku, dotknięty paraliżem, stracił władzę w nogach;żył w odosobnieniu.
Prowadził religijny i ascetyczny tryb życia. Jego pogląd na świat jest wynikiem rozumowania, które nazywa się "zakładem Pascala". Pascal twierdził ,że niewiele się ryzykuje postępując w życiu tak, jak-gdyby Bóg istniał;jeśli jest to tylko urojenie, to i tak się wszystko kończy z chwilą śmierci;jeśli byłoby to prawdą, wygrywa się całą stawkę nieśmiertelności. Błażej Pascal zmarł 19 sierpnia 1662 roku w wieku 39 lat. Powrót
ADAM ADAMANDY KOCHAŃSKI(1631-1700) : Druga połowa XVII wieku była okresem zastoju w rozwoju umysłowości polskiej. Z okresu tego pochodzi jednak postać matematyka polskiego Adama Kochańskiego. Kochański urodził się 5 sierpnia 1631 roku w Dobrzyniu nad Wisłą w rodzinie szlacheckiej. Kształcił się na założonym w 1578 roku Uniwersytecie Wileńskim (nazywanym wówczas Akademią Wileńską). Po ukończeniu nauki wykładał na nim matematykę. W 1654 roku opuścił kraj i przebywał kolejno : W Wurzburgu, Moguncji, Florencji i Pradze. W czasie pobytu poza krajem uzupełnił swe wykształcenie;prowadził także liczne wykłady z zakresu matematyki. Około roku 1680 powraca do kraju, ponieważ powołany zostaje na bibliotekarza i matematyka nadwornego króla Jana III Sobieskiego oraz na nauczyciela królewicza Jakuba. Kochański nie cieszył się dobrym zdrowiem. W roku 1695 w celu leczenia
wyjechał do Cieplic (wówczas w Czechach),gdzie umarł prawdopodobnie 19 maja 1700 roku. Kochański poza wspomnianą już pracą dydaktyczną oddawał się studiom naukowym. Częściowo przedmiotem jego rozważań była mechanika, zajmował się zagadnieniem momentów, opracował i wykonał projekt nowego rodzaju chronometru. Przede wszystkim jednak był matematykiem. Pozycję w światowym piśmiennictwie matematycznym, mającym obecnie wartość raczej historyczną, zapewnił sobie przybliżoną rektyfikacją okręgu. Jak wiadomo, zadania polegało na zbudowaniu przy użyciu liniału i cyrkla odcinka, którego długość równa byłaby długości danego okręgu. Przy końcu XIX wieku udowodniono ,ze konstrukcja taka (dokładna) jest niemożliwa. Przybliżonych rozwiązań danego zagadnienia jest jednak kilka. Jednym z nich jest rozwiązanie Kochańskiego. Opublikował je na łamach założonego przez Leibniza czasopisma naukowego - "Acta Eruditorum"
(opublikował w nim także szereg innych swych prac). Rozwiązanie Kochańskiego odznacza się prostotą i bardzo dobrym przybliżeniem: zostało ono powszechnie uznane i do niedawna stanowiło materiał podręcznikowy. Będąc uczonym na miarę europejską, prowadził obszerną korespondencję z wielu uczonymi, na przykład z Leibnizem (korespondencja ta została zamieszczona w XII (1901) i XIII (1902) tomie "Prac Matematycznych"). Dzięki niej Kochański był chyba jedynym Polakiem, któremu w końcu XVII wieku znane były elementy rachunku różniczkowego. Matematyka polska zawdzięcza Kochańskiemu to ,że jako jeden z pierwszych zapewnił jej w świecie zaszczytną opinię. Powrót
GOTTFRIED LEIBNIZ(1646-1716) : Wielki niemiecki uczony, Gottfried Wilhelm Leibniz urodził się w Lipsku 26 czerwca 1646 roku. gdy miał sześć lat, umarł mu ojciec - prawnik i profesor filozofii na uniwersytecie w Lipsku. Środowisko, w jakim urodził się i wychował, wpłynęło na wczesne rozbudzenie zainteresowań naukowych .Studiował na uniwersytetach w Lipsku i Jenie (w tym ostatnim słuchał wykładów z filozofii i matematyki Weigla). W pierwszym okresie jego kariery naukowej w polu zainteresowań znajdowały się przede wszystkim prawo i filozofia. W roku 1666 uzyskał tytuł doktora praw;warto wspomnieć ,że wcześniejsze rozprawy z lat 1664,1665,1666 kwalifikowały go do tego tytułu,którego jednak mu nie nadano z powodu zbyt młodego wieku. Proponowanej mu wówczas katedry nie przyjął ,ponieważ nigdy nie przejawiał zainteresowania do tego rodzaju pracy. Chętnie natomiast dużą część
życia wypełnił działalnością polityczną. Podróżując do wielu stolic europejskich, miał możność zawierania znajomości z wybitnymi osobistościami politycznymi i naukowymi;czynił to chętnie, gdyż wraz z pracą o charakterze dyplomatycznym prowadził rozległe studia. Równolegle ze stwierdzeniem ,spotykanym w podręcznikach filozofii, że Leibniz był przede wszystkim filozofem, można stwierdzić, iż był przede wszystkim matematykiem. Pierwsze jego prace matematyczne pochodzą z lat : 1668 i 1671. Na wykształcenie matematyczne Leibniza wpłynęły poważnie podróże do Paryża i Londynu. Na okres pobytu w Paryżu przypadają owocne dyskusje z Huygensem oraz skonstruowanie maszyny do liczenia, co zwróciło na Leibniza uwagę uczonych. Wspomniany okres to jednak przede wszystkim studiowanie osiągnięć współczesnej mu matematyki;było to konieczne, bo mając lat 27 rozporządzał,jak sam mówił,nikłymi wiadomościami matematycznymi. Nie przeszkodziło to,by
wkrótce stał się współtwórcą rachunku różniczkowego i całkowego. Uzasadnienie znaczenia tego faktu dla rozwoju matematyki i przyrodoznawstwa jest chyba zbyteczne. Stworzenie rachunku różniczkowego i całkowego jest najważniejszą zasługa Leibniza w dziedzinie matematyki oraz największym dziełem jego życia. Jeszcze przed Leibnizem znane były pewne luźne elementy rachunku różniczkowego,jak np. umiejętność wyznaczania ekstremów czy prowadzenia stycznych. Zasługa Leibniza było stworzenie z tego pełnego systemu pojęć i twierdzeń analizy matematycznej. Pierwsza, liczącą sześć stron pracę z rachunku różniczkowego opublikował w roku 1684 w założonym przez siebie czasopiśmie matematycznym "Acta Eruditorum". Podał w niej pojęcie i symbol różniczki oraz przytoczył bez dowodów reguły różniczkowania sumy, iloczynu, ilorazu i funkcji złożonej oraz zasady wyznaczania ekstremów i punktów przegięcia. Z kolei w roku 1686 podał pojęcie i symbol całki,a znany
wzór Leibniza pochodzi z roku 1695. Skuteczność stworzonego przez Leibniza rachunku różniczkowego została sprawdzona przy rozwiązywaniu wielu zagadnień mechaniki (np. zagadnienie brachistochrony). Prace Leibniza zawierały pewne niejasności i niekonsekwencje. Mimo to stanowiły początek niezwykle płodnego okresu twórczości matematycznej. Do rozpowszechnienia nauki Leibniza przyczynili się przede wszystkim bracia Bernoulli i L`Hospital. Jest charakterystyczne, że Leibniz nie pozostawił po sobie dzieła na miarę swych zdolności. wyniki swych dociekań zawarł w drobnych artykułach i licznej korespondencji (między innymi z A.Kochańskim). Drugim ważkim elementem w dorobku naukowym Leibniza jest jego symbolika. To właśnie on jest twórcą współczesnej symboliki rachunku różniczkowego i całkowego. Do wprowadzonych symboli przywiązywał ogromną wagę i z całą świadomością używał takiego a nie innego symbolu. "Należy zatroszczyć się o to - pisał-by znaki matematyczne
były wygodne dla odkryć" Od niego pochodzą symbole różniczek dx,d2x,d3x, całkowania, równości =; do niego należą również terminy:"funkcja", "współrzędne", oraz wyprowadzenie podwójnych wskaźników dla zapisywania współczynników przy niewiadomych w równaniu z układu równań(pisał3C, tzn. C3, 1C tzn.C1, 10+11x+12y=0, tzn, A10+A11x +A12y=0).Trafność w doborze symboli widać szczególnie wyraźnie na przykładzie symbolu do całkowania: , w symbolu tym odzwierciedlona jest nie tylko funkcja podcałkowa i zmienna całkowania. ale też sam proces operacji całkowania. temu wielkiemu człowiekowi los spłatał figla .Choć we wszelkiej działalności odznaczał się dążnością do godzenia przeciwnych poglądów, uwikłał się w ostatnich latach swego życia w spór z Newtonem o pierwszeństwo w stworzeniu rachunku różniczkowego. Spór ten był szczególnie rozdmuchiwany przez zwolenników obu uczonych.
Prawda zaś wyglądała chyba tak: pierwsze rezultaty uzyskał Newton. Leibniz do odkrycia doszedł na innej drodze (przy zagadnieniu poszukiwania stycznej do krzywej) i zupełnie samodzielnie. Poza tym rezultaty Leibniza były wcześniej dostępne ogółowi matematyków, bo wcześniej były publikowane. Rachunek różniczkowy Leibniza odznaczał się trafniejszą symboliką i stanowił samodzielny rozdział matematyki, gdy dla Newtona był jedynie środkiem dla rozwiązywania zagadnień z mechaniki. Należy jednak zaznaczyć ,że Leibniz w latach 1673,1676 był w Londynie i zawarł tam znajomość Newtonem. Wspomniany spór zatruł schyłek życia Leibniza. Umarł 14 listopada 1716 roku w Hanowerze. Za trumną szedł tylko jeden wierny jego przyjaciel. akademia Berlińska i Królewskie Towarzystwo Londyńskie przemilczały tendencyjnie śmieć tego wielkiego uczonego. Powrót
, w symbolu tym odzwierciedlona jest nie tylko funkcja podcałkowa i zmienna całkowania. ale też sam proces operacji całkowania. temu wielkiemu człowiekowi los spłatał figla .Choć we wszelkiej działalności odznaczał się dążnością do godzenia przeciwnych poglądów, uwikłał się w ostatnich latach swego życia w spór z Newtonem o pierwszeństwo w stworzeniu rachunku różniczkowego. Spór ten był szczególnie rozdmuchiwany przez zwolenników obu uczonych.
Prawda zaś wyglądała chyba tak: pierwsze rezultaty uzyskał Newton. Leibniz do odkrycia doszedł na innej drodze (przy zagadnieniu poszukiwania stycznej do krzywej) i zupełnie samodzielnie. Poza tym rezultaty Leibniza były wcześniej dostępne ogółowi matematyków, bo wcześniej były publikowane. Rachunek różniczkowy Leibniza odznaczał się trafniejszą symboliką i stanowił samodzielny rozdział matematyki, gdy dla Newtona był jedynie środkiem dla rozwiązywania zagadnień z mechaniki. Należy jednak zaznaczyć ,że Leibniz w latach 1673,1676 był w Londynie i zawarł tam znajomość Newtonem. Wspomniany spór zatruł schyłek życia Leibniza. Umarł 14 listopada 1716 roku w Hanowerze. Za trumną szedł tylko jeden wierny jego przyjaciel. akademia Berlińska i Królewskie Towarzystwo Londyńskie przemilczały tendencyjnie śmieć tego wielkiego uczonego. Powrót
JACQUES BERNOULLI(1654-1705) : Do historii matematyki wpisało się ośmiu uczonych o nazwisku Bernoulli, ale do najbardziej znanych należy trzech : Jakub, Jan i Daniel. Jakub urodził się w Bazylei;rodzina Bernoullich przywędrowała z Holandii do Szwajcarii w XVI wieku. Znaczny wpływ na rozwój nauki w Bazylei miał wówczas patrycjat kupiecki, do którego zaliczała się również rodzina Bernoullich. Jakub z woli ojca studiował teologię, ale interesowała go również matematyka,której poświęcał wiele czasu. Matematyczne wykształcenie uzupełnił w Holandii, Anglii i Francji. Po powrocie z podróży bez reszty zajął się studiowaniem matematyki i astronomii. Dwie ogłoszone prace z astronomii nie przyniosły mu oczekiwanego rozgłosu. Rok 1687 był szczególnie ważny dla Jakuba, w roku tym bowiem objął katedrę matematyki na uniwersytecie w Bazylei i rozpoczął owocną korespondencję z Leibnizem. Jak wiadomo, pierwsza praca Leibniza z rachunku
różniczkowego ukazała się w roku 1684; Jakub Bernoulli zapoznał się z nią w 1687;wiadomo jest również ,ze była ona dość zawiła i zawierała wiele błędów drukarskich. Dlatego Jakub wystosował list do jej autora z prośbą o wyjaśnienia. Leibniz otrzymał ten list dopiero w 1690 roku. Z tej przyczyny Jakub był zmuszony do prawie samodzielnego opanowania rachunku Leibniza. Tym cenniejsze wydaje się rozwiązanie przez niego w r. 1690 zadania Leibniza z roku 1687 o izochronie(tj. krzywej, po której spadające ciało w różnych odcinkach czasu przebywa równe wysokości)przy pomocy nowego rachunku. Izochroną okazała się parabola pół sześcienna. We wspomnianej pracy Jakub pierwszy użył dla symbolu całki Leibniza terminu "integral". Leibniz szybko poznał rozwiązanie Jakuba Bernoulliego, ponieważ zostało ono opublikowane w "Acta Eruditorium" ,gdzie - jak wiadomo -ogłaszał swoje prace. Nic też dziwnego ,ze w liście będącym odpowiedzią na list Jakuba z roku 1687 zaproponował mu współpracę.
Ważną częścią analizy matematycznej jest rachunek wariacyjny (taką nazwę noszą metody wyznaczania najmniejszych i największych wartości funkcjonałów tj. funkcji, których polem są funkcje albo układy funkcji,a wartościami liczby rzeczywiste). Powszechnie słusznie uznaje się ,że twórcą rachunku wariacyjnego był Euler. Mimo to dużym krokiem naprzód w rozwoju rachunku wariacyjnego (pasjonował on już uczonych w starożytności) był rozwiązanie przez Jakuba postawionego przez jego brata Jana w roku 1696 zadania o brachistochronie .Zadanie to w żądanym terminie rozwiązał także Newton (anonimowo i bez dowodu) oraz L`Hospital. Najbardziej jednak ciekawe i ważne dla rozwoju rachunku wariacyjnego było rozwiązanie Jakuba, a to z tej przyczyny ,że stanowiło pierwszą próbę zastosowania rachunku różniczkowego do rozwiązywania zadań wariacyjnych. Jakub Bernoulli nie tylko rozwiązywał zadania, ale również am je stawiał (np. zadanie o linii łańcuchowej). Interesowały go krzywe specjalne; do ich badania
używał także współrzędnych biegunowych. Najbardziej zajmowała go spirala logarytmiczna;odkrył jej ciekawe własności. Jest ona wyryta na jego grobie (takie było jego życzenia) i zaopatrzona napisem: "Tak samo powstaję choć się zmieniam". jego imię nosi krzywa "lemniskata Bernoulliego", będąca miejscem geometrycznym punktów (x,y) dla których iloczyn odległości od dwóch punktów stałych F1(c,0) i F2(-c,0) jest wielkością stałą c2. Uczony także duże zasługi położył w teorii szeregów. Jego publikacje z okresu 1689-1704 stanowiły pierwszy przewodnik z tej dziedzinie matematyki. Druga dziedziną,obok rachunku różniczkowego, w której zapisał się trawle jest rachunek prawdopodobieństwa. Dla potrzeb rachunku prawdopodobieństwa rozwinął analizę kombinatoryczną; zupełnie świadomie pierwszy na równi z prawdopodobieństwem a priori wprowadził prawdopodobieństwo a posteriori. Podstawowym dorobkiem w tej dziedzinie był dowód twierdzenia, które obecne jest znane jako
twierdzenie Bernoulliego. Rachunek różniczkowy jest trudnym i subtelnym działem matematyki wyższej. W ujęciu Leibniza, z jakim spotkał się Jakub Bernoulli był zagmatwany. Był również nowym działem matematyki. Należało go więc rozwinąć i zdobyć dla niego zwolenników, którzy by go dalej rozwijali. Można to było uczynić przez wykorzystanie go jako narzędzia do rozwiązywania pewnych zagadnień z mechaniki, jak również samej matematyki. Wśród matematyków, którzy pierwsi wykonali to zadanie, wymienić należy Jakuba Bernoulliego. Powrót
IZAAK NEWTON(1642-1727) : Każdy z nas zna historyjkę o tym ,jak to Newton obserwował w ogrodzie spadające z drzew jabłka. To stało się dlań podobno bodźcem do odkrycia jednego z najbardziej podstawowych praw rządzących przyrodą-prawa powszechnego ciążenia. Jest to oczywiście tylko anegdota,gdyż stworzenie teorii grawitacji nie było dziełem przypadku,lecz dziełem genialnego umysłu tego wielkiego fizyka i matematyka. Newton urodził się w rodzinie ubogiego farmera w Woolsthorpe,niedaleko Cambridge w Anglii. Po skończeniu szkoły wstąpił do Trinity College(jednego z "colleg`ów" Cambridge),po skończeniu którego otrzymał stopień magistra (1668). Jego nauczyciel przekazuje mu katedrę matematyki i fizyki na uniwersytecie w Cambridge, którą Newton piastuje aż trzydzieści dwa lata. Pierwsze wykłady ma z dziedziny optyki. Według słów samego Newtona najbardziej owocne lata jego pracy naukowej przypadają na okres 1665-1666.Nie ma innych przykładów osiągnięć w historii nauki
godnych porównania z osiągnięciami Newtona w okresie tych dwóch złotych lat. Wtedy to tworzy jako pierwszy (równolegle z Leibnizem)podstawy rachunku różniczkowego i całkowego,zaczyna pracować nad swoim wielkim dziełem o optyce "New Theory about Light and Colours"("Nowa teoria światła i kolorów") oraz tworzy podstawy teorii powszechnego ciążenia. On pierwszy wskazuje na fakt ,że promień światła białego rozszczepia się po przejściu przez pryzmat na promienie o różnych kolorach. Jego praca o optyce wywołała gorące dyskusje w świecie naukowym na temat natury światła. Te genialne idee narodziły się w umyśle Newtona podczas pobytu w rodzinnej wsi, gdzie schronił się przed epidemią panującą w Cambridge. Największym jednak dziełem Newtona było "Philosophiae naturalis principia mathematica" ("Matematyczne podstawy filozofii naturalnej") wydane w 1687 roku, W dziele tym sformułował trzy podstawowe zasady mechaniki klasycznej oraz prawo grawitacji, na podstawie którego opracował teorię ruchów planet i wyjaśnił wiele
innych problemów w astronomii (m.in powstawanie przypływów i odpływów mórz na Ziemi na skutek przyciągania Księżyca). W 1672 Newton zostaje wybrany członkiem londyńskiego Royal Society, później zaś jego przewodniczącym. Poważna choroba, na którą zapadł w 90 latach XVII wieku, wywołała w całym świecie naukowym duże zaniepokojenie. Świadczą o tym chociażby listy,jakie wymieniają między sobą tacy wybitni matematycy jak Huygens i Leibniz. Choroba mija jednak i w tym samym roku Newton zostaje członkiem Paryskiej Akademii Nauk. Rok później Jan Bernoulli rozesłał do wszystkich najwybitniejszych współczesnych matematyków dwa problemy do rozwiązania, dając im sześć miesięcy na rozwiązanie. Po krótkim dosyć czasie otrzymuje ku swemu zdziwieniu anonimowo nadesłane rozwiązanie. Domyślił się jednak ,że autorem tego mógł być tylko Newton. Niestety dość trudno ocenić wpływ osiągnięć naukowych Newtona na współczesnych , gdyż prace swe ogłaszał ze znacznym opóźnieniem. Na przykład prawo grawitacji, które odkrył w latach 1665-66
ogłosił w dwadzieścia lat później. Dzieło "Arithemtica uniwersalis" ,zawierające wykłady algebry wygłaszane w latach 1673-1683, opublikował dopiero w 1707 roku. Również podstawy rachunku różniczkowego ukazały się po opublikowaniu pracy Leibniza, mimo ,że Newton pracę tę napisał około dziesięciu lat przed Leibnizem. W 1727 r. wskutek przewlekłej choroby umiera. Jak wielka była jego pasja tworzenia,chęć nieprzerwanej walki na polu nauki, mogą świadczy jego trochę może żartobliwe słowa : "Nauka jest jak kłótliwa i piękna kobieta. Jeśli chcesz mieć z nią do czynienia, musisz prowadzić wiecznie proces sądowy". Powrót
JEAN BERNOULLI(1667-1748) : Drugim wybitnym uczonym i aktywnym współpracownikiem Leibniza był obok Jakuba Bernoulliego, jego brat Jan. Żył w latach 1667-1748. Miał zostać kupcem ,ale zamiłowania jego szły w innym kierunku, ku matematyce, której nauczył się od starszego o trzynaście lat brata Jakuba. W latach 1691/92 przebywał w Paryżu, gdzie w okresie tym idee Leibniza były prawie zupełnie nieznane. Poznał tu matematyka francuskiego markiza L`Hospitala, dla którego spisał wiadomości z rachunku całkowego. Stanowią one pierwszy systematyczny wykład tego rachunku (drukiem zostały wydane dopiero w roku 1742) W wykładzie tym całkę rozumie prawie w sensie współczesnym;zawierała ona stałą dowolną;operacja całkowania była dla Jana Bernoulliego operacją odwrotną do różniczkowania. W roku 1692 Bernoulli wrócił do Bazylei. W dwa lata później uzyskał tu stopień doktora medycyny, w której dla objaśnienia ruchu mechanicznego mięśni zastosował rachunek różniczkowy .W roku
1693 nawiązał korespondencję z Leibnizem, która podobnie jak w przypadku brata przyczyniła się do rozwoju matematyki. OD roku 1695 był profesorem matematyki na uniwersytecie w Groningen w Holandii, a w roku 1705 objął katedrę matematyki na uniwersytecie w Bazylei, po śmierci brata Jakuba. Zasługi Jana Bernoulliego dla rozwoju rachunku różniczkowego i całkowego są liczne i powiązane z osiągnięciami Jakuba Bernoulliego i Leibniza. Do poważniejszych należą wspomniane już prace z rachunku całkowego. Wspólnie z Leibnizem wskazał metodę całkowania funkcji wymiernej (przez rozkład na ułamki proste), przy czym nie odstraszała go nawet zmienna zespolona. Do Jana Bernoulliego należy zdefiniowanie w roku 1718 terminu funkcji,aczkolwiek używał go już znacznie wcześniej. Każdemu kto zetknął się z analizą matematyczną, znane jest tzw. twierdzenia L`Hospitala, podające sposób wyznaczania granicy w pewnym punkcji ilorazu f(x) : f(x)/g(x) , funkcji różniczkowych, gdy granica w tym punkcie licznika i mianownika jest równa zeru.
Metodę wyznaczania granic takich ilorazów podał Jan Bernoulli, co dowodzi, że twierdzenie to niesłusznie nosi imię L`Hospitala. W 1706 , Jan Bernoulli postawił następujące zadanie: spośród wszystkich krzywych płaszczyzny pionowej łączących punkty A i B nie leżące na prostej pionowej znaleźć tę ,dla której punkt materialny ślizgający się po niej pod wpływme siły ciężkości i mający w punkcie A prędkość początkową równą zeru dojdzie w najkrótszym czasie do punktu B. Ta krzywa najszybszego spadku była już poszukiwana przez Galileusza, z tym ,że nazwę "brachistochrona" otrzymała od Jana Bernoulliego. Brachistochroną jest łuk cykloidy. Postawienie tego zadania wtedy gdy zbudowane były pewne elementy rachunku różniczkowego, stanowiło ważny moment w rozwoju rachunku wariacyjnego. Pierwsze rozwiązanie Jana Bernoulliego oparte było na pewnej analogii wziętej z optyki. W rozwiązaniu Jakuba Bernoulliego własność (dotycząca dowolnie małego łuku brachistochrony),którą Jan wziął z optyki, została udowodniona. Tę
niedoskonałość zarzucał Jakub bratu. Od tego czasu na dobre rozgorzał spór między uczonymi braćmi, który zakończył się dopiero w chwili śmierci Jakuba (spór ten dotyczył i innych zagadnień, np. izoperymetrów). Badaniom ich towarzyszyła ciągła rywalizacja, która z kolei zwiększała intensywność tych badań. To stanowiło korzystną stronę sporu. Obydwaj stawiali i rozwiązywali zadania. do ważnych z punktu widzenia rozwoju analizy matematycznej należy rozwiązanie przez Jana Bernoulliego zadania brata o linii łańcuchowej. Rozwiązanie to podali także Leibniz i Huygens. Jan Bernoulli i Leibniz rozwiązali je przy użyciu rachunku różniczkowego, natomiast nie umiejący się posługiwać tym rachunkiem Huygens rozwiązał je przy użyciu starych metod. Wynik otrzymali jednak ten sam. Stanowiło to wspaniały sprawdzian poprawności i użyteczności nowych metod. Pionierskie są zasługi Jana Bernoulliego w dziedzinie równań różniczkowych. Jedno z ważnych typów takich równań znane jest jako równanie Bernoulliego. Przy całkowaniu równań
różniczkowych Bernoulli stosował także metodę czynnika całkującego oraz rozwijanie na szeregi potęgowe. Do jego uczniów poza L`Hospitalem, należy syn Daniel i genialny Euler. Godne podkreślenia jest to ,że osiągnięcia i badania Jana Bernoulliego łączyły się ściśle z zastosowaniami, zgodnie z resztą z postulowaną przez niego tezą iż uczony zawsze powinien znajdować się w "granicach przyrody". Powrót
ABRAHAM DE MOIVRE(1667-1754): Abraham de Moivre urodził się w 1667roku w Vitry we Francji. Pochodził z drobnej szlachty francuskiej; był protestantem. Od 1681 roku studiował filozofię. Po odwołaniu edyktu nantejskiego (1685 r.) by uniknąć prześladowań, wyjechał do Anglii i tu pracował jako prywatny nauczyciel. Pozostawał z bliskich stosunkach z Newtonem. W Anglii przebywał do końca życia, wydawał prace matematyczne w języku angielskim i uchodził za angielskiego matematyka pochodzenia francuskiego. Korzystał z "Algebry" Wallisa (1685) i "Zasad" Newtona (1687). Przez pewien czas zajmował się fluksjami Newtona. Zbadał szeregi potęgowe i pierwszy korzystał z potęgowania szeregów nieskończonych. Zajmował się kombinatoryką i zagadnieniami rachunku prawdopodobieństwa, w których występuje liczba n! (silnia oznacza iloczyn kolejnych liczb naturalnych od 1 do n). Liczba n! ze zwiększeniem n szybko rośnie. Już 10! = 3 628 800. Rachunki stają się żmudne. Moivre wykazał
dogodny sposób obliczania przybliżonej wartości n!. Dziś korzysta się ze wzoru Stirlinga. W 1733 roku ogłosił pracę, w której udowodnił ,że dla dużej liczby n doświadczeń funkcja rozkładu normalnego prawdopodobieństwa jest przybliżeniem prawa dwumianowego. Do podstawowych twierdzeń prawdopodobieństwa zalicza się twierdzenie Movire`a - Laplace`a. W podręcznikach szkolnych algebry, podany jest słynny wzór de Movire`a i jego zastosowanie:
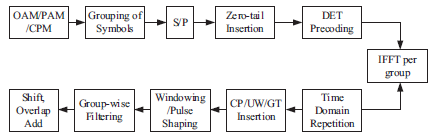
gdzie 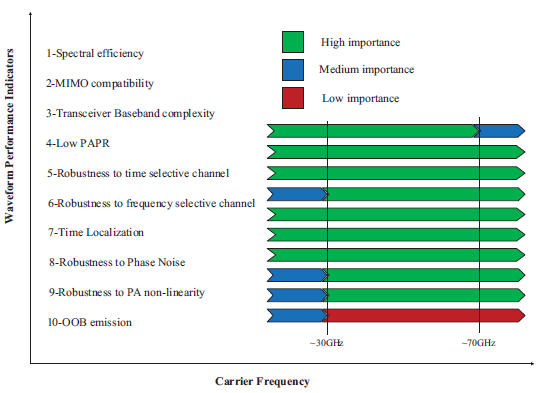 jest jednostką urojoną. Wzór de Movire`a pozwala obliczyć wszystkie wartości n pierwiastków n-tego stopnia z liczby a. Na przykład z liczby 1 istnieją cztery pierwiastki czwartego stopnia, są nimi :1,-1, i, -i. Wiąże się to z zagadnieniem podziału okręgu na n równych części i wy,aga rozwiązania równania cyklotomicznego (równania podziału okręgu). Współczesny zapis wzoru de Movire`a zawdzięczamy Eulerowi .Movire był członkiem Londyńskiego Królewskiego Towarzystwa Naukowego od 1697 roku a także członkiem Paryskiej i Berlińskiej Akademii Nauk. Umarł w Londynie w 1754 roku. Powrót
jest jednostką urojoną. Wzór de Movire`a pozwala obliczyć wszystkie wartości n pierwiastków n-tego stopnia z liczby a. Na przykład z liczby 1 istnieją cztery pierwiastki czwartego stopnia, są nimi :1,-1, i, -i. Wiąże się to z zagadnieniem podziału okręgu na n równych części i wy,aga rozwiązania równania cyklotomicznego (równania podziału okręgu). Współczesny zapis wzoru de Movire`a zawdzięczamy Eulerowi .Movire był członkiem Londyńskiego Królewskiego Towarzystwa Naukowego od 1697 roku a także członkiem Paryskiej i Berlińskiej Akademii Nauk. Umarł w Londynie w 1754 roku. Powrót
LEONARD EULER(1707-1783) : Euler należy niewątpliwie do najbardziej genialnych i płodnych matematyków wszystkich czasów. Jego imię stawia się w historii nauk ścisłych na równi z Newtonem, Descartem, Galileuszm. Był nie tylko matematykiem ,ale także fizykiem i astronomem. Prace jego wywarły olbrzymi wpływ na rozwój tych nauk. Urodził się w Szwajcarii. W Bazylei słuchał wykładów wielkiego matematyka Jana Bernoulliego, który zaofiarował się osobiście kierować rozwojem talentu młodego Eulera. Mając 16 lat otrzymał już Euler stopień magistra. W cztery lata później wyjechał do Rosji na zaproszenie Petersburskiej Akademii Nauk, aby stać się jej członkiem i objąć katedrę fizjologii. Od tego czasu zaczyna się rozwój jego naukowej działalności. Pierwsze jego prace dotyczą nawigacji, lecz później oddaje się naukom matematycznym. Czasopismo Akademii "Komentarze" bez przerwy drukuje jego prace matematyczne. Euler jest znany ze swej niepospolitej pracowitości, wskutek czego
traci jedno oko. Nie przeszkadza mu to jednak w dalszej twóczości. Pracuje nad mapą Rosji, pisze teorię muzyki, a w późniejszych latach wydaje duże dzieło o nawigacji, za które otrzymuje 6000 funtów nagrody od rządu francuskiego. Światowy rozgłos przynosi Eulerowi jego dzieło o mechanice (1736). Niedługo potem otrzymuje wraz z Danielem Bernoullim i Maclaurinem nagrodę od Paryskiej Akademii Nauk za pracę na temat przypływów i odpływów morza. Wskutek wytężonej pracy naukowej stan jego zdrowia pogarsza się niestety i wymaga zmiany warunków. Euler wyjeżdża więc do Berlina. Rok po roku ukazują się nowe dzieła Eulera o ruchach planet i komet, o teorii magnetyzmu i na tematy balistyczne. W 1748 wychodzi w Lozannie jego główne trzytomowe dzieło "Wstęp do analizy nieskończenie małych", które jest zbiorem jego dawniejszych prac i artykułów matematycznych pisanych w ciągu wielu lat. Dzieło to ugruntowało jego pozycję jako najwybitniejszego ówczesnego matematyka. Prawie wszystko, co wykłada się obecnie w zakresie
algebry wyższej i analizy matematycznej , jest tu zawarte. Euler między innymi jest autorem znanego twierdzenia, że liczba krawędzi wielościanu jest o dwa mniejsza od sumy liczby wierzchołków i liczby ścian tego wielościanu. Słynne zadanie o mostach w Królewcu ułożył również Euler. Postawił mianowicie pytanie, czy można po siedmiu mostach łączących dzielnicę miasta z wyspą na rzece Pregole odbyć spacer w ten sposób, aby przejść kolejno przez wszystkie osty, nie przechodząc po żądnym z nich więcej niż raz. Próby , które radzimy przeprowadzić ,wykażą ,że jest to niemożliwe. W 1766 Euler wraca do Rosji. Katarzyna II wyznacza mu stałą pensję z własnych funduszów. "Mam nadzieję - mówi -,że moja Akademia odrodzi się z popiołów,gdy do niej powrócił wielki człowiek ".Niestety zaraz po przyjeździe Euler zachorował i stracił drugie oko. Lecz jego geniusz matematyczny i świetna pamięć zastępują mu wzrok Pisał wzory kredą na tablicy oraz dyktował przyjaciołom nowe prace. W ten sposób pojawiła się jego algebra, następnie
owoc jego 30 letniej pracy, dzieło na temat dioptryki oraz wiele innych. Charakterystyczny jest fakt ,że geniusz i płodność twórcza Eulera rozwijały się aż do jego późnej starości, o czym świadczyć może wzrastająca liczba wydawanych przez niego prac. Jeszcze w dzień śmierci toczył,ze swoimi współpracownikami ożywioną dyskusję naukową. Pochowany został na cmentarzu Smoleńskim w Petersburgu. Jeden z jego współpracowników mówił: "W oczach Eulera wzory matematyczne żyły swym własnym życiem i opowiadały istotne i ważne rzeczy o przyrodzie. Wystarczyło mu tylko dotknąć się ich,aby z niemych przeradzały się w mówiące, dające odpowiedzi pełne głębokiego znaczenia." Wielki matematyk francuski Laplace wyraził się o wartości prac Eulera: "Czytajcie Eulera, on jest naszym wielkim nauczycielem". Powrót
JEAN LE ROND d`ALAMBERT(1717-1783) :D`Alebert Jean le Rond, jedne z najbardziej wszechstronnych i wpływowych umysłów osiemnastego wielu, urodził się w Paryżu w 1717 roku jako naturalny syn poety Destontesa i pani de Tencin. Po urodzeniu został podrzucony przez rodziców w kościele St. Jean le Rond. Słabe dziecko wzbudziło litość policji, która oddała je na wychowanie żonie biednego rzemieślnika. Pod jej macierzyńską opieką wyrósł na zdrowego i silnego chłopca. W dwunastym roku życia został oddany do College Mazarin, gdzie zbierał nagrody za doskonałe wyniki w nauce i rozwijał nieprzeciętne zdolności. Interesowało go wiele dziedzin wiedzy, ale najbardziej pociągała go matematyka. Pierwszymi pracami D`Alamberta z dziedziny matematyki i fizyki były rozprawy o ruchu ciał stałych w płynach i o rachunku całkowym, które Akademia Nauk tak wysoko oceniła, że w roku 1741 powołała go na członka. Następna z jego świetnych prac to "Traite de dynamique" (Paryż 1743) i "Traite
de fluides" (1744) oraz "Reflexions sur la cause des vents" (Paryż 1747, za którą otrzymał nagrodę Akademii Nauk w Berlinie i mianowany jej członkiem. Trudno wyliczyć wszystkie prace D`Alamberta,należałoby zwrócić jeszcze uwagę na "traktat o czystej analizie" (1746 i 1748), "O drganiu strun" (1748) oraz pracę z dziedziny astronomii o zboczeniach w biegu eliptycznym planet wokół Słońca i "O posuwaniu się równi dnia z nocą". Bardzo duży wkład wniósł D`Alambert w opracowanie "Encyklopedii" Diderota, do której napisał część matematyczno - fizyczną. We "wstępie do Encyklopedii" podjął i rozwinął koncepcję klasyfikacji nauk Bacona, przyjmując ,że zasadą podziału są władze umysłu ludzkiego. O wszechstronności jego umysłu niech świadczą również prace z dziedziny muzyki i estetyki ("De la liberte en musique" 1759 r.) W mechanice klasycznej jest tzw. zasada D`Alamberta sprowadzająca zagadnienia ruchu bryły sztywnej do zagadnień statyki. Ceniąc własną niezależność, D`Alambert odrzucił zaszczyty i nagrody, jakimi
obdarzali go Fryderyk Wielki i cesarzowa Katarzyna. Powrót
JOSEPH LOUIS LAGRANGE(1736-1813) : Joseph Lagrnage pochodził z Turynu, gdzie urodził sięw 1736 roku w rodzinie urzędnika bankowego. Jako najmłodsze dziecko licznej rodziny,musiał uczynić wszystko,by jak najszybciej zająć samodzielne stanowisko. Początkowo interesował się filologią, lecz pewnego dnia wpadła mu w ręce rozprawa z optyki matematycznej i wtedy poznał swoje właściwe powołanie. Wszystkie siły poświęcił studiom matematycznym i osiągnął to ,że w wieku 17 lat został wykładowcą matematyki w Królewskiej Szkole Artyleryjskiej w Turynie. Chociaż Lagrange był młodszy od swoich uczniów, cieszył się opinią świetnego nauczyciela. W roku 1757 założył wspólnie ze swoimi byłymi uczniami Akademię Turyńską, mającą początkowo charakter prywatnego stowarzyszenia naukowego. Lagrange był przewodniczącym sekcji matematyczno-fizycznej. W 1759 roku ukazał się I tom sprawozdań Akademii "Actes de la Societe prive" .W tomie tym znajduje się wiele prac 23 letniego uczonego,
przeważnie z rachunku wariacyjnego i jego powiązania z mechaniką. Opierając się na pracach Eulera, Lagrange opracował podstawowe pojęcia rachunku wariacyjnego oraz podał metodę rozwiązania problemów wariacyjnych. Euler po zapoznaniu się z tymi pracami tak, napisał w liście do Lagrange`a : "...Pańskie rozwiązanie problemów izoperymetrycznych jest bez zarzutu i cieszę się ,że ten temat, którym od dawna się zajmowałem, został przez Pana doprowadzony tak blisko do ostatecznego zakończenia .." .W tym samym roku Lagrange zostaje członkiem Berlińskiej Akademii Nauk. Na skutek nadmiaru pracy Lgrange już w wieku 25lat ciężko zapadł na zdrowiu. Niestety jedynym środkiem, jaki znała ówczesna medycyna, było puszczanie krwi. Zabieg ten przeprowadzano mu aż 29 razy. Nic więc diznwego,że opadał z sił coraz bardziej. W 1766 roku uczony przeniósł się do Berlina, gdzie otrzymał stanowisko przewodniczącego Berlińskiej Akademii Nauk, które piastował przez 20 lat. W tym czasie pracował niezwykle wydajnie. Przeciętnie co miesiąc
ogłaszał nową rozprawę. Z jego berlińskich prac najważniejsza jest teoria równań różniczkowych cząstkowych. W roku 1772 Lagrange zostaje członkiem Akademii Paryskiej. Uczony jednak nie mógł dostosować się do ostrego klimatu berlińskiego i w 1787 roku wrócił do Paryża gdzie wykładał na wyższych uczelniach. W 1788 roku w swoim klasycznym traktacie "Mechanika analityczna" rozszerzył podstawy statystyki i mechaniki, podając "ogólną formułę" znaną dzisiaj jako zasada najmniejszego działania. Lagrange w ciągu całego swojego życia ogłosił wiele prac z zakresu analizy matematycznej (reszta Lagrange`a we wzorze Taylora) teorii liczb, algebry, interpolacji (wzór interpolacyjny Lagrange`a),kartografii matematycznej i astronomii. Prócz prac teoretycznych podkreślić należy udział Lagrange`a w komisji opracowującej wybór nowej jednostki długości (metr) i oparty na niej układ metryczny. Lagrange umarł w 1813 roku w wyniku całkowitego wyczerpania po długotrwałej chorobie. Nad jego trumną wybitny uczony Lapalace tak
scharakteryzował zmarłego: "...wśród tych którzy najefektywniej rozszerzyli granice naszej wiedzy, Newton i Lagrange posiedli w najwyższym stopniu tę szczęśliwą sztukę odkrywania nowych zasad, które stanowią właściwą istotę wiedzy...". Powrót
GASPARD MONGE(1746-1818) :Wśród całej plejady znakomitych matematyków, których ojczyzną jest Francja, Gaspard Monge uchodzi za jednego z najdoskonalszych, a w dziedzinie geometrii za jedną z najwybitniejszych postaci wszystkich czasów. Twórczość Monge`a zbiegła się z bujnym rozwojem szkolnictwa wyższego we Francji, a założenie szkół wojskowych i akademii w ostatnich dziesięcioleciach wieku osiemnastego można uważać za początek nowego okresu matematyki francuskiej. Swą karierę rozpoczął Monge jako instruktor akademii wojskowej w Mezieres. Urodził się w 1746 roku w Beaune,małym miasteczku w Burgundii. Ojciec jego, kupiec i szlifierz, szczerze troszczył się o wykształcenie trzech synów,z których Gaspard był najstarszy i najzdolniejszy .Przez swe szkolne lata przechodził jako prymus. W wieku 14 lat konstruuje sikawkę strażacką, a później sporządza szczegółowy plan swojego miasta, zdradzając duże talenty konstruktora. To żywe zainteresowanie się zagadnieniami
praktycznymi występuje szczególnie wyraźnie podczas studiów Gasparda w akademii wojskowej w Mezieres, w której uchodził za najzdolniejszego. To tutaj właśnie stworzył podstawy nowej metody geometrycznej zwanej geometrią wykreślną. Historia mówi, że jej pomysły nasunęły mu się przy opracowywaniu planów umocnień fortyfikacyjnych na podstawie danych. Jakież było zdziwienie profesora nadzorującego pracę ,gdy Gaspard po krótkim stosunkowo czasie oznajmił mu jej zakończenie. Okazało się ,że zamiast żmudnych, czasochłonnych obliczeń młody Monge zastosował metody wykreślne,znakomicie ułatwiające pracę. Rozwinął je zresztą wkrótce tak dalece ,że stanowiły one potem samodzielny dział geometrii. Niebawem po powstaniu geometrii wykreślnej uczyniono z niej tajemnicę wojskową. W 1768 roku Monge zostaje profesorem matematyki, a w 1771 profesorem fizyki w Mezieres,. Prócz wspomnianych odkryć,ogłoszonych drukiem w "Geometrie descriptive" (1795-1799), Monge zaczął stosować także rachunek różniczkowy i całkowy
do badania krzywych i powierzchni. Jego prace na ten temat zostały później (w 1809 roku) ogłoszone w "Application de l`analyse a la gepometrie" - pierwszym podręczniku geometrii różniczkowej. Z nią związane są też główne odkrycia Monge`a. W roku 1780 zostaje członkiem Akademii Francuskiej, a w 1783 przenosi się do Paryża. Będąc z przekonań politycznych republikaninem, w przeciwieństwie do Laplace`a, potrafił zostać lojalnym w stosunku do Napoleona i chociaż miał dużo trudności w pogodzeniu się z cesarstwem, oddał mu całą duszę widząc w nim wykonawcę ideii rewolucji. Na wieść o katastrofalnej wyprawie Napoleona na Rosję Monge dostaje apopleksji, podczas zaś "stu dni" staje się znowu jego gorącym zwolennikiem. Po klęsce Napoleona nowy rząd mocą dekretu wyklucza w 1816 Monge`a z Akademii. Przez ostatnie lata swego życia Monge był dyrektorem l`Ecole POytechnique, której był czynnym organizatorem. Geometria wykreślna której twórcą był Monge, stanowi obecnie jeden z podstawowych przedmiotów na uczelniach
technicznych. Powrót
PIERRE SIMONE DE LAPLACE(1749-1827) : Urodził sie23 marca 1749 roku w Beaumont w Normandii. Kształcił się w Beaumont i Caen w szkole prowadzonej przez zakon benedyktynów. W 1766 roku przybył do Paryża, gdzie dzięki pomocy d`Alemberta zdobył stanowisko profesora w Paryskiej Szkole Wojskowej. W latach 1779-1784 Laplace wspólnie z Lavoisierem zajmował się zagadnieniami fizycznymi,między innymi ciepłem topnienia ciał. Wielka rewolucja francuska oderwała Laplace`a od jego prac. Powierzona mu została reorganizacja całego systemu szkolnictwa wyższego we Francji. Zajął się tworzeniem szkół wyższych - Szkoły Normalnej i Szkoły Politechnicznej. W 1790 obrano Laplace`a prezesem Urzędu Miar i Wag i z tej racji przyczynił się do wprowadzenia w życie systemu metrycznego. W 1795 powołano go na członka biura zajmującego się pomiarami południka ziemskiego. W latach 1799-1825 opracował ,a następnie wydał pięciotomowe dzieło "Mechanika nieba" i "Analityczną teorię
prawdopodobieństw" (rok 1812). Oba te wielkie dzieła zawierają nie tylko jego własne osiągnięcia, a cały wcześniejszy dorobek w tych dziedzinach. Laplace poza astronomią zajmował się pewnymi zagadnieniami matematyki i fizyki matematycznej. Dość wymienić jego twierdzenie o całkowaniu równań o pochodnych cząstkowych,twierdzenie o przedstawieniu wyznacznika w postaci sumy iloczynów kolejnych elementów dowolnego wiersza albo kolumny przez odpowiadające im tzw. podwyznaczniki (minory), oraz przekształcenie całkowe nazwane jego imieniem. Mimo,że przed Laplacem rachunkiem prawdopodobieństwa zajmowali się między innymi Fermat i Bernoulli,do niego w dużej mierze należy stworzenie matematycznej teorii i udoskonalenie metod dowodów. Rozwinął teorię błędów i metodę najmniejszych kwadratów, udowodnił twierdzenie noszące jego nazwisko, a mające do dziś bardzo poważne znaczenie w rachunku prawdopodobieństwa,jako twierdzenie graniczne. Jego "Analityczna teoria prawdopodobieństwa" była trzykrotnie wydawana za życia uczonego.
Przez całe życie Laplace dzielił swe zainteresowania pomiędzy astronomię, matematykę i fizykę. W 1806 opublikował pracę dotyczącą teorii włoskowatości, w 1809 podał wzór na obliczenie szybkości rozchodzenia się dźwięku w powietrzu, ustalił wzór pozwalający obliczyć ciśnienie atmosferyczne w zależności od wysokości nad ziemią. Zbudował także własną teorię światła. Jego działalność w dziedzinie fizyki spowodowała znaczny rozwój fizyki doświadczalnej. W trakcie badań astronomicznych wykazał ,że prawo powszechnego ciążenia w pełni wyjaśnia ruch planet. W 1780 roku przedstawił pracę dotyczącą metody obliczania orbit ciał niebieskich, a w następnych latach postawił hipotezę ,że pierścień Sturna nie jest jednolity,sam zaś Sturn spłaszczony u biegunów. W 1789 sformułował teorię ruchu satelitów Jowisza i otrzymał całkowitą zgodność z obserwacjami. W 1787 odkrył przyczyny zmian w prędkości ruchu Księżyca, określił wielkość spłaszczenia Ziemi, a w 1788 ogłosił pracę o dynamicznej teorii przypływów. Cały swój dorobek
naukowy w tej dziedzinie zamknął w "Mechanice nieba". Warto zauważyć ,że kosmogoniczna hipoteza Laplace`a tzw hipoteza Kanta i Lapalce`a miała ogromne znaczenie filozoficzne. Ogłosił ją w pracy "Przedstawianie systemu świata" (rok 1796) .W swych poglądach filozoficznych skłaniał się ku materialistom. Mimo iż wychował się w szkole zakonnej, całe życie był ateistą. Jego zaś przekonania polityczne zmieniały się tak,jak zmieniały się rządy we Francji .W okresie rewolucji był obdarzony licznymi zaszczytami. W czasie konsulatu piastował urząd ministra spraw wewnętrznych, a następnie został senatorem. Napoleon w 1811 nadał mu tytuł hrabiego de Laplace,w zamian za co uczony dedykował cesarzowi trzeci tom swej "Mechaniki". Laplace`owi przypisywana jest odpowiedź ,jaką miał dać Napoleonowi na pytanie czemu Bóg nie został wspomniany w jego dziele: "Sir, nie potrzebowałem uciekać się do tej hipotezy". Otrzymane zaszczyty nie przeszkodziły mu jednak w oddaniu w 1814 roku głosu za obaleniem Napoleona. Znamienny jest
również fakt, że po 1814 roku trzeci tom "Mechaniki" dedykował Ludwikowi VIII. W czasie restauracji Burbonów Laplace otrzymuje parostwo i tytuł markiza. Powrót
ADRIAN MARIE LEGENDRE(1752-1833) : Adrian Maria Legendre urodził się 18 września 1752 roku w Paryżu. Dzieciństwo i młodość spędził w rodzinnym mieście, tutaj też kończył COllege Mazarin. Bardzo wcześnie interesował się wszelkiego rodzaju zagadnieniami matematycznymi. Sprzyjają temu rozwijające się we Francji szkoły wojskowe i inżynieryjne, w których szczególny nacisk kładziono na nauki matematyczne. W latach 1775-1780 Legendre pracował jako nauczyciel w szkole wojskowej w Paryżu, następnie prowadził wykłady w l`Ecole Normale. Opracował wtedy kilka zagadnień związanych z balistyką. W 1782 roku otrzymał za te prace nagrodę Akademii Berlińskiej,a w rok później powołano go na członka Paryskiej Akademii Nauk. W latach 1787-1789 Legendre interesował się pracami Monage`a związanymi z równaniami różniczkowymi. Niektóre zagadnienia uogólnił i poszerzył. Zajął się również teorią liczb. W swej książce "Teoria liczb" zgromadził tyle materiału dotyczącego różnych
twierdzeń o liczbach całkowitych, że praca ta zachowała swoją wartość do chwili obecnej. W 1794 roku Legendre wydał podręcznik "Geometrii elementarnej", w której podobnie jak wielu współczesnych mu matematyków starał się udowodnić aksjomat Euklidesa o prostych równoległych. W 1798 r. ukazały się pierwsze prace naukowe Legendre`a tłumaczone na język polski przez Karczewskiego i przez Hreczynę w 1834 roku. W 1799 r. w drugim wydaniu "Geometrii elementarnej" podał dowód ,że suma kątów trójkąta nie może być mniejsza niż 180o. Legender zajmował się między innymi funkcjami eliptycznymi, wyznaczaniem orbit komet, zagadnieniem liczb pierwszych. Doszedł nawet na drodze empirycznej do pewnego wzoru pozwalającego obliczyć z dość dużym przybliżeniem ilość liczb pierwszych w zakresie do jednego miliona. Dowodu jednak nigdy nie podał. Legendre pracował nad wieloma zagadnieniami, którymi zajmował się młodszy od niego o 25 lat Gauss. W 1806 r. odkrył równocześnie z nim metodę najmniejszych kwadratów. Rozwiązywał
niektóre problemy praktyczne, na przykład zajmował się wyznaczeniem stopnia szerokości między Dunkierką i Boulogne. W 1808 r. Legendre mianowany został dożywotnim zwierzchnikiem uniwersytetu, w 1816 egzaminatorem w l`Ecole Politechnique, a wkrótce potem inspektorem geodezyjnym. W latach 1816 i 1825 Legendre podał uzupełnienie do drugiego wydania "Teorii liczb". Powrót
JAN ŚNIADECKI(1756-1830) : Po wspaniałym rozkwicie Uniwersytetu Krakowskiego, około połowy XVi w., następuje jego upadek i zastój. Drugą postacią ,obok Kołłątaja, która przyczyniła się w sposób istotny do ponownego ożywienia uczelni ,był Jan Śniadecki."Jeżeli Kołłątaj był sercem reformy Akademii Krakowskiej, to Jan Śniadecki był jej mózgiem" - pisze historyk matematyki polskiej - S.Dickstein. J.Śniadecki urodził się w Żninie koło Gniezna 29 sierpnia 1756 roku. Po siedmiu latach nauki w Kolegium Lubrańskiego w Poznaniu, w roku 1772, przybył do Krakowa, a w trzy lata później otrzymał stopień doktora filozofii Uniwersytetu Krakowskiego. Upoważniło go to do prowadzenia wykładów z algebry, dzięki którym zwrócił na siebie uwagę Kołłątaja i zdobył uznanie całego uniwersytetu. Zapewne w dowód tego uznania został mianowany nauczycielem w tzw. Szkołach Nadworskich - zakładzie ściśle związanym z Akademią Krakowską. Wykładał tu ku zadowoleniu władz szkolnych różne
przedmioty, również takie, których nie studiował w Akademii;było to oczywiście możliwe dzięki wytężonej pracy nad sobą. W roku 1778 wyjechał na własny koszt (później korzystał również z prywatnej pomocy Kołłątaja i Komisji Edukacyjnej)na studia zagraniczne. Przebywał kolejno w Niemczech (Getynga),Holandii (Lejda)i Francji (Paryż). Na uniwersytecie w Getyndze borykał się początkowo z trudnościami, które charakteryzuje: "Rzuciłem się do prywatnego uczenia i czytania z największym zapałem;tłumaczenia i wyjaśnienia profesorów nie zawsze mogły mnie zaspokoić. Wszelako postępowałem coraz dalej przy najuporczywszej pracy a moje pojęcie zaczęło się coraz bardziej rozjaśniać". Swe wykształcenie matematyczne pogłębił w College de France w Paryżu;poznał tu również gruntownie chemię ,fizykę i literaturę francuską. Uczonego Polaka - "arcykapłana umiejętności na całą Polskę i Litwę" oczekiwano w kraju. W roku 1781 po odrzuceniu propozycji D`Alamberta objęcia posady astronoma w Madrycie wraca do Krakowa i z nowym rokiem
akademickim obejmuje katedrę matematyki,w rok później wykłada też astronomię. Jego pierwszy wykład "O nauk matematycznych początku,znaczeniu i wpływie na oświecenie publiczne" wywarło olbrzymie wrażenie na studentach i profesorach. Jan Śniadecki, widząc niższy poziom matematyki w Polsce niż u innych narodów, postanowił przyczynić się do poprawy tego stanu rzeczy. Zaczął od opublikowania podręczników uniwersyteckich, w których zawarł nowe treści, kształtując równocześnie polską terminologię matematyczną. Zagadnieniu terminologii matematycznej poświęcił osobną rozprawę "O języku narodowym w matematyce". Zawierała ona oprócz ogólnych rozważań konkretne propozycje terminów matematycznych. Los ich był rożny: jedne z nich wyszły z użycia, inne uległy przekształceniu, a inne przetrwały do dziś. Przykładem może być polski termin "całka" jako odpowiednik terminu integrał. Najbardziej znaną pracą Śniadeckiego jest doskonały podręcznik geometrii analitycznej i algebry wyższej: "Rachunku algebraicznego teoria
przystosowania do linii krzywych". "Trygonometria sferyczna analitycznie wyłożona" (tłumaczona na język niemiecki) jest jak gdyby do niej dodatkiem. Do najważniejszych prac Śniadeckiego poza wymienionymi należy rozprawa o Koperniku, będąca pierwszym poważnym studium o dziele twórcy nowoczesnej astronomii. Zasługi J.Śniadeckiego dla rozwoju nauki polskiej są niewątpliwie duże, ale bardziej wyraźne w dziedzinie organizacji nauki i nauczania niż ściśle naukowej. Właśnie J.Śniadecki, dzięki ważkości swych argumentów, odsunął prośbę zamknięcia bądź przeniesienia Uniwersytetu Krakowskiego do Warszawy. On również, będąc rektorem, poważnie przyczynił się do rozwoju Uniwersytetu Wileńskiego. Namiętne oddanie się sprawom społecznym prawie całkowicie wypełniało jego czas i nie pozwoliło zrealizować marzeń z młodości - twórczego udziału w rozwoju wiedzy, szczególnie matematyki i astronomii. Według Śniadeckiego, "matematyka jest królową wszystkich nauk, jej ulubieńcem jest prawda, a prostość i oczywistość jej strojem.
Ale przybytek tej monarchini jest obsadzony cierpieniem, po którym przechodzić trzeba". Jan Śniadecki wyróżniał się "charakterem nadto żywym ,nie dość cierpliwym i do rozdrażnia łatwym" (jego własne słowa),cechowała go wytrwałość w dążeniu do celu;nie znosił sprzeciwu. Ostatni okres życia (od 1825 roku) spędził w Jaszunach. Umarł 9 listopada 1830 roku. Powrót
JEAN BAPTISTE JOSEPH FOURIER(1768-1830) : Jan Chrzciciel Józef Fourier - wielki francuski matematyk - urodził się 21 marca 1768 roku w Auxerre w rodzinie krawca. W 18 roku życia zostaje sierotą i wówczas korzystając z pomocy jednego z przyjaciół zapisuje się do szkoły wojskowej w swoim rozinnym mieście. Tu wkrótce wyróżnia się jako student,robiąc szybkie postępy w nauce, szczególnie w matematyce. Z powodu ubóstwa i pochodzenia nie ma szans na dalszy awans, dlatego też po ukończeniu szkoły (1784) zostaje w niej jako wykładowca matematyki. Prowadzi także wykłady z historii i retoryki. W 1796 r. Fourier wyjeżdża do Paryża i tu obejmuje katedrę analizy w Szkole Politechnicznej. W okresie kampanii Napoleona w 1798 wraz z innymi uczonymi towarzyszy Bonapartemu do Egiptu, gdzie zostaje gubernatorem Dolnego Egiptu. Przez 3 lata był sekretarzem Instytutu w Kairze, ufundowanego przez Napoleona. Instytut ten zawdzięcza swój rozwój Fourierowi. W 1801r. wraca do Francji i w
następnym roku obejmuje stanowisko prefekta departamentu miasta Isere, uzyskując tytuł barona, oraz zostaje odznaczony Orderem Legii Honorowej. Na tejże prefekturze pozostaje przez 14 lat. W tym okresie kieruje wydawnictwem "Description de l`Egipte" oraz prowadzi pracowite i owocne badania nad przewodnictwem ciepła. W 1815 roku po powrocie Napoleona z Elby, publikuje proklamację rojalistyczną ,za co zostaje pozbawiony prefektury w Isere a także przydzielonej mu zastępczo prefektury w Rodanie. Od 1817 r. poświęca się wyłącznie badaniom naukowym. Przenosi się do Paryża, gdzie zostaje wybrany do Akademii, ale wyniku opozycji Ludwika XVIII staje się jej członkiem dopiero rok później. Od 1827 zastępuje Piotra Laplace`a na stanowisku rektora Szkoły Politechnicznej. Fourier umiera 18 maja 1830 roku w Paryżu. Ogromnej wagi jego prace i badania zapewniły mu sławę światową. Jego metody sązupełnie oryginalne ,a teoria równań zawdzięcza mu wiele istotnych ulepszeń. Szeregi nazwane jego imieniem (szeregi Fouriera)
odegrały wielką rolę i są często stosowane. Fourier pracował nad teorią ciepła i analizą - szczególnie nad teorią funkcji, rachunkiem całkowym i nad równaniami różniczkowymi. Zasadniczym jednak obszarem jest zainteresowań była fizyka matematyczna. Już w roku 1807 i 1811 roku przedstawił Paryskiej Akademii Nauk swoje pierwsze odkrycia, a w `1822 roku opublikował pracę "Analityczna teoria ciepła". Praca ta była punktem wyjścia do stworzenia teorii szeregów trygonometrycznych i opracowania niektórych zagadnień analizy matematycznej. wynikiem prac Fouriera nad liczbowymi metodami rozwiązywania równań algebraicznych jest wydana już pośmiertnie (1831) "Analiza określonych równań". Powrót
SIMEON DENIS POISSON(1781-1840) :Ten wybitny fizyk i matematyk francuski urodził się 21 czerwca 1781 roku w Pithiviers (departament Loiret). W latach 1798-1800 kształcił się w Szkole Politechnicznej w Paryżu,po czym rozpoczął w niej pracę nauczycielską. W roku 1806 Poisson został profesorem Uniwersytetu Paryskiego. W tym czasie był jednym z najznakomitszych młodych matematyków. Od chwili ukończenia Szkoły Politechnicznej interesował się pewnymi zagadnieniami astronomicznymi, mechaniką teoretyczną oraz zastosowaniami matematyki w mechanice i fizyce. To ostatnie zainteresowanie doprowadziło go w latach późniejszych do odkryć w matematyce "czystej" . W roku 1811 wydał pierwsze poważne dwutomowe dzieło pt. "Traktat o mechanice". praca powyższa przez długi czas była jednym z lepszych podręczników mechaniki. Odznacza się jasnością wykładu i przystępnością mimo nasycenia zagadnieniami z fizyki, astronomii i balistyki. W roku 1812 Poisson zostaje członkiem Paryskiej
Akademii Nauk. W rok później ogłasza pracę "Uwagi o równaniach ciążenia", gdzie wyprowadza równanie nazwane później jego nazwiskiem. Prace Poissona - a ogłosił ich ponad 300 - obejmują różnorodne problemy, na przykład zagadnienie stałości systemu słonecznego, teorię sprężystości, hydromechanikę, elektrostatykę i magnetyzm. W czystej matematyce do dziś mają znaczenie prace na temat całki oznaczonej ,teorii równań różniczkowych o pochodnych cząstkowych i teorii rachunku prawdopodobieństwa. W roku 1816 Poisson objął katedrę mechaniki teoretycznej na Uniwersytecie Paryskim, gdzie pracował do roku 1837. W roku 1826 został przyjęty w poczet członków Petersburskiej Akademii Nauk. Z poważniejszych prac, jakie ogłosił w latach późniejszych, wymienić należy : "Memoire sur la theorie des ondes " ("Teorię fal" - 1826),"Theorie nouvelle de l`action capillaire" ("Nowa teoria włoskowatości" - 1831), "Theorie du calcus de probabilities" ("Teoria rachunku prawdopodobieństwa" - 1833) oraz "Theorie mathematique de la chaleur"
("Matematyczna teoria rozchodzenia się ciepła" - 1835). W oczach współczesnych Poisson stanowił typ solidnego człowieka. Jako stronnik Napoleona otrzymał od niego tytuł barona i wiele odznaczeń. Mimo to gorliwie służył i późniejszym po Napoleonie rządom Za Ludwika Filipa został w 1837 r. członkiem izby parów. Powrót
GEORGE GREEN(1793-1841) : Lata czterdzieste XIX wieku były dla matematyki angielskiej początkiem długo oczekiwanego ożywienia. Działalność matematyczna Hamiltona, Greena, Caylaya,Sylwestra, Salmona i innych wydała owoce, których jakość mogła konkurować wreszcie z równoległymi pracami matematyków na kontynencie. Wiele z tych prac miało charakter pionierski i do takich właśnie zaliczyły się osiągnięcia Greena. Urodzony w r 1793 w Seiton koło Nottingham, George Green wcześnie zainteresował się matematyką, kształcąc się początkowo samodzielnie. Podłożem tych zainteresowań stały się jednakże zagadnienia fizyczne, głównie zjawiska elektryczne i magnetyczne, które poza początkowymi wynikami Poissona nie posiadały własnej teorii. Marzeniem młodego Greena , który z zamiłowaniem czytał "Mechanikę niebieską" Laplace`a, było stworzenie podstawy matematycznej teorii zjawisk elektromagnetycznych. Wynikiem samodzielnych wysiłków Greena była "Próba zastosowania analizy
matematycznej w teorii elektryczności i magnetyzmu" ogłoszona w 1828 roku. Pracą tą Green dał początek metodom, które określamy mianem fizyki matematycznej. Ponadto stworzył wraz z Gaussem podwaliny teorii potencjału, rozwiniętej potem w nieomalże samodzielny dział matematyki. Sama nazwa "potencjał" pochodzi właśnie od Greena. Szereg jego dalszych prac, publikowanych już w czasie jego studiów w Caius Colledge w Camridge (1833-1837 ,jest rozwinięciem i zastosowaniem teoretycznym pierwszej pracy. Do najświetniejszych prac należą : "O odbiciu i załamaniu głosu", "O Odbiciu i załamaniu światła na wspólnej powierzchni dwu niekrystalicznych ciał" (grudzień 1837). Mimo świetnych sukcesów Green pozostał człowiekiem wielkiej skromności i taktu. Wybrany w r. 1839 "fellowship" w Caius Colledge. Green ze względu na stan zdrowia opuszcza uczelnię udając się do domu w Sneiton, gdzie wkrótce umiera mając 47 lat. Artykuł, "O przechodzeniu światła przez ciała krystaliczne" odczytany jeszcze przez autora, zamknął rejestr
prac człowieka, któy jako matematyk przewyższał swych kolegów zarówno na uniwersytecie ,jak poza nim. Powrót
JÓZEF HOENE-WROŃSKI(1778-1853) : W historii matematyki do koca XIX wieku należy wymienić trzech matematyków polskich, którzy wnieśli poważniejszy wkład w rozwój matematyki światowej :Adam Kochański, Jan Śniadecki i Józef Wroński. Najwybitniejszym z nich był Wroński. Uczony ten urodził się w Wielkopolsce, prawdopodobnie w Poznaniu, w roku 1778. Ojciec jego Hoene - Czech z pochodzenia - był człowiekiem wykształconym i zamożnym. W Wieku 15 lat Wroński ukończył Korpus Kadetów w Warszawie i otrzymał topień porucznika w artylerii narodowej. Wyróżnił się w walkach przeciwko oblegającym Warszawę Prusakom. Brał udzaiał w bitwie pod Maciejowicami,gdzie dostał się do niewoli. W 1795r. wstąpił do armii carskiej;służył w niej dwa lata w stopniu majora,później podpułkownika. Co skłoniło 17 letniego młodzieńca do tego kroku - nie wiadomo. Wiadomo natomiast,że na wieść o tworzeniu się Legionów Polskich wystąpił z armii rosyjskiej i wyjechał do Niemiec. W ciągu dwóch lat poznał
tu bujnie rozwijającą się wówczas filozofię niemiecką. I znów w roku 1800 obowiązek skłonił go do wyjazdu do Francji, by bogatą już wtedy swą wiedzę oddać na usługi dla kraju. Po krótkim pobycie w Paryżu wyjechał do Marsylii gdzie wstąpił do Legionu Polskiego. Pobyt w Marsylii duży wpływ na dalsze koleje jego losu. Hoene-Wroński odrzucił ostatecznie myśl o karierze wojskowej lub dyplomatycznej i postanowił poświęcić się pracy naukowej. Pracował w różnych gałęziach wiedzy. W Marsylii powstały pierwsze jego prace naukowe, tu powstały zarysy jego przyszłych pisanych wyłącznie po francusku prac zmierzających do zreformowania ludzkiej wiedzy. Zaszczyty ,jakie go spotkały ze strony miejscowego środowiska kulturalnego (został członkiem -korespondentem towarzystwa naukowego Marsylii, tzw. Akademii, oraz sekretarzem generalnym Towarzystwa Lekarskiego) nie zaspokoiły ambicji Wrońskiego. Postanowił wystąpić na szerszą widownię. W tym celu w drugiej połowie roku 1810 wyjechał do Paryża, gdzie pomijając krótkie
wyjazdy do Anglii, Belgii i Niemiec,zamieszkał na stałe. Odtąd jego życie jest całkowicie wypełnione pracą. "Żelazna jego natura - pisze Dickstein w ponad 300 stronicowej biografii o Wrońskim - wymagała niewiele snu i pożywienia, do pracy zasiadał od wczesnego ranka i dopiero po kilkugodzinnym zajęciu przyjmował skromny posiłek mówiąc:"Dzień swój zarobiłem"".Pozostawił ogromną ilość prac z matematyki, filozofii,fizyki i nauk technicznych. Gdy po śmierci grono jego przyjaciół czyniło próby ogłoszenia drukiem wszystkich jego dzieł (wiele pozostało w rękopisach), to okazało się ,że stanowiłyby one dziesięć 800 stronicowych tomów. W trzynaście lat po śmierci Wrońskiego Towarzystwo Nauk Ścisłych w Paryżu, którego celem było skupienie polskich sił narodowych, rozpisało konkurs na ocenę jego prac. Wśród przyczyn ,że na rozpisany konkurs zgłoszono tylko jedną pracę ,że dzieła Wrońskiego poza skromnym gronem jego wielbicieli nie cieszyły się powodzeniem, należy wymienić obok nie uwzględnienia osiągnięć ówczesnych
matematyków i utrudnionej czytelności (z powodu nadmiernej ilości uogólnień oraz łączenia pojęć natury matematycznej i filozoficznej)również,cechujący Wrońskiego, nieprzyjemny, bezwzględny kult własnych tez, kult wykluczający wszelka krytykę. warto zaznaczyć ,że za swego życia nie spotkał się z krytyką ,która poza wskazaniem momentów niejasnych,może nawet niezbyt ścisłych w jego pracach,wyłowiłaby również pomysły naprawdę genialne. Imię Hoene-Wrońskiego trwale zapisało się w teorii równań różniczkowych;zwróciło po raz piewszy uwagę na wyznacznik funkcyjny, odgrywający podstawową rolę w teorii równań różniczkowych zwyczajnych liniowych. Wyznacznik ten został na jego cześć został nazwany wyznacznikiem Wrońskiego. Życie Wrońskiego było długie (umarł 9 sierpnia 1853 r w Paryżu) ale i trudne. Był taki okres ,ze dla ratowania chorej żony zmuszony był sprzedać własne buty. Na krótko przed zgonem snuł jeszcze plany swych prac, a kilka dni przed śmiercią, przeczuwając ,że się zbliża - rzekł : "Boże..ja miałem
tyle jeszcze do powiedzenia". Powrót
CARL FRIEDRICH GAUSS(1777-1855) :Twórczość naukowa może być różnej wartości;szczególnie cenna jest taka, która wyznacza nowe kierunki badań, nowe drogi, po których kroczą następcy. Do takiej należy twórczość genialnego niemieckiego matematyka Karola Fryderyka Gaussa. Urodził się 30 kwietnia 1777 r. w Brunszwiku w ubogiej rodzinie robotnika sezonowego. Studia uniwersyteckie odbył w latach 1795-1798 w Getyndze .Stopień naukowy doktora uzyskał w Helmstad w roku 1799 za tezę, w której podał ścisły dowód zasadniczego twierdzenia algebry, mówiącego, że każde równanie algebraiczne stopnia n o współczynnikach rzeczywistych posiada dokładnie n pierwiastków. W późniejszym okresie (w roku 1814 i 1850) podał jeszcze dwa inne dowody. Warto zaznaczyć ,że dowody tego twierdzenia podawane przed Gaussem, przez D`Alamberta, Eulera , Lagrange`a i Laplace`a nie były poprawne. W roku 1807 Gauss objął katedrę matematyki i jednocześnie funkcję dyrektora obserwatorium astronomicznego
w Getyndze. Pozostał tu aż 22 lutego 1855 roku , tj. do śmierci. Życie Gaussa przypadło na okres szczególnie burzliwy (najazd Napoleona na Niemcy, francuska rewolucja burżuazyjna, Wiosna Ludów 1848 r.)Żył jednak on poza nawiasem wydarzeń społecznych i politycznych. Poświęcił się w zupełności pracy naukowej, której wyniki są tym dla matematyki i innych pokrewnych gałęzi wiedzy, czym wydarzenia jego epoki dla historii. Jedną z cech charakteryzujących dorobek naukowy Gaussa, poza wspomnianą już na początku,jest jego wszechstronność. Zajmował się algebrą wyższą, teorią liczb,geometrią różniczkową, rachunkiem prawdopodobieństwa, teorią przyciągania, teorią elektryczności i magnetyzmu, zagadnieniami włoskowatości, geodezją i astronomią. W każdej z tych dziedzin pozostawił trwały dorobek. Pierwszym poważniejszym dziełem Gaussa są "Arytmetyczne badania".Zawiera ona prace z teorii liczb i wyższej algebry oraz interesującą teorię równania podziału koła tj. równania xn = 1 i związek między nimi a możliwości
przy pomocy cyrkla i liniału wielokątów foremnych. Wykazał mianowicie ,że jeżeli liczba boków wielokąta foremnego jest liczbą pierwszą postaci (22n + 1) to konstrukcja taka jest możliwa. Sam wykonał konstrukcję 17-kąta. DO ustalenia tego rozwiązywał dużą wagę. Wyrazem tego były życzenia, by na jego nagrobku wyryto 17-kąt foremny wpisany w okrąg. Na pomniku wzniesionym w Brunszwiku ku jego czci widnieje siedemnastokąt foremny. Na polu matematyki wyniki o nieprzemijającej wartości osiągnął w takich jej działach (poza wymienionymi),jak geometria różniczkowa, szeregi (szereg hipergeometryczny), funkcje eliptyczne. Gauss uważany jest również za współtwórcę geometrii nieeuklidesowej. Stosował teorię liczb zespolonych do rozwiązywań zagadnień. Sam termin "liczba zespolona" należy do Gaussa. Nie mniejsze zasługi niż dla matematyki położył Gauss w dziedzinie astronomii. Podstawowym jego dziełem z tego zakresu jest "Teoria ruchu ciał niebieskich". Wyłożył w nim teorię wyznaczania orbit planet na
podstawie ich obserwacji;stosował z powodzeniem metodę najmniejszych kwadratów. Jako znakomity astronom dał się poznać przy odnalezieniu planetoidy Ceres, odkrytej następnie przez Piazziego z Palermo. To co nie udało się innym matematykom, udało się Gaussowi; na podstawie obserwacji uzyskanych przez odkrywcę wyznaczył eliptyczny tor planetoidy. Wyznaczenie toru pozwoliło znowu ujrzeć zagubiony obiekt. Liczne są zasługi Gaussa w fizyce. Oprócz dorobku teoretycznego wzbogacił ją nowymi przyrządami. Na polu fizyki współpracował z W.Webebrem. Wynikiem tej współpracy było skonstruowanie w 1833 r. pierwszego w Niemczech telegrafu elektromagnetycznego. Należy stwierdzić ,że Gauss, mimo wspaniałych osiągnięć w wielu dziedzinach wiedzy, był matematykiem przed wszystkim. W jego życiu można wyróżnić okresy, kiedy pracował w pokrewnych matematyce gałęziach, ale i wtedy nie zaniedbywał matematyki, i to zarówno stosowanej jak i czystej. W skorowidzach nazwisk umieszczonych w książkach o treści matematycznej przy nazwisku
Gaussa widnieje długi szereg liczb, bo liczne są stronice, na których utrwalił się jego geniusz. Powrót
AUGUSTIN LOUIS CAUCHY(1789-1857) :Cauchy urodził się 21 sierpnia 1798 roku w Paryżu w chwili ogromnie doniosłej dla Francji., w kilka tygodni po wybuchu wielkiej rewolucji francuskiej;był synem prawnika. Po ukończeniu Szkoły Politechnicznej w 1807 roku i Szkoły Budowy Dróg i Mostów w 1810 z polecenia rządu pracował jako inżynier przy pracach portowych. Zapewne musiał wtedy wiele czasu wolnego poświęcić królowej nauk, skoro już w 1811 przedstawił Akademii Paryskiej pracę z teorii wielościanów, którą zwrócił na siebie uwagę uczonych. Dość szybko zdobył rozgłos i osiągnął najwyższy zaszczyt: fotel w Akademii Paryskiej (1816);poza tym prowadził wykłady w College de France, w Sorbonie i w Szkole Politechnicznej. Fotel w Akademii zapewniła mu praca konkursowa p.t "O rozchodzeniu się fal na powierzchni cieczy". w roku 1830 po rewolucji lipcowej, w wyniku odmowy złożenia przysięgi wierności nowemu rządowi, Cauchy wraz z rodziną opuścił Francję. Najpierw przebywał w
Szwajcarii, potem przez dwa lata w Turynie gdzie prowadził katedrę fizyki matematycznej (katedra ta została specjalnie dla niego założona). W roku 1833 udał się do Pragi;przez pięć lat zajmował się tam edukacją syna króla Karola X (w nagrodę nadano mu tytuł barona).Po powrocie do Francji (1838 r.) odzyskał utracone zaszczyty. W stosunku do niego uczyniono wyjątek: zezwolono mu wykładać, mimo ,że nie złożył przysięgi wierności ówczesnemu rządowi. Spis prac Cauchy`ego obejmuje ponad 800 pozycji. Okolicznością wielce sprzyjającą tej obfitości wyników było, poza pracowitością i genialnością jego umysłu, ich przychylne przyjmowanie przez współczesnych. W tym bogatym dorobku naukowym znajdują się prace różnego typu i z różnych dziedzin matematyki. Składają się na nie wyniki jego własnych badań, sprawozdania z prac nadsyłanych Akademii i wyniki pracy dydaktycznej - wspaniałe podręczniki analizy matematycznej, będące wzorem i szkołą myślenia naukowego dla następnych pokoleń matematyków. Prace Cauchy`ego dotyczą
analizy,geometrii, teorii liczb i fizyki matematycznej. W algebrze na przykład zawdzięczamy mu piękny dowód zasadniczego twierdzenia algebry; w teorii liczb wykazał ,że każda liczba naturalna jest już liczbą n-kątną, albo daje się przedstawić jako suma nie więcej niż n liczb n-kątnych; w fizyce matematycznej do niego należy najogólniejsze sformułowanie matematyczne pojęcia odkształcenia i napięcia sprężystego. Osobny, dominujący rozdział w twórczości naukowej Cauchy`ego stanowi analiza matematyczna wraz z funkcjami zmiennej zespolonej i teorią równań różniczkowych. Jego zasługą jest zebranie i uściślenie bogatego dorobku matematyków XVIII wieku. Konsekwentnie posługiwał się pojęciem granicy i wprowadzonej przez niego ciągłości funkcji. Takie pojęcia jak :"granica funkcji w sensie Cauchy`ego", "ciągłość funkcji w sensie Cauchy`ego","iloczyn Cauchy`ego szeregów", "kryterium Cauchy`ego zbieżności szeregów","metoda Cauchy`ego" (całkowania równań różniczkowych),"reszta Cauchy`ego", "twierdzenie Cauchy`ego
(i Penna)o istnieniu", "zagadnienie Cauchy`ego", "twierdzenie całkowe Cauchy`ego", "wzór całkowy Cauchy`ego","nierówność Cauchy`ego" - są w codziennym użyciu większości matematyków. W dziejach rachunku różniczkowego i całkowego (rozumianego w szerokim znaczeniu) i tym samym w dziejach matematyki A.L.Cauchy zajął trwałe, wybitne miejsce. Cauchy żył w ciekawym historycznie okresie dla Francji;sam jednak był anarchistą. Reprezentował kierunek katolickiego wychowania młodzieży. Powrót
NIKOŁAJ IWANOWICZ ŁOBACZEWSKI(1792-1856) : Pierwszym człowiekiem, który odważył się wystąpić z nową teorią geometrii, teorią całkowicie odmienną od jedynej i powszechnie uznawanej teorii Euklidesa, był rosyjski matematyk Nikołaj Iwanowicz Łobaczewski. Rozpoczął on nową epokę w tym dziale matematyki, zdobywając sobie zaszczytne miano "Kopernika geometrii" .Dokładna data jego urodzenia nie jest znana. Jedne źródła podają rok 1792, inne 1793. Ojciec jego, urzędnik w Niżnym Nowogrodzie, zmarł wkrótce po jego urodzeniu. Jedynie dzięki niezwykłej ofiarności matki ukończył Łobaczewski wraz ze swymi dwoma braćmi gimnazjum w Kazaniu. Wstąpił następnie na dopiero co otwarty prowincjonalny Uniwersytet Kazański, którego profesorowie rekrutowali się przeważnie z krajów Europy Zachodniej. Już na pierwszym roku studiów młody Łobaczewski wyróżnia się niezwykłymi zdolnościami. Zwraca na siebie uwagę profesora Bartelsa, który osobiście zaopiekował się tym nieprzeciętnym
studentem. Tak opieka była Łobaczewskiemu konieczna, ponieważ swoimi psotami i bezbożnością wywoływał ogólne niezadowolenie. Opinia Bartelsa - mówią za ,że "Łobaczewski jako student ma tyle osiągnięć, iż na każdym z niemieckich uniwersytetów byłby prymusem..." przedstawiona senatowi - uchroniła przyszłego naukowca przed wydaleniem z uczelni. W 1811 Łobaczewski kończy studia i zostaje asystentem Bartelsa. Po trzech latach pracy awansuje na adiunkta. Chce w tym czasie wydać drukiem swoją pierwszą pracę pt. "Geometria", która jednak przeleżała w archiwu przeszło 70 lat ,gdyż nikt z członków Akademii jej nie zrozumiał. W roku 1816 został mu nadany tytuł profesora. W latach 1829-1840 Łobaczewski ogłasza kilka prac m.in. "Nowe podstawy geometrii z pełną teorią równoległych", w której przyjmuje swój słynny pewnik ,że przez dany punkt leżący na tej samej płaszczyźnie co dana prosta można przeprowadzić nieskończenie wiele prostych nie przecinających danej. Proste zawarte sąw kącie, którego ramiona nazwał prostymi
równoległymi do danej prostej. Pewnik Euklidesa głosi, że przez taki punkt przeprowadzić można tylko jedną prostą równoległą. Łobaczewski wybrany został dziekanem wydziału matematyczno-fizycznego;godność tę sprawował przez pięć lat. Był też przez 10 lat bibliotekarze uniwersyteckim. Założył gabinet fizyczny i obserwatorium astronomiczne. Z jego inicjatywy ukazały się"Notatki Naukowe Uniwersytetu Kazańskiego". W 1827 roku wybrano go rektorem i godność tą piastował przez 20 lat. Założył klinikę oraz rozbudował uniwersytet .Przez cały ten czas uczony pracował nad rozwinięciem swojej teorii geometrii, zajmując się również innymi działami matematyki. Między innymi opracował również metodę przybliżonego rozwiązywania równań algebraicznych n-tego rzędu. Zajmował się też rachunkiem prawdopodobieństwa. W 8146 roku minęło 30 lat pracy Łobaczewskiego jako kierownika katedry i zgodnie z obowiązująca wówczas w Rosji ustawą powinien był opuścić to stanowisko. Ale Senat z uwagi na jego zasługi zezwolił mu jednogłośnie
pozostać dalej na tym stanowisku. W kilka lat później Łobaczewski utracił wzrok i ostatnią swoją pracę "Pangeometria" dyktował. Nikołaj Łobaczewski umarł w 1856 roku, wierząc ,że jego nauka znajdzie zrozumienie i kontynuatorów wśród przyszłych pokoleń
. Powrót
JACOB STEINER(18.III.1796-1.IV.1863) :Syn szwajcarskiego rolnika, urodził się w 1796 roku w Utzedorf koło Solothurn. Z matematyką zetknął się jako samouk, szczególnie rozkochał w geometrii po zapoznaniu się z ideami Pestalozziego. W roku 1815 przeniósł się do Heidelbergu, gdzie dawał prywatne lekcje, które umożliwiały mu studia w Instytucie Pedagogicznym. W tym czasie uczył syna ministra Wilhelma non Humboldta. W 1834 minister i jego brat Aleksander, pragnąc ożywić idee Pestalozziego, sprowadzili Steinera do Berlina, gdzie utworzono dla niego katedrę. Został także członkiem Akademii Nauk. W Berlinie pracował aż do śmierci. Steiner był przedstawicielem geometrii syntetycznej ("czystej"). Według niego geometrię najlepiej można studiować przy pomocy skupionej myśli. Twierdził ,że liczenie zastępuje myślenie,geometria zaś je pobudza. Steiner położył ogromne zasługi na polu geometrii. Jego metody wzbogaciły ją w wiele pięknych i często skomplikowanych twierdzeń.
W twierdzeniach często opuszczał dowody, co uczyniło jego zebrane dzieła skarbem dla geometrów poszukujących problemów do rozwiązania. Przy pomocy jednej ze swoich metod, tzw metody czteroprzegubowej, wykazał w bardzo ciekawy sposób, że koło jest figurą o największej powierzchni wśród wszystkich figur płaskich ograniczonych krzywymi zamkniętymi w tym samym obwodzie. Zajmował się też geometrią elementarną wykazując ,że wszystkie konstrukcje geometrii Euklidesa można wykonać za pomocą liniału,jeśli tylko w tej samej płaszczyźnie jest dany okrąg wraz ze swym środkiem. A oto ciekawa konstrukcja, tzw. konstrukcja Steinera, polegająca na tym ,by za pomocą samego liniału wykreślić prostą równoległą do danego odcinka, mając dany jego środek. Dane:odcinek AB, środek S odcinka AB i punkt P nie leżący na prostej AB. Wykreślić prostą równoległą do AB i przechodzącej przez punkt P. Konstrukcja: z punktu A prowadzimy półprostą przez punkt P. Na tej półprostej obieramy punkt C taki ,żeby nie leżał na odcinku AP,
następnie łączymy punkt C i S . P z B oraz C z B .W przecięciu odcinków PB i CS otrzymujemy punkt M. Przez punkt A i M prowadzimy prostą ,która przetnie odcinek CB w punkcie D. Przez punkt P i D prowadzimy szukana prostą równoległą do AB. Powrót
NIELS HENRIK ABEL(1802-1829) :Zachęcony przez swego nauczyciela Niels Henryk Abel próbował rozwiązać ogólne równanie algebraiczne stopnia wyższego niż 4. Początkowo sądził ,że udało mu się jako pierwszemu rozwiązać ten od dawna nurtujący wielu matematyków problem. Kiedy jednak znalazł błąd w swym rozwiązaniu, wpadł na rewelacyjny wprost pomysł,aby spróbować udowodnić ,że rozwiązanie takiego równania jest niemożliwe. Tym razem próba zakończyła się wielkim sukcesem 24 letniego wówczas młodzieńca. Udowodniona przez Abela niemożliwość rozwiązania ogólnego równania algebraicznego stopnia wyższego niż 4 przez pierwiastkowanie - to ustanowienie nowego i prowadzącego wreszcie do właściwego celu drogowskazu na drodze rozwoju współczesnej algebry. Abel był niewątpliwie jednym z najbardziej wydajnych matematyków XIX wieku. Urodził się w 1802 roku w Findoe w Norwegii jako drugi z siedmiu synów pastora. Jego krótkiemu, lecz ciężkiemu życiu towarzyszyła skrajna nędza,
niedocenianie zasług i brak zrozumienia u będących ówcześnie u szczytu sławy matematyków. Na świetnie zapowiadającego się młodego matematyka nie zwrócił uwagi nawet sławny Gauss, któremu Abel posłał dowód swojego słynnego obecnie twierdzenia. Z podobną obojętnością spotkał się Abel, jeszcze wciąż pełen optymizmu, w czasie pobytu w Paryżu (w 1824 r) ze strony słynnych matematyków francuskich. Przedstawiona Paryskiej Akademii Nauk jego praca została uznana i opublikowana dopiero po jego śmierci. Szereg swoich prac publikował Abel w czasopiśmie matematycznym wydawanym w Niemczech przez Crelle`a. Badani naukowe, które rozpoczął w dziedzinie algebry, przeniósł następnie na te dziedziny rachunku całkowego, które najbardziej były związane z algebrą Analogicznie do wspomnianego twierdzenia z dziedziny algebry udowodnił w dziedzinie rachunku całkowego niemożliwość całkowania wielu funkcji przy pomocy funkcji elementarnych. Badani te doprowadziły go do odkrycia funkcji eliptycznych i hiper eliptycznych. Całki tych
funkcji są szczególnym przypadkiem tzw. obecnie całek Abela (całki funkcji algebraicznych) i znajdują wielkie zastosowanie (np. w teoretycznej fizyce współczesnej). Szereg ważnych i nowych prac napisał i opublikował Abel również z teorii szeregów. Jedno z podstawowych twierdzeń w tej dziedzinie, twierdzenie o zbieżności szeregów jest znane jako twierdzenie Abela. Niestety,wszystkie publikacje i przedstawione zagranicznym akademiom prace pozostawały bez echa. Po powrocie do kraju Abel musiał zarabiać an życie korepetycjami i z tej niewielkiej sumy utrzymywać owdowiałą matkę wraz z młodszym rodzeństwem. Dopiero w 1828 roku udało mu się otrzymać skromne stanowisko na uniwersytecie. Warunki materialne jednak tak głęboko odbiły się na zdrowiu ,że w 1829 roku,mając zaledwie 27 lat zmarł na gruźlicę. Tymczasem w drodze do niego był list z propozycją objęcia katedry w Berlinie. List ten nie zdążył dotrzeć do jego rąk. Powrót
EWARISTE GALOIS(1811-1832) : Około roku 1830 na firmamencie matematyki zabłysła nowa gwiazda niesłychanej jasności Ewaryst Galois. Tymi słowami określił znany matematyk niemiecki Feliks Klein pojawienie się prawdziwego geniusza matematycznego,który mimo swego niezwykle młodego wieku (zginął tragicznie, nie mając ukończonych 21 lat) doszedł do wyników gwarantujących mu trwałą pozycję twórcy podstaw współczesnej algebry. Galois urodził się w Bourg-la Reine koło Paryża. Ojciec jego był nauczycielem szkoły podstawowej. W 1823 roku opuścił dom rodzinny, by rozpocząć naukę w klasie czwartej Liceum Ludwika Wielkiego. Mając 15 lat przypadkowo zainteresował się nieobowiązkową w klasie retoryki matematyką i już w kilka tygodni po przeczytaniu geometrii Legendre`a zaczął formułować własne poglądy. W roku 1824 norweski matematyk Niels Henryk Abel udowodnił ,że niemożliwe jest rozwiązanie przy pomocy pierwiastków dowolnych równań algebraicznych stopnia wyższego niż
czwarty. Galois jako 17 letni uczeń nie tylko samodzielnie doszedł do tego rezultatu,ale postawił problem, jeden z najtrudniejszych w matematyce w ogóle, a najdonioślejszy w dziedzinie algebry. Polegał on na znalezieniu kryterium dającego odpowiedź na pytanie, czy równanie algebraiczne danego stopnia daje się rozwiązać przy pomocy pierwiastków. Galois jako uczeń debiutował naukowo na łamach czasopisma matematycznego, w znacznie zaś obszerniejszej pracy sformułował wyniki swoich badań i przesłał je Akademii Nauk. Niestety rękopis ten, zawierający bezspornie najgenialniejsze idee stulecia, zaginął. trudno sobie wyobrazić, że Galois dwukrotnie nie zdał egzaminu wstępnego z matematyki do Szkoły Politechnicznej. W odpowiedziach na zbyt łatwe pytania ograniczał się do zwięzłych, logicznych tak zrozumiałych dla niego stwierdzeń ,że odmawiał szerszego objaśnienia. W 1830 roku Galois rozpoczął studia w l`Ecole Normale, lecz po upływie roku został wydalony za zdemaskowanie w prasie dwulicowej roli dyrektora szkoły w
czasie przewrotu lipcowego. Po wstąpieniu na tron Ludwika Filipa Galois bierze aktywny udział w walce politycznej, należąc do lewicowego republikańskiego stronnictwa "Przyjaciół Ludu". Za publiczne wystąpienia przeciwko reżimowi królewskiemu dwukrotnie przebywał w więzieniu. Tam też otrzymał pismo z Akademii Nauk, odpowiedź na powtórnie wysłany rękopis. Wybitny matematyk Poisson któy referował tą pracę,, opatrzył ją następującą uwagą"..nie jesteśmy nawet w stanie uchwycić myśli przewodniej autora". Prawie bezpośrednio po odzyskaniu wolności Galois zginął w pojedynku, sprowokowanym przez politycznych przeciwników. Galois pracował głównie nad rozwiązywalnością równań algebraicznych. Wybitnym osiągnięciem było znalezienie warunku koniecznego i dostatecznego, który spełniają równania danego stopnia rozwiązywalne przez pierwiastkowanie. Aby dojść do tego rezultatu Galois stworzył zupełnie nową teorię (teoria grup - zwana także teorią Galois), wprowadzając do niej szereg fundamentalnych pojęć. Teoria grup
zdecydowanie wpłynęła na rozwój nie tylko algebry, ale i całej dziewiętnastowiecznej matematyki, a idee i metody teorii grup znajdują wciąż nowe i ważne zastosowania. Powrót
KARL GUSTAW JAKOB JACOBI(1804-1851) :Karl Gustaw Jakub Jacobi urodził się w Poczdamie jako syn berlińskiego bankiera. Jego starszy brat był znanym i cenionym fizykiem, profesorem w Petersburgu. Matematyką zainteresował się bardzo wcześnie. Jej też poświęcił wiele uwagi w szkole średniej, po której ukończeniu rozpoczął studia matematyczne w Berlinie. Jego kariera naukowa była wprost błyskawiczna. Jesienią 1825 roku, mając zaledwie lat 21 Jacobi otrzymuje tytuł doktora. Wiosną następnego roku wyjechał do Królewca, gdzie rozpoczął pracę na Uniwersytecie. Zyskał sobie powszechną opinię dobrego pedagoga. Jednocześnie stale pogłębiał swą wiedzę matematyczną. W Królewcu otrzymał tytuł docenta, a w rok później (1827) profesora nadzwyczajnego. W 1835 kiedy ukończył 31 rok życia, Karol Jacobi zdobył tytuł profesora zwyczajnego. W 1836 został członkiem Berlińskiej Akademii Nauk. Jacobi jest jednym z twórców teorii funkcji eliptycznych. Uczony ten odkrył szereg praw z
teorii liczb, algebry liniowej, badał równania różniczkowe z dynamiki, zajmował się równaniami pierwszego rzędu z pochodnymi cząstkowymi. Pracował nad wieloma zagadnieniami matematycznymi. Trudno było znaleźć gałąź ówczesnej matematyki, w której nie byłoby jakiegoś wkładu Jacobiego. Główne jego dzieło to "Fundamenta novae theoriae functionum ellipticarum". Mimo młodego wieku był znanym i cenionym wykładowcą. Jacobi interesował się również polityką. Początkowo należał do zwolenników króla, później jednak opowiedział się ,choć nigdy zdecydowanie, po stronie rewolucjonistów. Jacobi w swej pracy naukowej podejmował na nowo szereg problemów porzuconych przez Gaussa,Lagrange`a .Dokończył np. tablice dotyczące równości Xn = A, którą Gauss wykonał tylko dla liczb w zakresie do 89. Jacobi rozszerzył ją na wszystkie liczby w zakresie do 1000. Kontynuował on rozpoczęte przez Lagrange`a zagadnienia dotyczące równań podziału okręgu oraz prace Gaussa z zakresu teorii liczb. W 1829 roku Jacobi rozpoczął pracę nad
teorią funkcji analitycznych. W 1834 opublikował swe osiągnięcia dotyczące form kwadratowych. Interesował się także prawami zachodzącymi w zbiorze liczb całkowitych. Jego pomysłem było przedstawienie każdej liczby jako sumy kwadratów liczb całkowitych. Starał się zastosować teorię funkcji eliptycznych do geometrii analitycznej,na przykład przy pomocy całki eliptycznej przekształcił konforemnie elipsoidę na płaszczyznę. Bardzo intensywna praca naukowa szybko wyczerpała młody organizm. W 1843 roku Jacobi opuszcza Królewiec i udaje się na leczenie do Włoch. Stamtąd wyjechał do Berlina. Pracował jeszcze tylko kilka lat. 18 lutego 1851 roku umarł w Berlinie na ospę. Zbiór wszystkich jego prac wydała Akademia Berlińska w 8 tomach w latach 1881-1891. Powrót
MICHAIŁ WASILJEWICZ OSTROGRADZKI(1801-1861) :W historii matematyki jedno z poczesnych miejsc zajmuje rosyjski uczony - Michał Ostrogradzki. Lotny umysł. szerokie wykształcenie matematyczne i przyrodnicze pozwoliły mu uzyskać rezultaty o pierwszorzędnym znaczeniu w mechanice ii różnych działach matematyki. Nazwisko jego było szeroko znane poza granicami kraju. Najbardziej wymownym faktem jego sławy jest to ,że był członkiem Akademii Nauk - Rosyjskiej, Turyńskiej, Rzymskiej, Amerykańskiej i Francuskiej. Sława tego uczonego była w Rosji tak wielka,że gdy młodzi ludzie nie chcieli się uczyć, rodzice przekonywali ich słowami: "Ucz się a będziesz Ostrogradzkim". Michał OStrogradzki urodził się w 1801 roku w rodzinie bogatego właściciela ziemskiego w guberni połtawskiej. Nie ukończył gimnazjum, gdyż ojciec jego wyobrażał sobie ,że tak potężnie zbudowany chłopak musi poświęcić się karierze wojskowej. 15 letniego Ostrogradzkiego zawiózł ojciec do Petersburga, aby
zapisać go do pułku gwardyjskiego. Po drodze ,dzięki silnym namowom rodzin zmienił zamiar i młody Michał wstąpił na Uniwersytet Charkowski. Uczył się początkowo słabo, gdyż sam marzył o karierze oficera. Dopiero gdy zamieszkał u profesora matematyki Pawłowskiego, zaczął pod jego wpływem interesować się bardziej nauką i wkrótce stał się jednym z najlepszych studentów, celując szczególnie w matematyce. Jednak gdy w 1820 roku zdał wszystkie egzaminy końcowe z wynikiem bardzo dobrym, władze uczelni nie wydały mu dyplomu, motywując to wolnomyślicielstwem Ostrogradzkiego. Wyjechał wówczas do Paryżą i tam uczęszczał na wykłady Ampere`a, Cauchy`ego, Laplace`a. Poissona i innych. Wkrótce sam spróbował swoich sił w matematyce i za obliczenia szczególnie trudnych całek otrzymał od Cauchy`ego specjalną pochwałę. W 1825 roku wygłosił we Francuskiej Akademii pracę o rozchodzeniu się fal na powierzchni cieczy. W tym samym roku rozpoczął swoją pierwszą pracę pedagogiczną w College Henryka IV. W 1828 roku wrócił do Rosji.
Wykładał matematyk w Głównym Instytucie Pedagogicznym, w Korpusie Morskim oraz Michajłowskiej Szkole Artyleryjskiej. Wykłady Ostrogradzkiego odznaczały się niezwykle dokładnym przygotowaniem. Podawał w nich najnowsze osiągnięcia francuskich matematyków,nie znane jeszcze w Rosji. Był jednym z założycieli petersburskiej szkoły matematycznej. Publikował wiele prac z zakresu mechaniki teoretycznej, fizyk matematycznej, teorii liczb, algebry i rachunku prawdopodobieństwa. Ogłosił równanie różniczkowe z zakresu przechodzenia ciepła przez ciecze i ciała stałe. Podał wzór na przekształcenie całki objętościowej w całkę powierzchniową, znany studentom jako wzór Ostrogradzkiego. Wprowadził pojęcie zespolonego różniczkowego operatora. W pracy "O przekształceniach zmiennych w całkach ilorazowych" dał wyprowadzenie przekształcenia zmiennych całkowania w całkach podwójnych i potrójnych. Te dowody są obecnie podawane we wszystkich podręcznikach wyższej matematyki. Jako kryterium ważności prac matematycznych uznawał ich
zastosowanie w praktyce. Jedna z jego prac z rachunku prawdopodobieństwa o metodach statystycznych obliczania braków wynikła z zamiaru ułatwienia pracy sortowaczom towarów dostarczanych wojsku. Ostrogradzki umarł nagle w 1861 r. w Połtawie w drodze z domu do Petersburga. Powrót
JANOS BOLYAI(1802-1860) : Dwa tysiące lat to okes, któy pogrzebał wiele starych cywilizacji i dał życie wielu nowym. Od czasu Euklidesa przedstawia na swym marginesie historię pewnego geometrycznego postulatu, historię której bieg przyniósł w rezultacie nowe idee geometryczne, tak niepodobne do treści euklidesowych. Pewnik Euklidesa ,bo właśnie o nim mowa, intrygował wszystkie pokolenia matematyków od czasów jego autora. Przez okres dwóch tysięcy lat usiłowano dać odpowiedź na następujące pytanie: Czy pewnik Euklidesa jest zależny, czy też nie od pozostałych aksjomatów geometrii, a w konsekwencji - czy można, czy też nie otrzymać go w formie twierdzenia? Od odpowiedzi na to pytanie zależała możliwość zbudowania nowej geometrii, różnej od euklidesowej, zawierająca jako aksjomat zaprzeczenie euklidesowego pewnika. Dopiero po tym długim okresie zdołano, z korzyścią dla rozwoju geometrii, pytanie to rozstrzygnąć .Odpowiedzi nadeszły jednocześnie z trzech stron :
z Rosji - od Łobaczewskiego, z Niemiec - od Gaussa , i z Węgier - od Bolyai`a. Historia tego Węgra jest szczególnie interesująca. Jest bowiem dramatem człowieka głęboko zaangażowanego w rozwój nowych, rewolucyjnych idei. Janos Bolyai urodził się w 1802 roku w Kolozsvar. Ojciec jego Wolfgang, profesor matematyki, strawił znaczną część życia nad wspomnianym dylematem,jednakże poważniejszych wyników nie osiągnął. Dlatego też przekonywał syna, by nie zajmował się tym problemem. Janos wszakże nie poszedł za radą ojca i już podczas swych studiów na Królewskiej Akademii Inżynieryjnej w Wiedniu zaczął poszukiwać właściwego rozwiązania. Zachowane rysunki , pochodzące z tego okresu, wskazują ,że młody Bolyai znalazł właściwą drogę. Akademia owa kształciła korpus inżynieryjny służby wojskowej, której pełnienie rozpoczął Bolyai w dwudziestym roku życia. W armii młody oficer dzielił swój czas pomiędzy obowiązki, pojedynki, grę na skrzypcach i matematykę. Kontynuując swe poszukiwania, już w 1825 roku doszedł do podstawowych
pojęć i twierdzeń geometrii nieeuklidesowej. Jednakże ich ścisłe dowody zabrały mu dalsze sześć lat pracy. Opracowawszy w końcu uzyskane wyniki, zamieścił je w formie dodatku do książki swojego ojca, wydanej w 1832 roku. Wykład owego dodatku, noszącego tytuł "Appendix scientiam spatii absolutu veram exhibens" odznaczał się skrajną zwięzłością i schematycznością,ale ze względu na przemyślenie kazego słowa i oznaczenia należy to dzieło do najpiękniejszych w literaturze matematycznej. Mimo swej wagi, ukazanie się pracy matematyka węgierskiego nie wzbudziło większego zainteresowania, poza jednym entuzjastycznym przyjęciem Gaussa. Bardziej jednak niż brak zainteresowania zabolało Bolyai`a oświadczenie Gaussa, jakoby ten posiadał podobne wyniki. Odtąd Bolyai będzie miał w podejrzeniu Niemca ,że ten wykorzystuje jego idee. Podejrzenia te były zupełnie bezpodstawne, czego dowodem jest jeden z listów Gaussa, w którym wyraża opinię o "Appendix scientiam spatii absolutu veram exhibens", pisząc : "Uważam tego młodego
geometrę von Bolyai za geniusza pierwszej wielkości". Silnie się odbiło na psychice Węgra jego niepowodzenie w premiowanym konkursie ogłoszonym w Lipsku w 1837 r. Bolyai nadsyła świetna pracę, poprzedzającą konstrukcję Hamiltona. Nie zyskuje jednak ona uznania w oczach jury. Mimo stanu głębokiej depresji Bolyai stawia sobie za zadanie zbudowanie uwolnionej od wszelkich wyobrażeń i opartej jedynie na logicznych przesłankach ogólnej geometrii. To ambitne zadanie nie mogło być w owym czasie rozwiązane. Trzeba było dalszych 50 lat, by otrzymać jego pozytywny wynik. Tymczasem pogłębiająca się depresja osiąga u Bolyai`a swoje dno po ukazaniu się w 1840 niemieckiego wydania pracy Łobaczewskiego zatytułowanej "Geometryczne rozważania w teorii prostych równoległych". Bolyai dochodzi do wniosku, że Łobaczewski to nie istniejąca osoba, za którą ukrywa się Gauss. Od tej pory Węgier nie publikuje niczego więcej o matematyce,umrze (rok 1860) pięć lat przedtem ,zanim jego idea uzyska powszechne uznanie
. Powrót
PETER GUSTAV LEJEUNE DIRICHLET(1805-1859) :Piotr Gustaw Dirichlet (właściwie Derichlet), jedne z największych matematyków niemieckich urodził się 13 lutego 1805 roku w Duren, prowincji nadreńskiej. Już w młodości (od 1822 r.)przenosisię do Paryża, gdzie zamieszkuje w domu generała Foy. Miał tam sposobność poznać wiele znakomitości naukowych, filozozfów i matematyków. W tym też czasie uczęszczał na wykłady w College de France i w Facultedes sciences oraz zagłębiał się w epokowe dzieło Gaussa : "Disquistiones arithmeticae", które nadało ścisły kierunek jego zainteresowaniom badawczym. W roku 1826 wraca do Niemiec i zostaje docentem prywatnym na Uniwersytecie Wrocławskim, a następnie przenosi się do Berlina. Tu jest kolejno docentem prywatnym (od 1829 r.)potem od 1831 profesorem zwyczajny na uniwersytecie. Jednocześnie wykłada w szkole wojennej. W roku 1855 zostaje powołany na Uniwersytet w Getyndze jako zastępca Gaussa. jego oryginalna twórczość naukowa dotyczy
przeważnie teorii liczb, teorii szeregów, rachunku całkowego i pewnych zagadnień z fizyki matematycznej. W roku 1825 pisze pracę "Memoire sur l`impossibilite", która przedstawiona Akademii Paryskiej zwróciła na niego uwagę i zapewniła mu imię świetnego matematyka. w pracy tej rozważa Dirichlet przypadek tzw. wielkiego twierdzenia Fermata dla n = 5 (Euler i Lagrange rozważali przypadki dla n=3 i n= 4). Następnie podał dowody twierdzenia Gaussa (dla reszt dwukwadratowych). W pracach tych wskazał wielką przydatność analizy i teorii funkcji analitycznych przy rozwiązywaniu problemów z teorii liczb. Znane jest w tej dziedzinie piękne jego twierdzenie, ze w każdym niekończonym postępie arytmetycznym, którego wyraz pierwszy i różnica są liczbami całkowitemu względnie pierwszymi, jest nieskończenie wiele liczb pierwszych. Zagadnienie to wcześniej stawiało matematykom trudności nie do przezwyciężenia. Podał pierwszy ścisły dowód zbieżności szeregów Fouriera, w rachunku wariacyjnym podał tzw. zasadę Dirichleta.
Prace te inspirowały innych matematyków, jak Riemman i Cantor,co doprowadziło do zupełnie nowych odkryć w tej dziedzinie. Badania i rozprawy swe ogłaszał w Journal de math. Crelle`a i Rozprawach Akademii. Wielkiego działa nie napisał, ale jego dorobek naukowy i wykłady przyczyniły się do rozwoju wiedzy matematycznej w Niemczech. Po jego śmierci wykłady z teorii liczb w opracowaniu Dedekinda stały się dziełem klasycznym. Umarł 5 maja 1859 roku w Getyndze. Powrót
BERNHARD RIEMANN(1826-1866) :Rozwój współczesnej matematyki zawdzięcza w olbrzymiej mierze swoje ukierunkowanie wielkiemu uczonemu niemieckiemu XIX wieku Bernhardowi Riemannowi. Riemann był synem wiejskiego pastora. Za namową ojca studiuje początkowo na Uniwersytecie w Getyndze teologię,lecz wkrótce jego skłonności i zainteresowanie do nauk ścisłych biorą górę i młody student poświęca się całkowicie matematyce. Słucha wykładów Gaussa, a następnie na Uniwersytecie Berlińskim wykładów tak doskonałych matematyków jak: Dirichlet, Jacobi, Steiner. Przede wszystkim Dirichlet stał się jego wychowawcą, nauczycielem ,przyjacielem. Wszystko to bardzo dodatnio wpływa na na rozwój zdolności twórczych Riemanna. W 1851 r. w Getyndze otrzymuje doktorat za rozprawę poświęconą teorii funkcji zespolonych, a w trzy lata później zostaje docentem prywatnym (oficjalnym ,choć nie opłacanym) po przedstawieniu dwóch prac "O przedstawieniu funkcji przy pomocy szeregu trygonometrycznego"
oraz "O hipotezach leżących u podstaw geometrii". Pierwsza z tych prac poświęcona była badaniom warunków Dirichleta rozwijalności funkcji na szereg Fouriera. Riemann rozwinął tu i uogólnił wyniki swego nauczyciela. Jego druga praca o geometrii może jeszcze silniej pchnęła rozwój myśli matematycznej i fizycznej na obecne tory. Autor sklasyfikował tu wszystkie istniejące rodzaje geometrii, łącznie z rodzącymi się już geometriami nieeuklidesowymi, oraz wykazał możliwość tworzenia dowolnych ilości nowych przestrzeni. Praca ta umożliwiła powstanie ogólnej teorii względności Einsteina. Riemann zostaje z kolei wykładowcą na Uniwersytecie w Getyndze. Na jego pierwszy wykład przyszło podobno osiem osób,ale na następne jeszcze mniej. Riemann miał bowiem początkowo trudności w prowadzeniu wykładów. Oto co pisze jednak po pewnym czasie:"...Moja początkowa nieśmiałość już trochę ustąpiła i przyzwyczaiłem się myśleć więcej o słuchaczach niż o sobie samym i czytać z ich twarzy, czy mogę iść naprzód, czy też muszę raz
jeszcze wyjaśnić zagadnienie..." Wkrótce nieśmiałość Riemanna ustąpiła całkowicie i dzięki jego starannym przygotowaniom do wykładów uzyskiwał coraz lepsze rezultaty w nauczaniu. W wykładach swoich korzystał często z wielu wyników, których nie opublikował. Po jego śmierci udało się jednak dzięki pilnym i długotrwałym staraniom zebrać notatki jego słuchaczy. W ten sposób powstał dodatek do zebranych prac Riemanna, wydany dopiero prawie czterdzieści lat po jego śmierci. Pewne pojecie o tym, jak wiele zdziałał na polu matematyki, może dać lista metod , twierdzeń i pomysłów noszących jego imię:twierdzenie Riemanna-Rocha o funkcjach algebraicznych, powierzchnie Riemanna, całka Riemanna, lemat Riemanna-Lebesgue`a o całkach trygonometrycznych, geometria Riemanna, hipoteza Riemanna, macierz Riemanna w teorii funkcji abelowych, funkcje zeta Riemanna, metoda Riemanna rozwiązywania cząstkowych równań różniczkowych typu hiperbolicznego i wiele, wiele innych. I mimo iż napisał on bardzo mało prac, a opublikował
jeszcze mniej, to jednak każda z nich była olbrzymiej wagi, bogata w nowe idee. Niestety gruźlica przecięła przedwcześnie jego tak cenne dla nauki życie. Powrót
KARL WEIERSTRASS(1815-1897): Karol Weierstrass urodził się 31 października 1815 roku w Westfalli, w okręgu Munster, we wsi Ostefeld. W przeciwieństwie do wielu wybitnych matematyków niemieckich pochodził z rodziny katolickiej. W 1829 roku , kiedy ukończył 14 lat, rodzice wysyłają go do gimnazjum w Padeborn. Uczy się dobrze,choć nie jest wyróżniającym się nawet z matematyki. W 1834 Weierstrass kończy gimnazjum i w tym samym roku przenosi się do Bonn. Tutaj zostaje przyjęty na studia prawnicze. Pracuje bardzo intensywnie, gdyż zaczyna go coraz bardziej interesować matematyka. Jej też poświęca w Bonn dokładne studia. Uczęszcza na wykład profesora Gudermanna. Nie składa jednak na razie żadnych egzaminów końcowych. W 1839 przenosi się do Munster. Kontynuuje studia matematyczne. Warunki materialne zmuszają go jednak do podjęcia pracy w szkole średniej. W 1841 roku Weierstrass kończy studia matematyczne. Uczony wybrał sobie temat pracy z dziedziny funkcji
eliptycznych, temat, który profesor Gudermann określił jako "stanowczo za trudny". Prof. Gudermann poznał się jednak na swoim uczniu. W swej opinii, którą przedstawił Komisji Egzaminacyjnej, wyrażał się o nim w samych superlatywach, a kiedy poznał ostatecznie wyniki pracy Weierstrassa, dopisał jeszcze do tej opinii :"jako równouprawniony wkroczył w szeregi ukoronowanych sławą wynalazców". Powyższy zwrot wydał się przewodniczącemu Komisji czczym pochlebstwem i nie znając wcale wyników pracy Weierstrassa, zdecydował się wykreślić ów fragment z opinii. I choć prof. Gudermann namawiał swojego ucznia do opublikowania tej pracy, Karol Wierestrass oddał ją do druku waz z innymi swoimi dziełami dopiero w 54 lata później, ale już jako "opromieniony sławą" mistrz w swojej dziedzinie. Od tego czasu właściwie datuje się samodzielna praca Weierstrassa nad wieloma zagadnieniami matematycznymi. W swej działalności naukowej, Weierstrass zajmuje się m.in. teorią funkcji analitycznej opartej na szeregach potęgowych, algebrze
liniowej. Teorię funkcji zmiennej zespolonej rozwinął Weierstrass do tego stopnia ,że dał właściwie zupełnie nowe podstawy tej dziedzinie. Znane jest jego twierdzenie o zbieżności szeregów. Jest zwolennikiem tzw. arytmetyzacji algebry, tzn. wyłączenia geometrii ze wszystkich dowodów algebry. Początkowo bardzo usilnie stara się ją urzeczywistnić, później częściowo porzuca. Weirstarss nigdy nie starał się sam znaleźć zastosowanie dla swych odkryć w mechanice. Prace te zlecał swoim uczniom i współpracownikom, m.in. Kowalewskiej,Szwarcowi, Mittag-Lefflerowi. Po otrzymaniu dyplomu Weierstrass nie porzuca pracy nauczycielskiej w szkole średniej. Jeszcze króko pozostaje w Munster, następnie przenosi się do Deutsch-Krone (obecny Wałcz, na Pojezierzu Pomorskim), gdzie przebywa w latach 1842-1848. W roku 1848 opuszcza to miasto i pracuje w szkole średniej w Braunsberdgu przez 7 lat tzn. do 1855 roku. W 40 roku życia Weierstrass otrzymuje tytuł profesora nadzwyczajnego. Wtedy dopiero, tzn w 1855 roku osiedla się na
stałe w Berlinie. Rozpoczyna tutaj pracę na uniwersytecie. Po 8 latach intensywnej działalności Weierstrass otrzymuje tytuł profesora zwyczajnego. Jego wykłady cieszyły się niesłychaną popularnością, był bowiem cenionym przez studentów wykładowcą. Pochłonięty całkowicie pracą naukową, Weierstrass nie publikował nigdzie swych osiągnięć. Dlatego też wiele twierdzeń znanych Weirestrassowi odkryto ponownie w latach późniejszych. Swiej długie życie Weierstrass wypełnił całkowicie pracą naukową poświęconą matematyce. W Berlinie, Wierestrass pracuje ponad 30 lat. Tutaj umiera 19 lutego 1987 roku, nie doczekawszy sięani jednego wydania swych prac. Jego rewelacyjne wyniki zostały opublikowane po raz pierwszy dopiero w roku 1898. Powrót
PAFNUCY LWOWICZ CZEBYSZEW(1821-1894) : W referacie wygłoszonym w październiku 1894 roku na posiedzeniu Rosyjskiej Akademii Nauk, w kilka dni po śmierci Czebyszewa, A.A.Markow powiedział : "26 listopada niespodziewanie zmarł P.L Czebyszew. Dla naszej Akademii jest to strata nie do zastąpienia.. Imię Czebyszewa jest nie mniej znane w Paryżu niż w Petersburgu. Już od dawna był on jednym z ośmiu zagranicznych członków Akademii Nauk, co jednocześnie określa go jako wybitnego geometrę, sławnego w całej Europie..." Nie ma w tym ani słowa przesady, gdyż
Czebyszew położył niecenione zasługi w rozwoju światowej nauki. Bogata tematyka jego pras nie straciła nic ze swej aktualności. Tematyką i sposobem rozwiązywania postawionych sobie zagadnień stworzył nową szkolę matematyczną, znaną w świecie naukowym jako Szkoła Czebyszewa lub Petersburska Szkoła Matematyczna. Do jej najwybitniejszych członków należeli Markow, Łapunow, Zołotariew i wielu innych. Tematyka prac Szkoły Czebyszewa to analiza matematyczna, teoria liczb, rachunek prawdopodobieństwa. Mało znana jest młodość Czebyszewa. Wiadomo ,że urodził się 14 maja 1821 roku w majątku ziemskim swego ojca w Ozatowie w guberni kałuskiej. Rodzice jego pochodzili ze starych szlacheckich rodzin. Po zdobyciu wykształcenia podstawowego w domu Czebyszew wyjeżdża do Moskwy, gdzie uczęszcza do gimnazjum. Jego nauczyciel matematyki Pogorielskij poznał nieprzeciętne uzdolnienia matematyczne Czebyszewa i namówił go do studiowania w tym kierunku. Podczas nauki na Uniwersytecie Moskiewskim największy wpływ na kształcenie się
indywidualności młodego talentu wywarli profesorowie Braschman i Jerszow. Po czterech latach studiów Czebyszew kończy uniwersytet jako kandydat nauk. W 1846 zyskuje tytuł magistra i przenosi się do Petersburga, gdzie obejmuje stanowisko adiunkta przy Katedrze Teorii Równań na Uniwersytecie. W 1849 roku uzyskuje stopień doktora za pracę pt. "Teoria porównań", w trzy lata później uzyskuje tytul profesora nadzwyczajnego, w 1860 profesora zwyczajnego, a w 1872 tytuł zasłużonego profesora. Równocześnie pracuje w Akademii Nauk i w 1859 roku zyskuje tytuł członka zwyczajnego Akademii .Czebyszew publikuje wiele prac naukowych. I tak zajmuje się teorią interpolacji i przybliżeniami funkcji,stosując w tych zagadnieniach wielomiany,zwane później wielomianami Czebyszewa. Jego prace z zakresu teorii liczb zapoczątkowały działalność Petersburskiej Szkoły Matematycznej. Zajmując się rachunkiem prawdopodobieństwa ogłasza słynną pracę dotyczącą pewnej nierówności, a noszącej do dziś nazwę nierówności Czebyszewa. W dalszych
pracach ogłasza słynne prawo wielkich liczb. Większość problemów, którymi się zajmował, cechuje ogromne powiązanie z praktyką. Rozwiązał wiele zagadnień z zakresu mechaniki, wytrzymałości materiałów i kartografii. Opublikował m.in. prace : "O kołach zębatych", "O rysowaniu map" i "O krojeniu ubrań". Wydawać się może , żę autor ich przestał interesować się matematyką, lecz Czebyszew pisząc np. "O krojeniu ubrań" uzasadnił praktyczne zastosowanie prawa o funkcjach. Właśnie ta olbrzymia praktyczna przydatność jego prac uczyniła nazwisko Czebyszewa sławnym w całym świecie. Powrót
CHARLES HERMIT(1822-1901) : Francuski matemtyk, urodził się 24 grudnia 1822 roku w Dieuze (Muerthe).Będąc jeszcze uczniem l`Ecole Politechnique w Paryżu ,ogłosił rozprawę o funkcjach Abelam a już w 1848 został repetytorem analizy matematycznej i egzaminatorem w tejże uczelni. W uznaniu za wybitne prace naukowe został w 1856 przyjęty do grona członków Akademii Nauk. W 1869 r, został profesorem tejże uczelni. Od 1870 roku mianowany profesorem nauk ścisłych w Sorbonie. Po śmierci Cauchy`ego w 1857 r. Hermite uważany był przez matematyków za czołowego analityka Francji. Prace Hermite`a dotyczyły głównie teorii liczb, funkcji eliptycznych, funkcji theta, teorii niezmienników i funkcji modularnych. Podał on rozwiązanie równania piątego stopnia za pomocą funkcji eliptycznych. Twórców teorii niezmienników, którymi byli Cayley, Sylwester i Hermite, nazywał on w swych listach "Trójką Niezmienników". W r. 1873 Hermite udowodnił że e jest liczbą przestępną
(transcendentną). Posługując się metodą analogiczną do metody dowodu Hermite`a, Lindemann udowodnił w 1882, że liczba pi również jest liczbą przestępną. Znane są w matematyce terminy "liczby Hermite`a", "formy Hermite`a". Do jego prac należy też szczególne rozwiązanie w liczbach całkowitych układu równań liniowych z całkowitymi współczynnikami. Problem ten został uogólniony przez innych matematyków. Hermite był przekonany ,ze liczby i funkcje analityczne nie są dowolnymi wytworami ludzkiego rozumu ,lecz ,że one istnieją poza nami, podobnie jak przedmioty realnego świata, i że matematyce odkrywają (poznają) je i badają, jak to czynią uczeni w innych dziedzinach,np. fizycy, chemicy czy zoologowie. Nic więc dziwnego ,że w jednym z listów do holenderskiego matematyka Stiltjesa, z którym przyjaźnił się napisał :"Odwracam się ze wstrętem od tego pożałowania godnego trzęsawiska funkcji bez pochodnych". Chodzi o to ,że badania podstaw analizy spowodowały potrzebę zajmowania się pewnymi funkcjami o nieoczekiwanych
i dziwacznych, jak na owe czasy, własnościach. Poincare wyrażał się nieprzychylnie o wynajdywaniu nowych funkcji, nie posiadających praktycznego celu. Hermite, jak widać z jego wypowiedzi, był ich oczywistym przeciwnikiem. Tymczasem owe badania przyczyniły się do powstania w XIX wieku nowej dziedziny matematyki, występującej obecnie pod nazwą teorii funkcji rzeczywistych. W obszernej korespondencji ze Stiltjesem powstało czterotomowe dzieło pt ."Correspondance" (wydane w 1905 roku ,zawierające szereg prac z zakresu funkcji zmiennej zespolonej.)Hermiote`a cechowała duża skromność, której przykładem jest fakt ,że w liście do Stiltjesa, dotyczącym zagadnień matematycznych, przyznawał on rację Stiltjesowi, której sobie odmawiał. Zmarł w Paryżu 14 stycznia 1901 roku. Powrót
SOFIA KOWALEWSKA(1850-1891) : Wśród około setki najwybitniejszych matematyków kilku ostatnich wieków znalazła się również kobieta. Jest nią Rosjanka - Zofia Kowalewska (z domu Korwin-Krukowska). W carskiej Rosji kobiety nie miały możności zdobycia wyższego wykształcenia, gdyż wstęp na uczelnie był dla nich zamknięty. Dlatego też Kowalewska napotykała poważne trudności w zdobywaniu wiedzy. Jako kobieta nie może się dostać na Uniwersytet w Moskwie. Bierze więc prywatne lekcje wyższej matematyki,w której to dziedzinie wykazywała duże zdolności już od wczesnych lat. Następnie wyjeżdża do Niemiec i dopiero tam na Uniwersytecie w Heidelbergu słucha wykładów matematyki i fizyki. Później przenosi się do Berlina, gdzie zwraca na siebie uwagę wybitnego matematyka Weierstrassa. On to zachwycony jej zdolnościami udziela jej prywatnych lekcji. Wspólnie omawiają nowości naukowe, dotyczące m.in. geometrii nieeuklidesowej. Weierestrass mówił później,że miał bardzo niewielu uczniów
,którzy pod względem zdolności, pilności i umiłowania nauki dorównywali Kowalewskiej. W tym czasie Kowalewska pisze trzy prace, z których każda - zdaniem Weierstarssa - była wystarczająca dla otrzymania doktoratu. Do prac tych należą :"Przyczynek do teorii równań różniczkowych o pochodnych cząstkowych", "Przyczynki i uwagi o badaniach Laplace`a nad postaciami pierścienia Saturna" oraz "O sprowadzeniu niektórych całek Abela do całek eliptycznych". Za prace te otrzymuje tytuł doktora filozofii z odznaczeniem. Wyniki pierwszej pracy uwzględnione są obecnie w obszerniejszych podręcznikach analizy matematycznej pod nazwą twierdzenia Cauchy - Kowalewskiej. Podała ona prostszy dowód pierwotnego twierdzenia Cauchy`ego i nadała twierdzeniu formę ostateczną oraz - co najważniejsze - uogólniła wynik na układ równań różniczkowych cząstkowych. Po powrocie do Rosji utrzymuje żywy kontakt z elitą naukową tego kraju, mianowicie Czebyszewem, Mendelejewem,Stoletowem a także fińskim matematykiem Mittag-Lefflerem, dzięki które
otrzymuje w roku 1883 katedrę matematyki na Uniwersytecie w Sztokholmie. Jest bardzo szczęśliwa z tego powodu, gdyż jak sama mówi ,"funkcje profesora zawierają w sobie coś szlachetnego. Nie mówiąc już o ogromnym znaczeniu, jakie ma dla mnie pełnienie obowiązków docenta,byłabym szczęśliwsza, gdybym mogła utorować nową karierę kobietom...". Powierzenie kobiecie katedry matematyki wywołało oburzenie wśród niektórych, zaskorupiałych w przesądach ,kół uniwersyteckich. Odmawiano jej jakichkolwiek zasług naukowych , oczerniano w sposób nieludzki. Jednakże nie brakło jej przyjaciół. Pewna demokratyczna gazeta pisała :"Dzisiaj mamy zaszczyt głosić o przyjeździe nie jakiegoś tam pospolitego księcia krwi. To księżniczka nauki, pani Kowalewska, zaszczyciła swymi odwiedzinami nasze miasto i będzie pierwszym docentem - kobietą w całej Szwecji". Po roku Kowalewska otrzymuje nominację na profesora. W 1888 r. pisze swą podstawową pracę naukową "O zagadnieniu obrotu ciała sztywnego wokół nieruchomego punktu". Praca ta
dostaje pierwszą nagrodę na konkursie dotyczącym tego zagadnienia, ogłoszonym przez Paryską Akademię Nauk. Niedługo potem czekała Kowalewską nagroda za dorobek naukowy od Szwedzkiej Akademii Nauk. Współpracuje z wielkimi matematykami francuskimi jak Poincare, Hermite .Staje się znakomitością, znaną i cenioną przez wszystkie ówczesne koła naukowe. Należy chyba wspomnieć też o jej doskonałych zdolnościach językowych (władała pięcioma językami) oraz literackich (pisze artykuły popularnonaukowe do gazet, recenzje teatralne, opowiadania, kilka powieści o charakterze autobiograficznym, m.in. powieść "Nihilistka", której druku zabroniła ówczesna cenzura; wydrukowano ją dopiero w 1928 roku.). Umiera w Sztokholmie wskutek przeziębienia i choroby płuc. Umiera w pełnym rozkwicie swych zdolności i sławy. Powrót
MARIUS SOPHUS LIE(1842-1899) : Matematyk norweski urodził się w 1842 roku w Nordfjordeit koło Bergen. Kształcił się najpierw na Uniwersytecie w Christianii, później w 1869 r wyjechał do Berlina, gdzie zaprzyjaźnił się z Kleinem (który był wówczas asystentem Pluckera w Bonn). W 1871 r. Lie objął stanowisko asystenta na Uniwersytecie w Christianii. W tym samym okresie ogłosił pracę doktorską i został mianowany profesorem w tym mieście. W rou 866 obejmuje po Kleinie katedrę w Lipsku, gdzie wykłada do 1898 roku. W roku 1898 wraca do Christianii. Jednakże zdrowie nie pozwala mu już długo pracować i w roku 1899 kończy życie. Lie poświęcił się systematycznym badaniom ciągłych grup przekształceń i ich niezmienników. Pokazał ich wielkie znaczenie w wielu działach matematyki oraz mechaniki. Przy ich pomocy usystematyzował zasady geometrii, mechaniki, równań różniczkowych, zwyczajnych i cząstkowych. Odkrył on także transformacje stycznościowe, a wraz z nimi klucz do
całej mechaniki Hamiltona,jako część teorii grup. Lie nie tylko tworzył samodzielnie, ale również współpracował z wieloma wybitnymi matematykami : z Kleinem,Riemannem, Poincare i Helmholtzem. Wspólne wyniki Lie i Helmholtza doprowadziły ich do tzw. "problemu przestrzeni Lie-Helmholtza", który posiadał znaczenie nie tylko dla teorii grup i teorii względności, lecz także dla fizjologii. Wyniki prac Lie zebrane zostały w większej części już po śmierci uczonego przez jego uczniów i wydane drukiem. Prace Lie zostały też wzbogacone i uzupełnione przez francuskiego matematyka Cartana. Powrót
HERMANN MINKOWSKI(1864-1906) : Gdy przegląda się historię matematyki czasów nowożytnych, to rzadko się zdarzają okresy, w których przedstawiciele matematyki niemieckiej nie mieli by czegoś do powiedzenia. I chociaż zdarzały się ,jak w każdej dziedzinie ludzkiej działalności, okresy zahamowań, a nawet chwilowego upadku, to przecież wkład matematyki niemieckiej do ogólnego jej dorobku daje się chyba porównać tylko z jej francuskim odpowiednikiem. Hermann Minkowski zapewne nie uchodzi za najbardziej reprezentatywnego przedstawiciela szkoły niemieckiej przełomu XIX i XX wieku. W każdym razie jego dorobek naukowy jest niemały, a niektóre jego osiągnięcia, np. geometryczna teoria liczb, inspirowały innych matematyków (np. Hilberta). Minkowski urodził się w 1864r, w miasteczku Aleksoty w guberni miśnieńskiej. Będąc jeszcze dzieckiem, znalazł się z całą rodziną w Niemczech, gdzie ukończył gimnazjum i uniwersytet. W 1881 roku 17 letni młodzieniec bierze udział w konkursie
na teorię przedstawienia liczby naturalnej jako sumy kwadratów pięciu innych liczb naturalnych, ogłoszonym przez Akademię Paryską, za którą to pracę otrzymuje nagrodę. Serię następnych prac poświęca Minkowski geometryzacji teorii liczb, czym dał początek dziedzinie matematycznej o tej nazwie. Wprawdzie Dirichlet i Hermit także posługiwali się geometrią w teorii liczb, ale dopiero Minkowski podjął się jej systematycznego wprowadzenia we wszystkie działy tej teorii, podając tą metodą ogólne twierdzenie z zakresu analizy wielkości nieciągłych. Warto dodać ,że poza wieloma nowymi ,często bardzo głębokimi w samej teorii liczb wynikami, geometria liczb, sama w sobie, wyróżniała się specyficznym urokiem i elegancją. Nie jest wykluczone, że metoda owa nasunęła Hilbertowi pomysł geometryzacji analizy, który dał taka ważne idee, jak przestrzeń Hilberta i inne. Druga seria prac Minkowskiego dotyczyła geometrii i objęła tematyką geometrię ciał wypukłych. Przy końcu swego stosunkowo krótkiego życia (zmarł mając 42 lata)
Minkowski zajął się geometryzacją jeszcze jednej teorii, tym razem fizycznej teorii względności. Zyskała mu ona szeroki rozgłos i w związku z nią najczęściej się go wymienia. Czterowymiarowa przestrzeń występująca w tej teorii nosi nazwę przestrzeni Minkowskiego-Poincare. Powrót
RICHARD DEDEKIND(1831-1916) : Wybitny matematyk niemiecki Ryszard Dedekind urodził się w Brunszwiku. Wykształcenie otrzymał na słynnym Uniwersytecie w Getyndze u takich sław matematycznych jak Gauss i Dirichlet. Już w wieku 23 lat habilitował się, uzykując tytuł docenta w Getyndze, a w 1858 został profesorem Instytutu Politechnicznego w Zurychu. Od roku 1862 do roku 1864 wykładał w Wyższej Szkole Technicznej w Brunszwiku. Był członkiem Berlińskiej, Paryskiej i Rzymskiej Akademii Nauk. Głównym zagadnieniem jakim interesował się Dedekind, była teoria liczb. Zasadnicze wyniki, które osiągnął w tej dziedzinie, zebrał w specjalnym, 11 tomie uzupełnień do prac Dirichleta. jest on pierwszym, który w sposób ścisły i najbardziej nowoczesny podał teorię liczb rzeczywistych opartą na podstawowym pojęciu tzw. przekroju liczb rzeczywistych. Podał on szereg ogólnych pomysłów, wprowadził wiele takich zupełnie nowych pojęć jak pierścień, grupa i struktura, co stworzyło klucz
do nowoczesnej algebry (m.in. ugruntował tzw. algebraiczną teorię liczb).Pojęcia, które wprowadził już na stałe do algebry współczesnej , dały mocne podstawy do badania w wielu działach matematyki. Oprócz teorii liczb ,zajmował się także arytmetyką i teorią mnogości. Dedekind był jednym z pierwszych matematyków, którzy ugruntowali matematykę na podstawach logicznych i uczynili z niej naukę dedukcyjną. Badania Dedekinda umożliwiły połączenie różnych działów matematyki w jeden system, dlatego też były bardzo ogólne. Choć Dedekind umarł dawno, wyniki jego przetrwały bez żadnych zmian i poprawek, ponieważ były na wskroś nowoczesne. Przekrój Dedekinda i pewnik Dedekinda są dobrze znane każdemu studiującemu matematykę. Dlatego też Dedekind jest uważany za współtwórcę nowoczesnych badań matematycznych. Powrót
GEORG CANTOR(1845-1918) : Wybitny niemiecki matematyk Georg Cantor urodził sięw Petersburgu w 1845 roku. Dzieciństwo spędził w Rosji, gdzie jego ojciec był urzędnikiem palcówki dyplomatycznej. Do gimnazjum uczęszczał już w Berlinie. Studiował następnie matematykę kolejno w Zurychu, Getyndze i w Berlinie, gdzie w roku 1867 uzyskał na Uniwersytecie tytuł magistra. Z kolei przeniósł się do Halle, gdzie objął stanowisko asystenta na Uniwersytecie. W roku 1869 Cantor habilitował się, a w trzy lata później został profesorem nadzwyczajnym. W roku 1879 mianowano go profesorem zwyczajnym i do roku 1913 był kierownikiem Katedry Matematyki na Uniwersytecie w Halle. Pierwsze jego prace dotyczyły szeregów Fouriera i teorii liczb niewymiernych. W latach 1874-1985 opublikował prace, w których sformułował podstawy stworzonej przez siebie teorii mnogości (teorii zbiorów). Jest to dział matematyki traktujący o własnościach zbiorów w oderwaniu od cech elementów zbioru.
Kilkanaście kolejnych lat swojej twórczości naukowej poświęcił Cantor dalszemu rozwinięciu teorii mnogości. Wykazał istnienie nieekwiwalentnych (tzn. mających różne moce) nieskończonych mnogości, sformułował ściśle pojęcie mocy mnogości i przeprowadził dowód ,że zbiór liczb rzeczywistych jest "liczniejszy" (ma większą moc) niż zbiór liczb wymiernych. Cantor dał podstawy teorii mnogości punktowych, zajmującej się zbiorami leżącymi w przestrzeni zwykłej lub abstrakcyjnej. Opublikował tak wiele znakomitych i interesujących prac w teorii mnogości, że nie sposób podać nawet ich części. Wydana nakładem Niemieckiej Akademii "Teoria Mnogości" (zbiór prac Cantora) jest obszernym trójtomowym dziełem. Od roku 1897 ustaje tak niezwykle płodna twórczość Cantora. Ciężka choroba i ciągłe ataki nie pozwalają na twórczą pracę umysłową. Od tego czasu ogłosił jedynie kilka publikacji dotyczących podstaw matematyki i logiki matematycznej. Idee Cantora u współczesnych mu uczonych spotkały się początkowo z niezrozumieniem i
ostrą krytyką. Dopiero w kilkanaście lat po ich ogłoszeniu zyskały sobie uznanie wśród uczonych i wywarły olbrzymi wpływ na dalszy rozwój matematyki. Powrót
HENRI JULES POINCARE(1854-1912) : Wybitny francuski matematyk, fizyk, astronom-teoretyk, urodził się w Nancy, 24 kwietnia 1854 roku. W 1873 wstąpił do Szkoły Politechnicznej w Paryżu, a w roku 1879 zostaje inżynierem górniczym i doktorem nauk matematycznych. W latach 1879 - 1881 był lektorem na wydziale nauk ścisłych w Uniwersytecie w Caen. W roku 1881 został lektorem, a od 1886 aż do śmierci był profesorem Sorbony w Paryżu. Należy do największych matematyków francuskich drugiej połowy dziewiętnastego wieku. Jego wykładu co roku obejmowały inne zagadnienia i były wydawane przez słuchaczy. Wykładał fizykę mechaniczną i eksperymentalną (doświadczalną), fizykę matematyczną, rachunek prawdopodobieństwa, mechanikę nieba. Charakterystyczną cechą prac naukowych Poincarego w dziedzinie matematyki był nie tylko kierunek klasyczny, równocześnie bowiem wskazał on drogę rozwoju dla nowoczesnej matematyki .Wiele czasu poświecił teorii równań różniczkowych z algebraicznym
współczynnikami; te prace spowodowały ,że zajął się zagadnieniem nowej klasy funkcji przestępnych (transcendentnych), tzw. funkcjami automorficznymi. W pray tej korzystał między innymi z geometrii Łobaczewskiego. Zajmował się również topologią i podstawami matematyki. Ten naukowiec-teoretyk, który wydał znakomite dzieła :"Wolność nauki" (1905), "Nauka i hipoteza" (1906) umiał z wielkim mistrzostwem wykorzystać osiągnięcia czystej matematyki dla potrzeb matematyki stosowanej. Prace Poincarego w dziedzinie fizyki matematycznej dotyczyły równowagi obracającego się ciała płynnego (1885). W roku 1889 Poincare otrzymał nagrodę króla szwedzkiego Oskara za "zadanie trzech ciał". W latach 1892-1893 ogłosił trzytomową pracę "Methodes nouvelles demacanique celeste" (Nowe metody mechaniki nieba), w której podzielił idee Laplace`a. Również jak Laplace, Poincare pracuje nad zagadnieniami rachunku prawdopodobieństwa. O zasługach Poincarego dla nauki niech świadczy fakt ,że w roku 1887 został członkiem Akademii Nauk w Paryżu
,ponadto był członkiem 22 akademii nauk oraz doktorem honorowym 8 uniwersytetów. Poincare był również filozofem, zwolennikiem machizmu;ulegał wpływom pragmatyzmu i neokantzymu. Nie przyznawał on obiektywnego istnienia materii i w swych pracach pochwalał poglądy agnostyków. Twierdził, że wartość naukowej teorii znajduje się nie w prawidłowości i odtwarzaniu rzeczywistości, lecz korzyści i celowości jej zastosowania. Poincare umarł w Paryżu 17 lipca 1912 roku. Powrót
CAMILLE JORDAN(1838-1922) : Miara Jordana, krzywa Jordana - oto niektóre z pojęć spotykanych w kursie analizy matematycznej. nazwisko Jordana występuje także w innych gałęziach matematyki, np. w teorii funkcji, algebrze, a przede wszystkim w teorii grup. Miejscem jego urodzenia była miejscowość Croix-Rousse blisko Lyonu, lecz prawie całe jego życie związane było z paryską uczelnią techniczną - l`Ecole Polytechique, gdzie Jordan studiował, a potem przez czterdzieści lat wykładał. Było to tuż po okresie narodzin nowej, mającej ogromne znaczenie ideii - podanej przez nieszczęsnego geniusza Ewarysta Galois - teorii grup. W umyśle Jordana znalazła ona głębokie i pełne zrozumienie i obok Kleina i Lie stał się Jordan aktywnym jej propagatorem, rozwijając i systematyzując metody z nią związane. Taki właśnie charakter miało głębokie i świetnie napisane dzieło "Traite des substitutions et des equations algebriques" (1870) będące rozwinięciem metod Galois w teorii równań
algebraicznych. Zarówno ta, jak i wszelkie inne prace, które wymienimy, posiadały właściwe Jordanowi cechy : wrogość dla werbalizmu i rozwlekłości. Tak na przykład drugie jego najlepsze dzieło, trzytomowy wykład analizy matematycznej - "Course d`analyse" (1883-1887) może uchodzić za model zwięzłości , połączonej z wielką precyzją i wewnętrzną dyscypliną. Te wszakże cenione cechy sprawiały wiele kłopotów jego czytelnikom jego prac i słuchaczom jego wykładów. Toteż zdaniem matematyków, ogromowi wartości w nich zawartych dorównywała trudność w ich percepcji. Szereg prac Jordana, nie wydanych książkowo, publikowały francuskie i włoskie periodyki matematyczne. Dotyczyły one grup ruchu wielościanów, równań różniczkowych liniowych, geometrii wielowymiarowej, arytmetycznej teorii forma kwadratowych i teorii grup. Wspomniany wyżej szczególny ascetyzm w matematyce występował także w życiu prywatnym Jordana. Chociaż był właścicielem hotelu na przedmieściu Paryża, zajmował w nim tylko jeden gabinet. Tutaj zgromadził
tylko najbardziej niezbędne do pracy przedmioty: skromne i nieliczne meble, książki i .... czarną tablicę. Jordana cechowała niechęć do wszelkich wizyt,w czym posuwał się tak daleko ,żę gości traktował jak intruzów. Camille Jordan zmarł w Mediolanie w 1922 roku. Zdaniem Sylvestra, wybitnego matematyka angielskiego, Jordan zajmował się najtrudniejszymi, wymagającymi maksimum wysiłku i poświęcenia zagadnieniami matematycznymi. Dla wielu współczesnych Jordanowi matematyków pozostawał zawsze wybitną postacią francuskiej szkoły matematycznej. Powrót
ALEKSANDR MICHAJŁOWICZ LAPUNOW(1857-1918) : Twórczość Aleksandra Michajłowicza Lapunowa przypada na okres rozwoju matematyki, kiedy większość jej problemów nie miała w niej samej swego źródła, lecz stykano się z nimi w pracy nad rozwiązywaniem różnych zagadnień technicznych i fizycznych. Do tego rodzaju należała też twórczość Lapunowa. Lapunow przyszedł na świat w 1857 roku w Jarosławiu. Po śmierci swojego ojca, znanego astronoma, Aleksander rozpoczyna w 1870 r. naukę w niżnogrodzkim gimnazjum, którą kończy ze złotym medalem w roku 1876. W tym samym roku wstępuje na Uniwersytet Petersburski, na wydział przyrodniczy, który po miesiącu zmienia na matematyczny. Słucha tutaj wykładów słynnego Czebyszewa, a także bierze udział w konkursie wewnątrz wydziałowym, uzyskując za swą pracę złoty medal. Po ukończeniu studiów w 1880 i uzyskaniu stopnia kandydata młodego naukowca zatrudnia katedra mechaniki. Z nią też przede wszystkim związane będą prace Lapunowa, które
w swoim aspekcie matematycznym dotyczyć będą teorii układów równań różniczkowych zwyczajnych, zagadnienia Dirichleta i teorii potencjału. Ponadto Lapunow sięgnie do rachunku prawdopodobieństwa, dowodząc tu nazwanego jego nazwiskiem twierdzenia Lapunowa, które weszło trwale do tej dziedziny jako jedno z najważniejszych twierdzeń granicznych. Wpływ na działalność naukową Lapunowa wywarł jego nauczyciel i wychowawca Czebyszew. Zagadnienie Czebyszewa, jakie przedstawił początkującemu jeszcze naukowcowi jego autor,nurtowało Lapunowa przez całe życie. Poświęcił mu też Lapunow wiele swych prac mających niemałe znaczenie, by je w końcu w pełni rozwiązać u schyłku swego życia. Wczesna próba znalezienia żądanego rozwiązania staje się jego pracą magisterską, którą obronił w 1885 roku. Jesienią tegoż roku Lapunow został docentem na katedrze matematyki stosowanej Uniwersytetu Charkowskiego. Stawiając wysokie wymagania dla swej twórczości, Lapunowa wzdragał się przed ubieganiem się o tytuł doktora, chociaż wiele
z jego prac które publikował, aż nadto do tego wystarczały. Uczynił to dopiero po skrupulatnym przygotowaniu znakomitej pracy "ogólne zadanie o trwałości ruchu" wydanej przez Rosyjską Akademię Nauk w 1892 roku. Autor rozwiązał w niej wiele zagadnień dotyczących równań różniczkowych zwyczajnych. Lata rewolucji rosyjskiej 1917 roku rzucają Lapunowa do Odessy. Oderwany od swej pracy, załamany śmiercią swej żony, w końcu 1918 roku Lapunow popełnia samobójstwo. Zasługi Lapunowa, jego wkład do matematyki były niezwykle cenne. Toteż wiele uczelni krajowych i zagranicznych, wiele akademii, w tym także Francuska Akademia Nauk , nadały mu godność członka - korespondenta. Powrót
ANDRIEJ ANDRIEJEWICZ MARKOW(1856-1922) : Z rosyjskiego alfabetu (36 znaków) wyjęto na chybił trafił 6 liter i ustawiono je w takim porządku, w jakim były wyjęte. Dwaj świadkowie potwierdzają ,że litery te ułożyły się w wyraz MOSKWA. Pytamy się, jakie jest prawdopodobieństwo ,że zeznania świadków są prawdziwe, jeżeli ich skłonność do mówienia prawy wyraża się ułamkiem 9/10... Obliczono ,że prawdopodobieństwo takie jest mniejsze niż 1/300...Przykład ten wskazuje, jak mała jest możliwość takiego zdarzenia, a przecież nie uwzględniono jeszcze wszystkich dowolności, przy 50 000 słów sześcioliterowych w języku rosyjskim istniej jeszcze duża możliwość pomyłki świadków... Jest to jedno z wielu zagadnień z dziedziny rachunku prawdopodobieństwa. Zadanie to prawidłowo rozwiązał A.A.Markow w swej pracy "Obliczanie prawdopodobieństwa". ten wybitny rosyjski matematyk zajmował się głównie rachunkiem prawdopodobieństwa. Jego prace z tej dziedziny walnie przyczyniły się do
dalszego jej rozwoju. Dzięki jego pracom można dzisiaj rozwiązywać wiele zagadnień statystycznych z zakresu fizyki, chemii, matematyki itp. Andrzej Markow urodził się w 1856 roku w guberni riazańskiej. Ojciec jego był urzędnikiem niskiego stopnia. Matematyka zaczęła młodego Markowa interesować już w gimnazjum, po którego ukończeniu wstąpił na Uniwersytet Petersburski na wydział matematyczny. Ukończył studia w 1878 roku z tytułem kandydata nauk. W tym samym roku uzyskał złoty medal za pracę z zakresy równań różniczkowych, po czym przyjął pracę na Uniwersytecie Petersburskim, robiąc błyskawiczną karierę naukową. W roku 1880 zostaje docentem,a w sześć lat później profesorem, a w roku 1905 nadano mu tytuł zasłużonego profesora. Równocześnie pracował w Akademii i w 1896 roku otrzymał tytuł członka Akademii. Wszystkie prace Markowa są związane ze szkołą Czebyszewa. Zajmował się kolejno teorią liczb, analizą matematyczną i rachunkiem prawdopodobieństwa. Wiele dowodów Markowa znanych jest obecnie na całym świecie
jako dowody podstawowe, szczególnie zaś znane są zależności nazwane jego imieniem. Najważniejsze z nich - wielomiany Markowa i łańcuchy Markowa. Zależności te oddają nieocenione usługi w obliczaniu wyników doświadczalnych z innych dziedzin nauki, stały się też podstawą do wielu nowych prac teoretycznych z zakresu analizy matematycznej i rachunku prawdopodobieństwa. Markow znany jest nie tylko jako wielki matematyk, ale i jako człowiek solidaryzujący się w śmiały sposób z ideami postępu. I tak np. gdy Lew Tołstoj za swoją działalność został oficjalnie wyłączony z kościoła rosyjskiego, Markow w liście do władz kościelnych odmawia swej przynależności do cerkwi. Gdy Gorkiemu nie przyznano tytułu członka Akademii Nauk, Markow zrzeka się wszystkich tytułów i odznaczeń nadanych mu przez Akademię. Markow całe życie poświęcił nauce. Ostatnią pracę ogłosił na parę miesięcy przed śmiercią, zmarł20 lipca 1922 roku. Powrót
ERIK IVAR FREDHOLM(1866-1927) : Szwedzki matematyk Erik Ivar Fredholm urodził się w roku 1866. W 1885 zaczął studiować na Politechnice w Sztokholmie, gdzie przebywał tylko rok. W następnym roku studiuje na Uniwersytecie w Upsali, a w roku 1888 przenosi się do Sztokholmu, gdzie kontynuuje naukę do 1893 roku. W roku 1898 uzyskuje doktorat i wkrótce zostaje docentem,a w roku 1906 profesorem Uniwersytetu w Sztokholmie. Fredholm początkowo zajmował się równaniami różniczkowymi i uzyskał szereg ważnych wyników. Jednakże później zaczął interesować się równaniami całkowymi, tzn. równaniami zawierającymi funkcję niewiadomą pod znakiem całki. Fredholm był pierwszym, który zaczął badać te równania i opracował ogólne metody rozwiązywania pewnych typów równań całkowych. Otrzymały one nazwę równań Fredholma. Z wyników jakie uzyskał, słynny jest wyznacznik Fredholam oraz trzy twierdzenia. Udowodnił je w teorii równań całkowych. Znaczenie wyników Fredholma jest szczególnie
ważne dla rozwoju szeregu zagadnień fizycznych. Polega ono na tym ,że większość równań różniczkowych wraz z ich warunkami brzegowymi można zamienić na równoważne pojedyncze równania całkowe. Jeśli te równania całkowe można rozwiązać, to trudności matematyczne nie powiększają się zbytnio nawet przy wzroście ilości zmiennych niezależnych, podczas gdy równania różniczkowe są znacznie bardziej skomplikowane w trzech wymiarach niż dwóch. Jakkolwiek więc prace Fredholma ograniczają się w zasadzie do równań całkowych, to jednak widzimy ,że pionierskie badania pchnęły całą wiedzę o równaniach różniczkowych naprzód i wniosły potężny wkład do ich ujednolicenia. Widzimy także bezpośrednio zastosowanie zagadnień przez niego rozważanych do potrzeb najnowocześniejszej techniki, o czym świadczą różne książki z takich dziedzin jak fizyka i chemia. Powrót
ZYGMUNT JANISZEWSKI(1888-1920) : Zygmunt Janiszewski urodził się 12 lipca 1888 roku w Warszawie. Gimnazjum ukończył we Lwowie w 1907 roku. Studia z dziedziny matematyki i filozofii odbył za granicą. Doktoryzował się w 1911 roku u Lebesgue`a,habilitował w 1913 r. na Uniwersytecie Jana Kazimierza we Lwowie, w którym wykładał do wybuchu I wojny światowej. Okres jej trwania spędza częściowo w wojsku, następnie w okolicach Radomia, gdzie musiał się schronić na skutek odmowy przysięgi rządowi austriackiemu. W roku 1918 zostaje powołany na profesora przez Uniwersytet Warszawski. Umarł 3 stycznia 1920 roku w pełni sił twórczych. Janiszewski odznaczał się ogromną siłą charakteru i odwagą myśli. Życie, naukę i obowiązki traktował poważnie. Pracy powierzchownej nie uznawał. Tak bardzo krótkie życie uczonego wypełnione było pracą naukową, dydaktyczną i organizatorską. Jest autorem twierdzeń z topologii znanych jako twierdzenia Januszewskiego;stanowią one trwałą i
powszechnie uznaną zdobycz matematyki. Oprócz topologii gdzie posiadał własne odkrycia, znał gruntownie logikę matematyczną. Stosował ją z powodzeniem do wykrywania braków i niejasności w strukturze pojęć matematycznych. Ale nie tylko - przydatna była mu także przy przygotowaniu wykładów .Do działalności dydaktycznej tego młodego profesora należy zaliczyć szereg prac publikowanych w "Poradniku dla samouków." Rzut oka na I tom "Poradnika" wskazuje ,że Janiszewski był również filozofem. Działalność organizatorska Janiszewskiego wiąże się ściśle z sytuacją, w jakiej znajdowała się Polska i jej nauka. Były to pierwsze chwile niepodległości po długiej niewoli. Naukę polską w większości reprezentowały jednostki przebywające poza granicami kraju. Przyznać należy również ,że rozwój matematyki polskiej pozostawał w tyle za rozwojem matematyki na Zachodzie. Janiszewski na łamach "Nauki Polskiej" - rocznika Kasy im. Dra Józefa Mianowskiego - wypowiada się zdecydowanie za stworzeniem atmosfery twórczej pracy, klimatu
naukowego, stworzenia własnego czasopisma naukowego, poświęconego "wyłącznie jednej z tych gałęzi matematyki, w których mamy pracowników wybitnych,prawdziwie twórczych i licznych. Pismo takie stałoby się nieodzownym dla każdego pracującego w danej gałęzi matematyki, znalazłoby czytelników wszędzie, a w krótkim czasie pozyskałoby poważnych współpracowników za granicą. Zajęlibyśmy przez to należne nam stanowisko w nauce europejskiej, gdyż nie tylko wiele naszych prac, rozproszonych po pismach polskich, pokazałoby się w ten sposób światu, lecz bylibyśmy znani już nie jako jednostki, lecz zwarta grupa Polaków. Samo istnienie i rozpowszechnianie takiego pisma, wydawanego w Warszawie, świadczyłoby o naszym życiu naukowym". Takie pismo - Fundamenta Mathematicae - powstało (nie jest oczywiście zasługą jedynie Janiszewskiego). Pierwszy jego tom ukazał się z nekrologiem Janiszewskiego. Przyczyniło się ono w dużym stopniu do stworzenia samodzielnego stanowiska matematyki polskiej. A oto kilka momentów z życia profesora
Janiszewskiego, które doskonale obrazują jego postawę moralną. Będąc jeszcze w szkole, rozdziela swą odzież wśród kolegów. W 1916 roku, służąc w wojsku, odmawia przyjęcia naszywki , jak również odmawia przysięgi na wierność rządowi austriackiemu .Schroniwszy się w Radomiu, organizuje za własne oszczędności ochronkę dla bezdomnych dzieci i samodzielnie ją prowadzi do końca wojny. By "i po śmierci być przydatnym", własne ciało przeznacza dla prosektorium. Powrót
CHARLES PEARSON(1857-1936) : Karol Pearson znany matematyk - statystyk, biolog i filozof - idealista urodził się 27 marca 1857 roku w Londynie jako syn wybitnego adwokata i radcy królewskiego - Williama Pearsona. Pearson kształcił się początkowo w Londyńskim Kolegium Uniwersyteckim, a w roku 1875 został przyjęty do jednego z kolegiów w Cambridge, gdzie w 1879 uzyskuje tytuł magisterski. Początkowo Pearson zamierzał iść w ślady ojca i zostać prawnikiem. Szybko jednak rezygnuje z tego zamiaru i rzuca się w wir życia studenckiego. Wkrótce jednak wyjeżdża do Niemiec, początkowo studiuje w Heidelbergu fizykę, następnie uczęszcza w Berlinie na wykłady prawa rzymskiego oraz z zakresu teorii Darwina. Ciekawe jest że Pearson z wielką zachłannością starał się poznać kulturę i obyczajowość Niemców. Przebywał wiele z prostymi ludźmi, z którymi dyskutował równie łatwo jak z wybitnymi uczonymi. Ze znanych ludzi,pod których wpływem powstały jego późniejsze poglądy i
zainteresowania, warto wymienić Johna Routh. Było to przypuszczalnie największy matematyk jaki pracował w Cambridge. Spośród jego 700 uczniów, około 500 stało się pracownikami naukowymi. Prawie całe życie trwało powiązanie K.Pearsona z Uniwersytetem Londyńskim. W wieku 27 lat (po powrocie z Niemiec)mianowany zostaje tam profesorem Zastosowań Matematyki i Mechaniki. Odtąd aż do samej śmierci, która nastąpiła nagle 27 kwietnia 1936 roku, życie jego wypełnia praca w murach tej uczelni. Uczony, krótkie wakacje letnie spędzał w domku wiejskim, gdzie pracował tak samo intensywnie. I w czasie właśnie takich wakacji napisał swe monumentalne dzieło "Życie Franciszka Galtona". Największe jego zasługi z dziedziny statystyki matematycznej to:
1. rozwój teorii korelacji i jej zastosowań do problemów dziedziczności i ewolucji;
2. wprowadzenie testu chi - kwadrat, stosowanego między innymi do zbadania zgodności pomiędzy wynikami otrzymanymi z doświadczenia a przewidywanymi wynikami teoretycznymi;test ten mający szerokie zastosowanie należy do najważniejszych testów statystyki matematycznej;
3. wprowadzenie systemu krzywych częstości (zwanego systemem krzywych częstości Pearsona)jako narzędzia do matematycznego opisania zjawisk przyrodniczych;
4. użycie po raz pierwszy metody momentów;
5. wydanie tablic dla statystyków i biometryków wraz ze szczegółowymi objaśnieniami dotyczącymi ich stosowania
Pearson był wielkim autorytetem również w dziedzinie eugeniki. Był profesorem eugeniki Uniwersytetu Londyńskiego oraz dyrektorem Międzynarodowego Laboratorium Eugeniki F.Galtona. Za jego liczne prace z matematycznej teorii ewolucji i dziedziczności został nagrodzony Medalem Darwina Towarzystwa Królewskiego Eugeniki, którego w 1896 roku został członkiem. Wielką zasługą tego uczonego było założenie w 1900 roku czasopisma "Biometrika", którego wydawaniem kierował aż do śmierci (przez 36 lat). W latach 1925-1926 był wydawcą "Roczników Eugeniki". Pearson był także wybitnym pedagogiem. Miał rzadki dar jasnego przekazywania innym swej wiedzy. Powrót
SAMUEL DICKSTEIN(1851-1939) :W latach walki z uciskiem politycznym i rusyfikacją szkolnictwa polskiego po upadku powstania styczniowego jednym z najwybitniejszych działaczy - patriotów był Samuel Dickstein. Wybitny ten matematyk, historyk nauki i działacz społeczny całe swe życie poświęcił walce o naukę polską. Samuel Dickstein urodził się 12 maja 1851 roku w Warszawie. Po ukończeniu gimnazjum studiował w Szkole Głównej. Od roku 1870 poświęcił się działalności pedagogicznej. Był początkowo nauczycielem gimnazjalnym następnie przez 10 lat prowadził własne liceum matematyczno-przyrodnicze. W 1906 roku był jednym z założycieli Kursów Naukowych (stanowiły one zaczątek przyszłego Uniwersytetu Warszawskiego), pierwszym prezesem ich Rady Naukowej i profesorem oraz założycielem Warszawskiego Towarzystwa Naukowego. Po uzyskaniu niepodległości w 1918 roku i powstaniu Uniwersytetu Warszawskiego już do końca życia pracował w tej uczelni. w roku 1919 nadano mu tytuł doktora
honoris causa Uniwersytetu Warszawskiego. Dickstein prowadził szeroką działalność wydawniczą. W 1884 r. jest jednym z założycieli "Biblioteki Matematyczno-Fizycznej". Nakładem tego wydawnictwa ukazuje się wiele świetnych podręczników akademickich. W cztery lata później zaczyna wydawać "Prace Matematyczno-Fizyczne", pierwsze w Polsce czasopismo naukowe z tej dziedziny o charakterze międzynarodowym. Od 1897 roku wydaje założone przez siebie czasopismo "Wiadomości Matematyczne". Publikuje wiele prac własnych z zakresu wyższej algebry i teorii liczb. Wydaje podręczniki i świetne własne przekłady dzieł obcych, tworzy i wprowadza polską terminologię matematyczną Zasadniczą jednak tematyką jego prac była historia matematyki. Odkrył zapomnianych lub zupełnie nieznanych wybitnych matematyków polskich, Kochańskiego i Hoene-Wrońskiego. Starał się o ściągnięcie też do Polski matematyków polskiego pochodzenia pracujących na obczyźnie. Dzięki jego inicjatywie przyjechał do Kraju pracujący we Francji wybitny matematyk
Zaremba, który później został profesorem Uniwersytetu Jagielońskiego. Prace z zakresu historii matematyki uczyniły go sławnym w świecie naukowym. Był członkiem Polskiej Akademii Umiejętności, Towarzystw Naukowych w Liege i w Pradze, członkiem honorowym Związku Czeskich Matematyków, Międzynarodowej Komisji Nauczania Matematyki. Jako dowód uznania dla prac Dicksteina stanowi fakt powołania go na stanowisko wiceprezesa Międzynarodowej Akademii Historii Nauk Ścisłych. Dickstein był nie tylko wybitnym matematykiem. Zajmował się również innymi dziedzinami wiedzy. Założył czasopismo "Ruch Pedagogiczny", przyczynił się do powstania w Polsce sieci stacji meteorologicznych, był wieloletnim kierownikiem instytucji będącej poprzedniczką PIHM-u współzałożycielem Muzeum Tatrzańskiego i Muzeum Przemysłu i Rolnictwa. Mając 85 lat powiedział kiedyś ,że po czterogodzinnym wykładzie wyższej matematyki zaczyna odczuwać jakby lekkie zmęczenie. Zmarł podczas bombardowania Warszawy 20 września 1939 roku.
Powrót
JÓZEF MARCINKIEWICZ(1910-1940) : Józef Marcinkiewicz to jeden z najlepiej zapowiadających się matematyków polskich okresu międzywojennego. Urodził się 30 marca 1910 roku w Sokółce w województwie białostockim w rodzinie chłopskiej. W 1930 rozpoczął studia na Wydziale Matematyczno-Przyrodniczym Uniwersytetu Stefana Batorego w Wilnie. Już na drugim roku studiów zaczął współpracować z prof. A.Zygmundem, który w takich oto słowach charakteryzuje swojego ucznia :"Gdy wspominam Marcinkiewicza,widzę w mej wyobraźni wysokiego, przystojnego chłopca - żywego ,wrażliwego, serdecznego ,ambitnego z dużym poczuciem humoru. Był towarzyski nie unikał zabawy, w szczególności bardzo lubił tańce i grę w brydża. Stan jego zdrowia nie był najlepszy,miał słabe płuca i musiał dbać o siebie. Interesował się sportem (może ze względu na stan zdrowia) i był dobrym pływakiem i narciarzem. Miał również inne zainteresowania intelektualne poza matematyką: powiedział mi pewnego razu
,że wstępując na uniwersytet wahał się czy wybrać matematykę ,czy też literaturę polską". W 1933 roku otrzymał magisterium z matematyki. Następnie spędził Marcinkiewicz rok w wojsku i znów wrócił do Wilna. Pracował na stanowisku młodszego asystenta na katedrze matematyki. w 1935 otrzymał tytuł doktora za pracę będącą rozszerzeniem jego pracy magisterskiej. Rok akademicki 1935/1936 spędził we Lwowie, gdzie owocnie współpracował z Kaczmarzem i Schauderem. Wynikiem tej współpracy byłą praca o multyplikatorach szeregów Fouriera oraz prace nad ogólnymi szeregami ortogonalnymi. W roku 1936 jesienią wrócił do Wilna i pracował jako starszy asystent. W 1937 roku habilitował się Wiosną 1939 roku otrzymał stypendium i wyjechał do Paryża. Od nowego roku akademickiego 1939/1940 miał objąć katedrę matematyki na Uniwersytecie Poznańskim. Niestety wybuch wojny przekreślił jego plany. Józef Marcinkiewicz był nie tylko naukowcem - był gorącym patriotą. Na wieść o zbliżającej się wojnie i mobilizacji w Polsce powrócił do
kraju. Pio klęsce wrześniowej dostał się do niewoli, by z niej już nigdy nie wrócić. Dokładna data jego śmierci nie jest znana. Przypuszcza się ,że zakończył życie wiosną 1940 roku. Przedwczesna śmierć Marcinkiewicza był ogromnym ciosem dla matematyki polskiej. Dla uczczenia Marcinkiewica ufundowana została nagroda jego imienia, przyznawana corocznie za najlepszą pracę młodym matematykom.. Powrót
HENRI LOUIS LEBESGUE(1875-1941) : Jeden z najwybitniejszych matematyków naszych czasów, Francuz Lebesgue , urodził się w Seauvais (Oise) w 1875 roku. W miasteczku tym ukończył z odznaczeniem gimnazjum, po czym wstępuje na studia w l`Ecole Normal Superieure.Po uzyskaniu tytułu magistra na wydziale matematycznym przyjmuje posadę asystenta w Katedrze Matematyki Uniwersytetu Paryskiego. Uzyskuje tam w 1902 roku stopień doktora za pracę "Całki liniowe i powierzchniowe". Rozpoczyna teraz się w życiu Lebesgue`a okres poszukiwania odpowiadającej mu pracy, która kończy się uzyskaniem stanowiska profesora na Wydziale Nauk Ścisłych Uniwersytetu w Poitier. W 1912 wraca do Paryża i przyjmuje pracę w College de France. Tam uczony ogłasza większość swych słynnych dowodów. W 1922 roku zostaje członkiem Paryskiej Akademii Nauk,a w dwa lata później nadano mu tytuł honorowego członka Londyńskiego Towarzystwa Naukowego w Londynie. Lebesgue zajmuje się początkowo szeregami
Fouriera, ogłaszając kilka prac z tej dziedziny. Jego przełożony narzucił mu tematykę z zakresu całkowania, domagając się wielkich sukcesów w tej dziedzinie. Lebesgue w rok później ogłasza swą słynną definicję całki określonej, która znana jest obecnie jako "całka Lebesgue`a". Dzięki tej definicji całkować można nadzwyczaj szeroką klasę funkcji. Całka Lebesgue`a jest jednym z największych osiągnięć współczesnej analizy matematycznej. O wartości dzieła Lebesgue`a zdecydowała jego teoria różniczkowalności, zbudowana równolegle z teorią całki. Dzięki temu odkrycie to znalazło tyle zastosowań w różnych działach analizy, a punktu widzenia metodologicznego zbliżyło dwie podstawowe idee całki - całkę oznaczoną i funkcję pierwotną - rozdzielonych z chwilą wyjścia poza całkowanie funkcji ciągłych. Jednym z ciekawszych pomysłów Lebesgue`a jest takie rozszerzenie miary zbioru punktów, przy którym miara zbioru wszystkich liczb wymiernych jest równa 0. Wielką jego zasługą było również wykroczenie w swoich badaniach
poza funkcje ciągłe, którymi dotychczas zajmowali się matematycy. Za swe wybitne osiągnięcia zostaje w 1917 roku odznaczony orderem .Umiera w Paryżu 26 lipca 1941 roku,zostawiając niezwykle bogaty dorobek naukowy. Powrót
STANISŁAW ZAREMBA(1863-1942) :Jeśli mówi się o matematykach krakowskich, o ich wkładzie w rozwój matematyki polskiej, to przede wszystkim należy wymienić Stanisława Zarembę. Uczony ten urodził się 3 października 1863 roku w Romanówce. W roku 1886 po ukończeniu Petersburskiego Instytutu Technologicznego wyjechał na studia matematyczne do Paryża. Stopień naukowy doktora uzyskał na Uniwersytecie Paryskim w roku 1889. Praca doktorska Zaremby świadczy o wielkości jego talentu. Trzy lata przed urodzeniem się Zaremby, Akademia Nauk w Paryżu ogłosiła konkurs na pewne zagadnienie z fizyki matematycznej (ocena stanu cieplnego ośrodka nieograniczonego.) Rozprawa przedstawiona przez genialnego matematyka Riemanna nie została przyjęta, ponieważ szkicowe dowody nie miały siły przekonywującej. To samo zagadnienie (30 lat później)było treścią tezy pracy doktorskiej Zaremby, w której obok rozwiązań przedstawionych przez Riemanna podał nowe rozwiązania oraz poprawne
pełne dowody dla przypadków rozpatrywanych przez Riemanna. Ta udana pierwsza praca naukowa ułatwiła mu kontakt z ówczesnymi matematykami francuskimi i tym samym w znacznym stopniu przyczyniła się do jego własnego rozwoju naukowego. W Paryżu przebywa do roku 1900. W tymże roku, powołany przez Uniwersytet Jagielloński, wraca do kraju. Zastaje tu poziom matematyki niższy w porównaniu z poziomem matematycznym środowiska francuskiego. Jako jedną z przyczyn tego stanu upatruje Zaremba w niewystarczającym przygotowaniu do studiów przez szkołę średnią. Poprawę szkolnictwa średniego widzi m.in. w zwiększeniu kadry pedagogicznej. "Uważam - pisze Zaremba w I tomie "Poradnika dla samouków" - za zadanie mające pierwszeństwo przed każdym innym wykształcenie odpowiedniej liczby sił nauczycielskich dla szkół średnich". W powiększonym gronie młodych nauczycieli szkół średnich każe szukać przyszłych pracowników nauki:"rzesza młodych nauczycieli szkół średnich i seminariów jest ośrodkiem którego wychodzą przyszli uczeni; kto
z tej młodzieży wykaże należyte uzdolnienia, ten może w zagranicznych zakładach, bardziej zasobnych od naszych szkół wyższych, pobierać dobre wykształcenie i wyrabiać się na nauczycieli szkół wyższych". Opinia ,że pracowników naukowych matematyki należy kształcić za granicą jest ,jak widać, charakterystyczna dla wypowiedzi Zaremby, jest to zupełnie zrozumiałe, jeżeli weźmie się pod uwagę własny jego rozwój naukowy i wspomniany już poziom ówczesnej matematyki polskiej. Pracę nad poprawą matematyki polskiej rozpoczyna Zaremba od redagowania podręczników. Oto ich tytuły "Zarys pierwszych zasad teorii liczb całkowitych", "Teoria wyznaczników i równań liniowych","Arytmetyka teoretyczna", "Wstęp do analizy"(dwie części), "Zarys mechaniki teoretycznej" (dwa tomy). Podręczniki jak i wykłady Zaremby, szczególnie w początkowej fazie ich studiowania, były trudne ze względu na niezwykłą ścisłość rozważań i operowanie długimi zdaniami. Były wszakże środkiem do kształcenia ducha ścisłości na progu tworzenia się
nowoczesnej matematyki polskiej. Wątpiącym w taką ścisłość, np. w rozważaniach filozoficznych, odpowiada (i uzasadnia), że "ścisłość nie tylko nie koliduje z jasnością, lecz należy do nieodzownych jej warunków".Praca dydaktyczna nie był dla Zaremby wytchnieniem od pracy badawczej. W ponad stu publikacjach, głównie z dziedziny klasycznej analizy matematycznej, ,zawarte były wyniki nowe. Wartość ich polega nie tylko na tym ,że jako nowe pobudzały uczniów jego do dalszych poszukiwań, przyczyniając się w ten sposób do wzbogacenia zakresu wiedzy. Cała działalność (naukowa, dydaktyczna i organizatorska)Zaremby została właściwie oceniona zarówno przez współczesnych, jak i potomnych. Imię Stanisława Zaremby nosi jedna z nagród naukowych Polskiego Towarzystwa Matematycznego, co jest wyrazem uznania potomnych dla Zaremby. Uczony ten posiadał liczne odznaczenia państwowe, był doktorem honoris causa Uniwersytetu Krakowskiego. "Aktywność naukowa Zaremby - pisze Lebesgue - zaważyła na tak wielu terenach badań ,że
nazwisko jego nie może być obce nikomu, kto się interesuje matematyką.". Powrót
DAWID HILBERT(1862-1943) : Dawid Hilbert obok matematyka francuskiego Poincarego uchodził bezsprzecznie za najwybitniejszego matematyka swoich czasów. Urodził się w 1862 roku w Królewcu. W rodzinnym mieście za osiągnięcia głównie z teorii niezmienników algebraicznych otrzymuje zasłużony tytuł członka Akademii. W 1895 r. zostaje profesorem w Getyndze i tam spędza już resztę swojego życia. Charakterystycznym jego zwyczajem była wieloletnia i intensywna praca nad wybranym wąskim zagadnieniem i trzeba przyznać ,że ten niezrównany mistrz na każdym polu odnosił wielkie zwycięstwo. Po swoim pierwszym wielkim sukcesie w dziedzinie teorii niezmienników (1885-93) Hilbert poświęcił się teorii liczb algebraicznych (1893-1898). W rezultacie znów powstałą bardzo oryginalna i nowoczesna praca. Następnym zainteresowaniem Hilberta były podstawy geometrii. Okazało się bowiem ,że okłady aksjomatów zarówno Euklidesa jak i Łobaczewskiego nie są układami zupełnymi i wystarczającymi
i zawierają szereg aksjomatów zbędnych wynikających z poprzednich. Zainteresowanie Hilberta geometrią uwieńczone zostało pełnym zaksjomatyzowaniem geometrii, to jest stworzeniem zupełnie niezależnego układu aksjomatów. Osiągnięcie to, uważane słusznie za największe z wielkich sukcesów tego matematyk, opublikował autor w pracy "Podstawy geometrii" (1898). W elementarnym nauczaniu geometrii nie posługujemy się jednak systemem Hilberta, lecz systemem zbliżonym do euklidesowego, gdyż ten pierwszy jest za obszerny i przedstawia zbyt duże trudności logiczne w ścisłym jego stosowaniu. Następny kilkuletni etap pracy Hilberta - to szereg problemów z rachunku wariacyjnego i z teorii równań różniczkowych. W historii twierdzenia Waringa, które głosi, iż dla każdej liczby naturalnej n można dobrać liczbę naturalną k tak ,że dowolna liczba naturalna N jest sumą n-tych potęg k liczb całkowitych nieujemnych, ostatnie słowo przypadło znów Hilbertowi. Twierdzenie to sformułowane zostało w 1782 roku i w treści swojej jest
elementarne. Mimo to przez ponad cały wiek pozostawało bez dowodu. Dopiero w 1909 roku Dawid Hilbert dowód taki podał, opierając się na trudniejszych partiach matematyki wyższej. Pewne osiągnięcia matematyków w teorii równań całkowych skłoniły tego uczonego do zajęcia się tą dziedziną i sprowokowały nowy notowany na kartach historii matematyki sukces. Dodatkowym wynikiem tej pracy było stworzenie i wprowadzenie do matematyki pojęcia znanego obecnie jako "przestrzeń Hilberta". Zaniechawszy równań całkowych, Hilbert wraca do zagadnienia, które uważał za najważniejsze we współczesnej matematyce. Mianowicie do stworzenia logicznych podstaw matematyki. Zagadnieniu temu poświęca Hilbert kilkanaście ostatnich lat swojego życia,dając tym dowód, że do końca wytrwał n a trudnym posterunku i mozolnie krok za krokiem dążył do rozwoju i ujednolicenia pięknej nauki: matematyki. Powrót
JULIUSZ PAWEŁ SCHAUDER(1898-1943) : Lata międzywojenne są okresem szczególnie żywotnym w rozwoju polskiej matematyki. W okresie tym do najważniejszych ośrodków matematycznych należą Warszawa i Lwów. Jednym z najwybitniejszych uczniów szkoły lwowskiej był Juliusz Paweł Schauder. Środowisko lwowskie wywiera duży wpływ na twórczość Schaudera. Najściślej jednak na jego działalności naukowej zaważyła postać Stefana Banacha, którego później był współpracownikiem. Scahuder pozostawał również pod innymi wpływami. Można tu przytoczyć nazwiska Bernsteina i Hadamarda, których badaniami się pasjonował, uogólniając ich wnioski i tworząc metody lepsze od tych stosowanych przez tych uczonych. Jego badania rozciągają się zasadniczo na cztery dziedziny matematyki, studiowane zazwyczaj niezależnie. mimo takiej szerokiej rozciągłości badań, twórczość jego wykazuje wielką ciągłość. Zawsze starał się mimo barier klasyfikujących wiedzę dotrzeć do źródła problemów, stosując często
metody różne od ogólnie przyjętych. Jego niezwykłe zdolności szły w parze z pięknymi cechami charakteru: był bardzo pracowity i dokładny. Nigdy nie narzucał sobie zagadnień, badał te które narzucają się same. Tematem jego pierwszych prac była teoria całki. W pracach tych przede wszystkim rozszerza i uogólnia wyniki, które są już znane; w szczególności rozszerza zakres stosowalności wzoru Stokesa wyrażającego całkę powierzchniową przez objętościową. W pracach tych wykorzystuje pojęcia z zupełnie odrębnej dziedziny matematycznej, topologii. Dziedziną , w której Schauder osiągnął najwybitniejsze wyniki, jest topologia. Szczególnie słynne jest jego twierdzenie o punkcie stałym. Rozpatrzmy to zagadnienie na przykładzie. Weźmy okrąg koła i zapytajmy, czy można przekształcić go w sposób ciągły (tzn. z ewentualnym rozciągnięciem, lecz bez rozrywania)na siebie tak ,by każdy punkt zmienił pierwotne położenie. Oczywiście,że można to zrobić: wystarczy obrócić go o pewien kąt dookoła środka. Gdybyśmy jednak postawili
analogiczne zagadnienie w przypadku tarczy kołowej, to podobny sposób by zawiódł, bo przy obrocie znalazłby się punkt - mianowicie środek - który by swego położenia nie zmienił. Okazuje się,że nie tylko przy obrocie ale przy każdym przekształceniu ciągłym tarczy koła na siebie istnieć musi punkt który swego położenia nie zmieni. Takie samo twierdzenie dotyczy kuli (choćby nawet zniekształconej) w przestrzeni trójwymiarowej, a także wielowymiarowych. Twierdzenie to udowodnił jedne z największych matematyków współczesnych, Holender ,L.E.J. Brouwer, uogólnił je natomiast Schauder na przypadek, gdy odwzorowujemy zbiór wypukły na jego część .W topologii uzyskał jeszcze szereg innych wyników na miarę światową. W roku 1938 za pracę wykonaną wspólnie z matematykiem francuskim, Jean Lerayem otrzymuje wielką nagrodę międzynarodową Prix Malaxa. DO odkryć z topologii nie doprowadziły go jednak badania abstrakcyjne, ale możliwość zastosowania tych wyników do teorii równań różniczkowych cząstkowych. dlatego też już w
następnych pracach rozważa inne zagadnienia, który przykuły jego uwagę,mianowicie równania różniczkowe cząstkowe drugiego rzędu typu eliptycznego i hiperbolicznego, I w tej dziedzinie,nie zważając na bariery odgradzające topologię i równania z powodzeniem wykorzystuje twierdzenia topologiczne uzyskując w ten sposób ważne i interesujące wyniki. Drobek tego uczonego zawarty został w 33 publikowanych pracach - wszedł na stałe do matematyki światowej. W 1943 roku Schauder ginie śmiercią tragiczną z rąk gestapo. Matematyka utraciła w nim genialnego i oryginalnego uczonego, twórcę metody, której doskonałość wskazuje drogę dalszemu rozwojowi nauki. Powrót
STEFAN BANACH(1892-1945) :Życie Stefana Banacha przypada na okres, w którym, w przeciwieństwie do lat wcześniejszych, żyło i tworzyło wielu sławnych matematyków polskich. Z dorobkiem tego okresu wiąże się nierozerwalnie polska szkoła matematyczna, która słusznie zdobyła międzynarodowe uznanie. Stefan Banach urodził się 20 marca 1892 roku w Krakowie i tam też spędził swe dzieciństwo, o którym mamy jedynie skąpe wiadomości. Wiadomo tylko że jego prawdziwe nazwisko brzmi Greczek. Banach zaś to nazwisko praczki u której się wychował i do której został oddany przez ojca, urzędnika krakowskiej Dyrekcji Kolejowej,pochodzącego z góralskiej rodziny z Jordanowa. Swe pochodzenie góralskie Banach często podkreślał. Matka i ojciec nie interesowali się nim. Gdy podrósł udzielał korepetycji. Studiował na Uniwersytecie Jagiellońskim i Politechnice Lwowskiej, ale żadnej z tych uczelni nie ukończył. Po wybuchu wojny wrócił ze Lwowa do Krakowa. Odkrycie jego dla matematyki
zawdzięczamy Hugonowi Steinhausowi, który tak pisze o pierwszym spotkaniu z Banachem i o jego pierwszej pracy naukowej: "Idąc letnim wieczorem roku 1916 wzdłuż plant , usłyszałem rozmowę, a raczej tylko kilka słów; wyrazy całka Lebesgue`a były tak nieoczekiwane ,że zbliżyłem się do ławki i zapoznałem z dyskutantami : to Stefan Banach i Otto Nikodym rozmawiali o matematyce. Powiedzieli mi ,że mają trzeciego kompana Wilkosza... To zagadnienie (mowa o przeciętnej zbieżności sum częściowych rozwinięć Fouriera) postawiłem mu właśnie w roku 1916, gdy zapoznałem się z nim na krakowskich plantach - próbowałem je sam rozwiązać od dłuższego czasu i niemałe było moje zdziwienie, gdy Banach znalazł odpowiedź negatywną, którą zakomunikował mi z pewny zastrzeżeniem, polegało ono na nieznajomości przykładu Du Bois-Reymonda". Praca akademicka Banacha datuje się od 1920 roku. Objął wtedy stanowisko asystenta na Politechnice Lwowskiej. Od tej pory rozpoczyna się jego świetna kariera naukowa. W tym samym 1920 roku przestawia
na Uniwersytecie Lwowskim pracę pt. "Sur les operations dnas les ensembles abstraitis et leur aplication aux equations integrales" ("O operacjach na zbiorach abstrakcyjnych i ich zastosowaniach do równań całkowych").Miała ona pierwszorzędne znaczenie dla analizy funkcjonalnej. Widocznie musiano ją wówczas wysoko ocenić, skoro nadano mu stopień doktora, mimo ,że nie miał ukończonych studiów wyższych. W roku 1922 habilituje się i natychmiast zostaje mianowany profesorem nadzwyczajnym, a w roku 1927 profesorem zwyczajnym. W roku 1939 uzyskuje wielką nagrodę Polskiej Akademii Nauk Umiejętności oraz zostaje wybrany dziekanem na Uniwersytecie Lwowskim i prezesem Polskiego Towarzystwa Matematycznego. ten samouk wszedł do historii matematyki jako główny współtwórca analizy funkcjonalnej, zwanej też teorią operacji (zajmował się również i innymi działami matematyki).Podstawowe pojęcie tej dyscypliny matematycznej stanowi "Przestrzeń Banacha" (nazwa ta pochodzi od Frecheta),a do podstawowych opracowań w tej
dziedzinie należy główne dzieło Banacha - "Teoria operacji",wydana najpierw w języku polskim(1931) a potem we francuskim (1932) jako "Theorie des operations lineaires" i wreszcie w roku 1948 w języku ukraińskim. Książka Banacha dobrze jest znana w światowej literaturze matematycznej, podręcznik ten zawiera przede wszystkim wyniki autora i jego uczniów. Posłuchajmy fragmentu ze wstępu do niego, mówiaego o roli teorii operacji w matematyce:
"Teoria operacji, stworzona przez V.Voltterre`a,zajmuje się badaniem funkcji określonych w przestrzeniach o nieskończeniu wielu wymiarach. Nie ma prawie dziedziny matematyki, gdzie by teoria operacji nie wnikała w sposób istotny. Dość wspomnieć ,że rachunek wariacyjny i teoria równań całkowych okazały się szczególnymi przypadkami ogólnych działów zawartych w tej teorii. Piękność teorii operacji leży głównie w tym, że w niej łączą się w harmonijną całość metody matematyki klasycznej z metodami nauki nowożytnej... Są działy matematyki, których głębsze zrozumienie możliwe jest tylko przy pomocy znajomości teorii operacji. Takimi działami są : teoria funkcji zmiennej rzeczywistej, rachunek wariacyjny itp. Jeśli zwrócimy uwagę na jej piękno, tkwiące w teorii operacji, to pomijając jej liczne zastosowania, (które są nieistotne dla oceny piękna samej teorii) możemy ją słusznie zaliczyć do najpiękniejszych działów matematyki".
Dla określenia sylwetki Banacha jako człowieka oraz stylu jego , oddajmy głos Hugonowi Steinhausowi - przyjacielowi i współpracownikowi Banacha. "Banach został profesorem zwyczajnym w roku 1927,ale ani przedtem ani potem, nie był profesorem w uroczystym tego słowa znaczeniu. Wykładał doskonale, nigdy nie gubił się w szczegółach i nigdy nie pokrywał tablicy skomplikowanym i mnogimi znakami. Nie dbał o doskonałość formy werbalnej, wszelki polor humanistyczny był mu obcy przez całe życie zachowywał pewne cechy krakowskiego andrusa w sposobie bycia i mowy. Sformułowanie myśli na piśmie sprawiało mu duże trudności. Pisał swoje manuskrypty na luźnych kartkach wyrwanych z zeszytu;gdy trzeba było zmieniać część tekstu, wycinał zbędne miejsca i podklejał resztę czystą kartką, na której pisał nową wersję. Gdyby nie pomoc przyjaciół i asystentów pierwsze prace Banacha nigdy byłyby nie dotarły do drukarni. Listów nie pisywał prawie zupełnie i na pytania listowne nie odpowiadał. Nie lubował się w dociekaniach
logicznych choć rozumiał je doskonale, nie pociągały go także praktyczne zastosowania matematyki, choć z pewnością mógłby się nimi zajmować, gdyby chciał - przecież już rok po doktoracie wykładał mechanikę na Politechnice... Banach umiał pracować zawsze i wszędzie. Nie był przyzwyczajony do wygód i nie potrzebował komfortu, więc pensja profesorska powinna mu była wystarczyć. Ale zamiłowanie do życia kawiarnianego i zupełny brak mieszczańskiej oszczędności oraz regularności w prawach codziennych wpędziły go w długi,a w końcu w sytuację bardzo trudną. Chcąc z niej wyjść zabrał się do pisania podręczników. Tak powstał Rachunek różniczkowy i całkowy w dwóch tomach, z których pierwszy wydał Zakład Ossolińskich (1929) a drugi Książnica atlas (1930), ten podręcznik pisany zwięźle i zrozumiale cieszył się i cieszy popularnością wśród studentów szkół wyższych na pierwszych latach studiów. Najwięcej czasu i siły zabrało Banachowi pisanie podręczników arytmetyki, algebry i geometrii dla szkół średnich. Pisał je z
Sierpińskim i Stożkiem, a także sam. Nie było to nigdy kopiowanie już istniejących książek szkolnych; Banach - dzięki swym doświadczeniom korepetytora - zdawał sobie doskonale sprawę ,że każda definicja, każdy wywód i każde zdanie jest problematem dla autora książki szkolnej, który dba o jej wartość dydaktyczną. Moim zdaniem brak było Banachowi jednego tylko z wielu talentów potrzebnych autorowi podręczników szkolnych: umiejętności widzenia przestrzennego. Owoce doświadczeń zebranych podczas wieloletnich wykładów zleconych mechaniki na Politechnice byłą "Mechanika w zakresie szkół akademickich", ten dwutomowy kurs wydany w roku 1938 został wydany powtórnie w roku 1947. Aby zdać sprawę ze znaczenia Banacha dla nauki w ogóle ,a dla nauki polskiej przede wszystkim, trzeba wymienić nazwiska jego uczniów. Widzimy tutaj kilku z nich. Mazur i Orlicz są bezpośrednimi uczniami Banacha;to oni reprezentują dziś w Polsce teorię operacji, ich nazwiska są na okładce "Studia Mathematica" są bezpośrednią kontynuacją
Banachowego programu naukowego, który znalazł wyraz widomy w tym piśmie. Stanisław Ulman, który zawdzięcza Kuratowskiemu inicjację matematyczną, wszedł po doktoracie też w orbitę Banacha. Banach z Mazurem i Ulmanem to był najważniejszy stolik w Kawiarni Szkockiej we Lwowie. Tam odbywały się owe posiedzenia, o których pisze Ulman... ,że "it was hard to outlast or outdrink Banach during these seddions" (trudno było wysiedzieć dłużej albo wypić więcej kawy od Banacha w czasie tych sesji). A była nawet taka sesja która trwała 17 godzin - jej rezultatem był dowód pewnego ważnego twierdzenia z przestrzeni Banacha - ale nikt go nie zapisał i nikt już dziś nie zdoła go odtworzyć... prawdopodobnie blat stolika pokryty śladami chemicznego ołówka został po owej sesji ,jak zwykle ,zmyty przez sprzątaczkę kawiarni. Taki był los niejednego twierdzenia udowodnionego przez Banacha i jego uczniów. Toteż wielką zasługą pani Łucji Banachowej - która spoczywa dziś na wrocławskim cmentarzu - było zakupienie grubego zeszytu w
twardych okładkach i powierzenie go płatniczemu Kawiarni Szkockiej - tam zapisywano zagadnienia, na pierwszych stronicach kolejnych kart, tak ,żeby ewentualne odpowiedzi mogły być kiedyś zapisane na wolnych stronicach obok tekstu pytań. Oryginalna "książka szkocka" była do dyspozycji każdego matematyka, który jej zażądał w kawiarni;niektóre problemy ogłaszano tam z obietnicą nagrody za rozwiązanie - nagrody wahały się od małej czarnej do żywej gęsi. Kto uśmiecha się dziś pobłażliwie, gdy usłyszy o takich sposobach uprawiania matematyki, niech zechce zrozumieć ,że zgodnie ze zdaniem Hilberta, sformułowanie problemu jest połową rozwiązania, a lista nierozwiązanych i ogłoszonych problematów zmusza do do poszukiwania odpowiedzi i jest wyzwaniem dla wszystkich,co chcą mierzyć siły na zamiary - ten stan pogotowia umysłowego stwarza atmosferę naukową... Na późniejsze dzieje Banacha druga wojna światowa rzuciła swój ponury cień. Po wkroczeniu Niemców (z końcem czerwca 1941 roku) musiał stać się karmicielem wszy
w Instytucie Bakteriologicznym profesora Weigla;kilka tygodni spędził w więzieniu, gdyż w jego mieszkaniu zastano osoby trudniące się przemytem marek niemieckich;zanim się sprawa wyjaśniła, zdołał w więzieniu udowodnić pewne nowe twierdzenie. Banach był przede wszystkim matematykiem. Mało go interesowały sprawy polityczne, chociaż sam miał bystre spojrzenie na każdą aktualną sytuację, w której wypadło mu się znaleźć. Przyroda nie robiła na nim żadnego wrażenia; sztuk ,literatura, teatr były dla niego drugorzędnymi rozrywkami, które co najwyżej wypełniały mu, i to rzadko,krótkie przerwy w pracy -cenił sobie natomiast zgrane towarzystwo... Myliłby się kto by wyobrażał sobie Banacha jako marzyciela, abnegata, apostoła czy ascetę. Był to realista, który nawet fizycznie nie przypominał kandydatów na świętych lub choćby świętoszków... Był zdrowy i silny, był realistą aż do cynizmu, ale dał nauce polskiej, a w szczególności matematyce polskiej więcej niż ktokolwiek inny". Powrót
STEFAN MAZURKIEWICZ(1888-1945) : Nazwisko Stefana Mazurkiewicza nie jest może tak dobrze znane szerokiej rzeszy czytelników jak nazwisko np. Newtona, Descartesa czy Eulera, jednakże jest ono dla nas Polaków chyba niemniej ważne. Był on bowiem jednym z twórców i głównych działaczy polskiego ośrodka matematycznego, który zdobył sobie światową pozycję i sławę. Mazurkiewicz urodził się w Warszawie, gdzie jego ojciec był znanym adwokatem. Tam też skończył szkołę średnią. Jako kierunek dalszych studiów wybiera matematykę. Studiuje ją w Krakowie, we Lwowie a następnie w Monachium i Getyndze. W 1913 r. we Lwowie otrzymuje z rąk prof. Sierpińskiego dyplom doktora filozofii za pracę na temat krzywych wypełniających kwadrat. W roku 1915 zostaje profesorem Uniwersytetu Warszawskiego, gdzie będzie pracował aż do końca swojego życia. Był wtedy najmłodszym profesorem wśród grona profesorskiego, a jednocześnie jednym z najbardziej aktywnych. Wraz z Janiszewskim prowadził
seminarium z topologii,które było najprawdopodobniej pierwszym tego rodzaju na świecie. Mazurkiewicz jest jednym z filarów tworzącego się wówczas warszawskiego ośrodka matematycznego, którego zainteresowania idą głównie w kierunku teorii mnogości topologii i podstaw matematyki .Owocem tych zainteresowań jest założenie w 1920 roku przez Mazurkiewicza, Janiszewskiego i Sierpińskiego czasopisma "Fundamenta Mathematicae" poświęcone właśnie tym działom matematyki. Pesymiści twierdzili ,że czasopismo to nie utrzyma się długo z powodu baraku prac w tych nowych dziedzinach matematyki. Jakże się jednak mylili! Warszawski ośrodek, dochodząc do coraz to nowych rezultatów, stawiając i rozwiązując coraz to nowe problemy, zdobywa sobie pozycję o randze światowej i znany jest jako Warszawska Szkoła Matematyczna. Mazurkiewicz jest duszą zebrań współpracującego koła matematyków. Odznaczający się niezwykle głęboką wiedzą, szybką orientacją i wybitną inteligencją, odegrał zasadniczą rolę w kształtowaniu się polskiej
matematyki. W ciągu 9 lat piastuje tytuł dziekana Wydziału Matematyczno-Przyrodniczego, a od 1937 r. jest prorektorem Uniwersytetu. Jest członkiem Polskiej Akademii Nauk, sekretarzem generalnym Warszawskiego Towarzystwa Naukowego oraz przez pewien czas prezesem Polskiego Towarzystwa Naukowego. Opiekuje się również młodzieżą interesującą się matematyką. Jest kuratorem Studenckiego Koła Matematyczno - Fizycznego przy Uniwersytecie Warszawskim, Mimo tych licznych zajęć zawsze znajduje czas na własną pracę naukową, nawet podczas II wojny światowej. Okupację spędza w Warszawie w bardzo ciężkich warunkach. w tym czasie pracuje nad swym głównym dziełem, "Teorią prawdopodobieństwa". Niestety wszystkie rękopisy i notatki dotyczące tej pracy zostały spalone podczas jednego z wielu pożarów wzniecanych przez Niemców. Przez przypadek uratowały się jedynie kopie wielu rozdziałów, przy pomocy których autor odtwarzał swe dzieło w ostatnich latach życia. Wskutek coraz gorszych warunków egzystencji Mazurkiewicz zapada
ciężko na zdrowiu. Po upadku powstania warszawskiego, wypędzony z całą ludnością z Warszawy, zatrzymuje się w Grodzisku. Stan jego zdrowia jest jednak niezwykle ciężki i doskonały matematyk umiera w sile wieku , mając 57 lat. Wkład wniesiony przez Stefana Mazurkiewicza do polskiej matematyki nie ogranicza się tylko do stu trzydziestu prac jakie opublikował. Poprzez szeroko zakrojoną współpracę ze swymi kolegami, poprzez cenne wskazówki i rady, jakie dawał młodszym i mniej doświadczonym uczniom, poprzez głębię swego umysłu i wielkość talentu, idee jakie zasiał w umysłach wielu matematyków, długo jeszcze będą przynosić plony. Powrót
KAZIMIERZ ŻORAWSKI(1866-1953) :Żorawski urodził się 22 czerwca 1866 r. w Szczuczynie w powiecie Ciechanów. Po ukończeniu szkoły średniej zaczyna w 1884 r,. studiować matematykę na Uniwersytecie w Warszawie. Tam też po czterech latach studiów otrzymuje dyplom nauk matematycznych za przedstawioną tezę astronomiczna opartą na własnych obserwacjach. W następnych latach Żorawski kontynuował studia matematyczne w Niemczech na Uniwersytetach w Lipsku i Getyndze. Pobyt w Niemczech ,szczególnie zaś w Lipsku, nadał właściwy kierunek przyszłym jego badaniom. Wykładał tam wówczas Lie, założyciel teorii grup ciągłych, który wywarł wielki wpływ na Żorawskeigo. Pierwsze prace naukowe zawdzięcza właśnie inicjatywie wybitego Norwega i za nie otrzymuje w 1891 roku stopień doktora. Prawie natychmiast, bo już w 1892, jako docent rozpoczyna pracę na Politechnice we Lwowie. W roku 1895 zostaje mianowany profesorem nadzwyczajnym Uniwersytetu Jagiellońskiego w Krakowie. W trzy lata
później zostaje mianowany profesorem zwyczajnym i obejmuje stanowisko dziekana Wydziału Filozofii, a później rektora (1917-1918). wróciwszy do Warszawy w 1919, wykłada kolejno na Politechnice i na Uniwersytecie, aż do emerytury w 1936 roku. w tym też roku został mianowany profesorem honorowym Uniwersytetu Warszawskiego. Umarł 23 stycznia 1953 roku zostawiając wiele cennych rękopisów. Jego zasługi naukowe sprawiły ,że zapraszano go do wielu stowarzyszeń naukowych; był członkiem Polskiej Akademii Nauk i Literatury w Krakowie oraz w Warszawie, był także członkiem Czeskiego Towarzystwa Królewskiego Nauk i Literatury,a w 1951 roku został mianowany członkiem honorowym PAN. Dorobek naukowy Żorawskiego zebrany jest w około 70 pracach i wnosi duży wkład w matematykę światową. Dzieła jego jednakże są mało znane, ponieważ zajmował się on bardzo trudną dziedziną matematyki : niezmiennikami ciągłych grup przekształceń. Najważniejszym jednak osiągnięciem Żorawskiego nie są same abstrakcyjne badania z ciągłymi grupami
przekształceń, lecz ich zastosowanie do różnych innych działów matematyki : przede wszystkim do równań różniczkowych i geometrii oraz w fizyce. Żorawski był pionierem ożywienia twórczości polkich naukowców krakowskiego ośrodka matematycznego. Powrót
TADEUSZ BANACHIEWICZ(1882-1954) : Urodził się w Warszawie. Twórczość naukową zaczął bardzo wcześnie; już jako student nadesłał do Centralnego Biura Astronomicznego w Kilonii telegram z zapowiedzią ,że 19 września 1903 r. planeta Jowisz zakryje gwiazdę stałą BD-6o6191. Po skończeniu uniwersytetu, studiował Getyndze, a następnie od 1910 roku do 1917 pracował jako astronom w Rosji, najpierw w Kazaniu, a potem w Dorpacie. Do Polski przyjechał pod koniec 1918 roku i w marcu 1919 objął stanowisko profesora astronomii Uniwersytetu Jagiellońskiego. Wielki talent naukowy, poparty rzetelną wiedzą , zdobytą w takich ośrodkach jak Getynga i słynne obserwatorium w Pułkowie pod Petersburgiem dał w efekcie astronoma wysokiej klasy, zarówno wybitnego teoretyka jak i badacza .W czasie gdy Banachiewicz objął stanowisko profesora, obserwatorium uniwersytetu było ubogo wyposażone, ale mimo tego potrafił zorganizować badania nad obserwacjami gwiazd zmiennych, które
były wtedy najbardziej aktualną problematyką w astronomii. Do obserwacji tych przyciągnął wielu młodych ludzi. Badania te wywołały żywe zainteresowanie w świecie naukowym i znalazły poparcie ze strony Międzynarodowej Unii Astronomicznej. Jednak o wiele większe zasługi położył Banachiewicz w dziedzinie teoretycznej, a mianowicie stworzył nową teorię matematyczną a mianowicie tzw. rachunek krakowianowy, który znalazł zastosowanie nie tylko w astronomii ale i geodezji i wielu innych dziedzinach nauki. Należy zaznaczyć ,że teoria rachunku krakowianowego wyszła daleko poza zastosowania, dlatego ten wielki astronom Polski nie może być pominięty przy próbach pokazania światowego dorobku matematycznego. Tak np. w wybitnym dziele poświęconym mechanice, wydanym w języku włoskim, autor Beluzzi, omawiając krakowiany, używa zwrotu "con geniale simplicita" (z genialną prostotą) na określenie olbrzymich ułatwień tej metody przy rozwiązywaniu układu równań liniowych z wieloma niewiadomymi w porównaniu z dawnymi metodami
pochodzącymi jeszcze od Gaussa. Dorobek naukowy T.Banachiewicza przekracza liczbę 230 pozycji. Był doktorem honorowym wielu uniwersytetów ,członkiem towarzystw naukowych, między innymi wiceprezesem Międzynarodowej Unii Astronomicznej. Zmarł 17 listopada 1954 roku w Krakowie. Powrót
EMIL BOREL(1871-1956) : Biografia Emila Borela zaczyna się zwykle od słów :matematyk i polityk francuski. Rzeczywiście, jakkolwiek Borel był przede wszystkim znakomitym matematykiem, to wszakże z dużym powodzeniem próbował swych sił na arenie politycznej. Do końca życia pozostawał Borel merem Saint Affrique (Aveyron), gdzie urodził się w roku 1871, oraz radcą generalnym departamentu Aveyrone. Ojciec jego,pastor, dał mu staranne wykształcenie. Emil uczęszczał początkowo do l`Ecole Normale Superieure, potem słuchał wykładów Gastona Darboux i Henri Poincare w College de France, studiując jednocześnie na Sorbonie, w której w 1884 roku uzyskuje doktorat. jego zainteresowania matematyczne skupiają się głównie na rachunku prawdopodobieństwa i teorii funkcji. Obu tym dziedzinom Borel poświęcił większość swoich prac. Wymienimy tutaj "Le hasard", "Traite du calcul des probabilities" i"Monograpfies sur la theorie des Fonctions". Lecz jego "l`Escape et Temps" wskazuje
,że wzorem wielu innych współczesnych mu matematyków, Borela interesowały także zagadnienia fizyczno-filozoficzne. Swoimi pracami wzbogacił szczególnie filozofię nauk ścisłych. Zdolności naukowe łączył Borel ze zdolnościami nauczyciela i organizatora. Wykładając w Lille, w l`Ecole Normal Superieure , i Sorbonie pozostawał jednocześnie od roku 1911 dyrektorem pierwszej z nich, po założeniu zaś Instytutu im Henri Poincare - od 1927 r. jego kierownikiem. Pracując od 1911 prawie wyłącznie w teorii prawdopodobieństwa, wprowadzając w tej dziedzinie nowe i płodne pojęcia, osiągając liczne i ważne rezultaty (np. mocne prawo wielkich liczb), staje się jednocześnie twórcą współczesnej francuskiej szkoły probabilistycznej. Cenne osiągnięcia Borela zostały wysoko ocenione zarówno we Francji , jak i poza jej granicami. Wyrazem tego jest powołanie go na stanowisko przewodniczącego Francuskiej Akademii Nauk, ponadto otrzymał członkostwo licznych akademii zagranicznych i tytuł doktora honoris causa wielu uczelni.
Wspomniane zainteresowania Borela polityką datują się od pierwszej wojny światowej, Karierę swą na tym polu ugruntował piastowaniem urzędu ministra marynarki przez dwie kadencje w rządzie prezydenta Poinleve. Bogate w wydarzenia życie tego człowieka, który tak umiejętnie potrafił pogodzić swą działalność naukową z działalnością pedagoga i polityka, przecięła w 1956 roku śmierć. Powrót
FRYDESZ RIESZ(1880-1956) : Frydesz Riesz (czytaj Ris) już od najmłodszych lat wykazuje duże zainteresowanie matematyka. Po ukończeniu szkoły średniej, na życzenie rodziców, którzy uważali ,że matematyk ma małe szanse na zrobienie kariery, zapisuje się na Politechnikę w Zurychu. Jednak zamiłowanie zwyciężyło i Riesz kończy Uniwersytet w Budapeszcie, a później Uniwersytet w Getyndze. Za rozprawę naukową z geometrii wykreślnej, która mimo cennych wyników nie zwróciła na niego uwagi ówczesnych naukowców, uzyskuje dyplom doktora filozofii. Po uzyskaniu dyplomu nauczyciela Riesz pracuje jako wykładowca w gimnazjum na prowincji, a później w Budapeszcie. Jednocześnie studiuje intensywnie literaturę naukową, poznaje nowe działy matematyki i wydaje szereg publikacji z różnych dziedzin. Jednakże dopiero praca wydana w 1907 roku przyniosła mu rozgłos. W pracy tej zawarł główne tezy nowej teorii, odkrytej później niezależnie przez Ernesta Fiszera i zwanej teorią Riesza-
Fiszera. W 1911 r. Riesz zostaje profesorem nadzwyczajnym na Uniwersytecie w Cluy. W tym okresie opracowuje książkę o układach równań z nieskończoną liczbą niewiadomych (wydana w 1913). W tymże roku uzyskuje tytuł profesora zwyczajnego, a w 3 lata później zostaje członkiem korespondentem Węgierskiej Akademii Nauk. W tym czasie Riesz podejmuje trudną do wykonania pracę zorganizowania Instytutu Matematycznego w Szeged - małym mieście bez naukowych tradycji. Organizuje także wydawnictwo "Acta" - pisma matematycznego odznaczającego się wysokim poziomem naukowym. Wydawane ono było w kraju w języku ojczystym i wielu językach obcych. Marzeniem Riesza było pracować na Uniwersytecie Budapeszteńskim,w ówczesnych jednak warunkach politycznych ten światowej już sławy naukowiec nie może tego zrealizować. Nawet jego kandydatura na członka rzeczywistego Węgierskiej Akademii Nauk zostaje przyjęta w 1936 r. po powtórnym zagłosowaniu. Po zakończeniu wojny Riesz jako jedne z pierwszych wznawia wykłady na Uniwersytecie w Szeged
którego zostaje rektorem i organizuje życie naukowe zniszczone działaniami wojennymi. Gdy w 1946 przyjmuje zaproszenie Uniwersytetu w Budapeszcie na stanowisku profesora,Uniwersytet w Szeged przyznaje mu doktorat honoris causa. Tytuł ten, jako jednynemu z pierwszych przyznaje mu mu także z 70 lecie urodzin Uniwersytet Budapeszteński. Rok wcześniej (w r. 1949) Riesz otrzymał nagrodę "złotą premię Kossuta". Najwyższą nagrodę, "wielką premię Kossuta", uzyskuje w cztery lata później za wydaną w 1952 roku książkę "Wykłady z analizy funkcjonalnej", będącą podsumowaniem wyników jego pracowitego życia. O tym, jakie było znaczenie tej książki, może świadczyć fakt,że została ona wydana w języku francuskim oraz w językach : niemieckim, rosyjskim, angielskim i chińskim. Mimo podeszłego wieku i choroby Riesz nie przestaje pracować. Wykłady prowadzi już siedząc , w notowaniu zaś jego rozważań pomagają mu asystenci. Aż do 1955 roku kieruje życiem naukowy Węgier, zajmując stanowisko przewodniczącego Sekcji Matematyki i Fizyki
Węgierskiej Akademii Nauk. Długoletnią, zadziwiająco aktywną działalność naukową kończy wiosną 1955 r wykładem na posiedzeniu sekcji Matematyczno-Fizyczno -Chemicznej Uniwersytetu Budapeszteńskiego. Odtąd jego życie jest walką ze śmiercią. O tym ,jak pracowitym naukowcem był Riesz, może świadczyć liczba 96 pozostawionych przez niego prac dotyczących głównie analizy funkcjonalnej i teorii topologii. Wielką zasługą Riesza jest także wychowanie licznego pokolenia młodych naukowców węgierskich, którym wpajał swoje ideały i umiłowanie pracy naukowej. Powrót
JOHN VON NEUMANN(1903-1957) :John von Neumann, matematyk niemiecki, inicjator budowy współczesnych maszyn matematycznych, urodził się 28 grudnia 1903 roku w Budapeszcie. Obdarzony był nadzwyczajną pamięcią i od wczesnej młodości wykazywał niezwykłe zdolności i zamiłowanie do nauk ścisłych. Studiował na Uniwersytecie Berlińskim najpierw chemię, następnie matematykę. Odbył też studia w Technische Hochschule w Zurychu i na Uniwersytecie w Hamburgu. Otrzymawszy zaproszenie na wygłoszenie cyklu wykładów na Uniwersytecie w Princeton, wyjechał w 1930 do USA, gdzie pozostał do końca życia. Zainteresowania i publikacje Neumanna obejmowały wiele dziedzin matematyki, ale początkowo miały charakter raczej teoretyczny. Zajmuje się teorią funkcji rzeczywistych,logiką matematyczną, teorią miary,geometrią ciągłą, ogólną topologią, teorią ergodyczności, problemami związanymi z pierścieniami operatorów, teorią kwantów. W pracach nad rachunkiem prawdopodobieństwa interesował
rozwojem teorii gier i matematyki gospodarczej. Pod koniec lat trzydziestych zajmują go problemy hydrodynamiki teoretycznej i w związku z tym poświecił wiele czasu rozwiązaniom równań różniczkowych cząstkowych za pomocą znanych metod analitycznych. W okresie gdy zaczęła świtu zagrażać wojna, Neumann pracuje nad zastosowaniem matematyki w fizyce. W szczególności poświęca się zagadnieniom z hydrodynamiki wzajemnego oddziaływania fal uderzeniowych - niezmiernie ważnego dla celów wojskowych. Zagadnienie to wymagało dużej ilości obliczeń i to ,między innymi, było przyczyną skierowania zainteresowań Neumanna maszynami matematycznymi. Stał się on czołowym znawcą i propagatorem używania elektrycznych maszyn matematycznych do rozwiązywania nierozstrzygniętych jeszcze problemów matematycznych. Zmodyfikował i ulepszył maszynę Eniac, zbudowaną w Filadelfii dla Ballistic Research Laboratories of Army Ordnance. Pracuje w Waszyngtonie ,Los Alamos i innych miejscowościach na terenie USA odbywa wiele kondferencji z uczonymi.
Po wojnie współpracował z grupą wybranych matematyków i inżynierów i zbudował eksperymentalny kalkulator elektronowy w Institute od Advanced Study pod nazwą Joniac. Ciekawe jest ,że opracowanie planu maszyny zostało oparte na pewnych czynnościach mózgu ludzkiego. Neumann specjalnie studiował neurologię oraz psychiatrię, które doprowadziły go do przekonania ,że w maszynach elektrycznych można naśladować pewne uproszczone modelu mózgu ludzkiego. Nawał zajęć sprawia ,że uczony może pisać prace naukowe tylko w nocy lub wczesnym rankiem. Próbował rozwiązać szereg problemów z metrologii za pomocą obliczeń maszyn matematycznych, z których korzystał także przy rozwiązywaniu wielu zagadnień rozwijającej się fizyki jądrowej. Neumann ściśle współpracował z laboratoriami Komisji do Spraw Energii Atomowej, a w 1952 roku został członkiem Ogólnego Komitetu Doradczego AEC. W dniu 15 marca 1955 roku Neumann został zaprzysiężony na stanowisko członka Komisji do Spraw Energii Atomowej i w maju osiedlił się z żoną Klarą na
stałe w Waszyngtonie. W sierpniu tegoż roku nastąpiły pierwsze objawy choroby raka kości. Na początku 1955 r Neumann otrzymał zaproszenie Fundacji Sillimana do wygłoszenia wykładów na Uniwersytecie w Yale w trymestrze wiosennym 1956 roku. Zaproszenie to uważane jest w USA za wybitne wyróżnienie, ponieważ mogą je otrzymać tylko uczeni światowej sławy. Tradycja wymaga wydania wykładów w formie książkowej pod auspicjami Uniwersytetu w Yale. Neumann intensywnie zabrał się do opracowania tematu wykładu i napisał ostatnią swą pracę pt. "Maszyna matematyczna i mózg ludzki". Od stycznia 1956 r. zmuszony jest używać wózka inwalidzkiego,na którym uczestniczy w zebraniach naukowych i w biurze. W początkach kwietnia Neumann zostaje przewieziony do szpitala Waltera Reeda, gdzie mimo zanikania sił w dalszym ciągu pracuje nad przygotowaniem rękopisu, którego niestety nie ukończył. W dniu 8 lutego 1957 r. Neumann zakończył życie , a Uniwersytet w Yale dla uczczenia pamięci wybitnego uczonego wydał drukiem książkę "Maszyna
elektronowa i mózg ludzki" w serii Wykładów Sillimanowskich. Powrót
MIECZYSŁAW BIERNACKI(1891-1959) : 21 listopada 1959 roku w Lublinie zmarł Mieczysław Biernacki. Stratę tę najdotkliwiej odczuł lubelski ośrodek matematyczny. Życie, działalność naukowa i dydaktyczna Biernackiego wiązały się z dwoma miastami uniwersyteckimi : Lublinem i Poznaniem. Urodził się w Lublinie 30 marca 1891 roku w rodzinie inteligenckiej (ojciec był lekarzem i publicystą). Jako uczeń średniej szkoły im. Stanisława Staszica uczestniczył w strajku szkolnym Szkołę ukończył w 1909 roku i w tym samym roku rozpoczął studia chemiczne na Wydziale Filozoficznym Uniwersytetu Jagiellońskiego. Był to okres, gdy pustoszały sale wykładowe a młodzież oddawała się całkowicie życiu ideowo-organizacyjnemu. Atmosfera ta nie pozostała bez wpływu na Mieczysława Biernackiego. Z powodu udziału w akcji protestacyjnej przeciwko wykładom księdza Zimmermanna zmuszony był w roku 1911 przerwać naukę. Po pewnym czasie wyjechał na studia do Paryża. Jednak i tym razem nie mógł
ich ukończyć. Przerwała je I wojna światowa. Wstąpił ochotniczo do armii francuskiej. Był dwukrotnie ranny. Do Polski wrócił z armią gen. Hallera. W roku 1923 uzyskał licencjat (francuski stopień naukowy niższy od stopnia doktora; bywał często bardziej ceniony od doktoratów wielu uniwersytetów innych państw) nauk matematycznych na Sorbonie, a w roku 1928 stopień doktora. Wrócił jednakże do kraju. Po roku pracy asystenckiej na Uniwersytecie Wileńskim zostaje powołany na stanowisko profesora nadzwyczajnego matematyki na Uniwersytecie Poznańskim w 1929 roku. Pracuje tu do wybuchu wojny. Lata okupacji spędza w rodzinnym Lublinie. Po wyzwoleniu brał czynny udział w organizowaniu Uniwersytetu Marii Curie Skłodowskiej w Lublinie, gdzie obejmuje Katedrę Matematyki. W roku 1946 zostaje członkiem korespondentem Polskiej Akademii Umiejętności. Wśród jego uczniów można było wymienić wielu działających matematyków polskich. Terenem prowadzonych przez niego badań naukowych były przede wszystkim teoria funkcji
analitycznych; na tym odcinku pozostawił wiele wartościowych prac. Zajmował się również innymi działami analizy matematycznej. Nazwisko jego jest znane każdemu studentowi wydziałów matematycznych, a to z tej racji ,że jest autorem dwutomowego podręcznika geometrii różniczkowej. Powrót
ALEKSANDER JAKOWLEWICZ CHINCZIN(1894-1959) : Imię współczesnego rosyjskiego matematyka Aleksandra Chinczina znane jest dzięki jego wybitnym osiągnięciom w takich działach matematyki, jak rachuek prawdopodobieństwa, teoria funkcji, metryczna teoria liczb i fizyka statystyczna. nazwisko jego jest ściśle związane z rozwojem radzieckiej szkoły rachunku prawdopodobieństwa. Alekander Chinczin urodził się w 1894 roku w wiosce Kondrowo Medynskiego w guberni kałuskiej, gdzie jego ojciec był inżynierem w papierni. W 1911 roku wstępuje na Wydział Fizyczno-Matematyczny Uniwersytetu Moskiewskiego. Już jako student rozpoczął pracę naukową w Kole Młodych Matematyków,zajmując się teorią funkcji zmiennej rzeczywistej. W 1916 roku kończy studia i w dwa lata później rozpoczyna pracę jako wykładowca Uniwersytetu Moskiewskiego. Wykłady jego dzięki wysokim wartościom naukowym ,niezwykłej jasności i literackiemu opracowaniu szybko stały się magnesem dla łaknących wiedzy studentów.
W 1922 roku powstaje przy Uniwersytecie Instytut Matematyczno-Mechaniczny. Chinczin jest jednym z pierwszych pracowników nowej placówki naukowej. Już w 1927 roku zostaje mianowany profesorem i od tego czasu jego działalność naukowa jest nieprzerwanie związana z Uniwerystetem Moskiewskim. Był kierownikiem Katedry Rachunku Prawdopodobieństwa, następnie Katedry Analizy Matematycznej. W latach 1932-1934 dyrektorem Instytutu Matematyczno-Mechanicznego. W roku 1939 zostaje wybrany na członka Akademii Nauk i rozpoczyna pracę w Instytucie Matematycznym im. Stiekłowa .Za wybitne osiągnięcia naukowe otrzymuje nagrodę stalinowską (1940), Order Lenina, dwa Ordery Czerwonego Sztandaru Pracy i wiele innych odznaczeń i medali. Po powstaniu Radzieckiej Akademii Pedagogiki (1944) pracuje w tej placówce naukowej i jest długoletnim członkiem jej prezydium. Chinczin ogłosił ponad 150 publikacji naukowych, w tym 12 monografii i podręczników. Pierwsza jego praca z rachunku prawdopodobieństwa ogłoszona została w 1924 roku;
podał w niej prawo iterowanego logarytmu dla schematu Bernoulliego. W parę lat później publikuje niezmiernie interesujące prace z zakresu zbieżności szeregów, prawa wielkich liczb i statystyki. W dwu publikacjach z ostatniego okresu jego działalności podaje logiczne definicje pojęć i podstawowe wyniki teorii informacji. Prace te niezmiernie ważne dla szeregu praktycznych obliczeń jeszcze w tym samym roku zostały przetłumaczone i wydane w kilkudziesięciu krajach. W ostatnich latach Chinczin powrócił do matematycznych metod teorii masowej obsługi. Jego pierwsze prace z tej dziedziny datują się jeszcze z 1930 roku , kiedy to jako członek Rady Delegatów otrzymał polecenie pracy w sekcji łączności. Praca ta o wybitnie społecznym charakterze doprowadziła go do bardzo ciekawych wyników zarówno pod względem matematycznym, jak i praktycznym. Przebudowywano wówczas moskiewską centralę telefoniczną na centralę całkowicie zautomatyzowaną. Obliczenia Chinczina znacznie skróciły czas przebudowy, zmniejszyły koszta
i pozwoliły wprowadzić wiele technicznych udoskonaleń. Chinczin opublikował wtedy dwie prace: jedną o najekonomiczniejszym obsługiwaniu przez jednego robotnika kilku stanowisk automatycznej centrali, druga poświęcona była teoria stałej kolejności (tzw. kolejek) Wszystkie swoej prace z teorii masowej obsługi podał Chinczin w 1955 r. Powrót
RONALD AYLMER FISHER(1890-1962) : 29 lipca 1962 roku w Adelajdzie zmarł jedne z twórców nowoczesnej statystyki matematycznej Ronald A. Fisher. Prace jego stanowią największy dorobek wniesiony w tę dziedzinę matematyki w ciągu ostaniach 50 lat. Fisher urodził się w Londynie. Po skończeniu studiów w 1913 roku jest przez kilka lat nauczycielem fizyki i matematyki. Następnie zostaje wezwany do Instytutu Badań Rolniczych w Rothanstet, gdzie opracowuje wyniki licznie przeprowadzanych tam doświadczeń , których nikt przed nim opracować nie potrafił. W 1933 roku zostaje mianowany profesorem Uniwersytetu w Londynie, a dziesięć lat później - profesorem genetyki w Cambridge. Ostatnie trzy lata życia spędza w Adelajdzie, poświęcając się pracy naukowej na uniwersytecie oraz Commonwealth Scientific and Industrial Research Organization (Stowarzyszenie do Badań Naukowych i Przemysłowych). Prace Fishera w dziedzinie statystyki matematycznej obejmują szeroki zakres. Trudno jest
w paru słowach i w popularny sposób pokazać ich problematykę i scharakteryzować doniosłość ich wyników. Spróbujmy jednakże wymienić choć kilka najważniejszych punktów. A więc jednym z najczęściej stosowanych w statystyce testów do sprawdzania zgodności wyników doświadczalnych z wynikami otrzymywanymi na podstawie przyjęcia pewnej hipotezy (tzw. wynikami teoretycznymi) jest test chi-kwadrat, którego twórcą był Pearson. Początkowo ten test był często niewłaściwie stosowany i dopiero Fisher wskazał , kiedy można go stosować i przy jakich założeniach. Stąd zwykle mówi się :"test chi-kwadrat Pearsona-Fishera". Gosset (pseudonim "Student") pokazał ,jak mając kilka pomiarów tej samej nieznanej wielkości można oszacować różnicę pomiędzy średnią z tych pomiarów x a tą wielkością. Fisher zaś podał ścisły dowód prawdziwości teorii Gosseta (stąd nazwa - rozkład Studenta-Fishera) Już w 1921 roku ukazała się praca Fishera "O matematycznych podstawach statystyki teoretycznej", a w 1925 roku "Metody
statystyczne dla doświadczalników". Ta ostatnia praca była zebraniem wszystkich jego dotychczasowych wyników i doczekała się już kilkunastu tłumaczeń i wydań. Następnie ukazuje się "Projektowanie doświadczeń". Idee zawarte w tym dziele zrewolucjonizowały sposób opracowywania wyników w biologii i rolnictwie, przemyśle i medycynie. Zainteresowania Fishera obejmowały również genetykę. Wydana w 1930 roku jego "Genetyczna teoria doboru naturalnego" jest jednym z najwybitniejszych dzieł w tej dziedzinie. Fisher był nie tylko genialnym naukowcem w wymienionych gałęziach wiedzy, ale człowiekiem o niezmiernie szerokich zainteresowaniach i głębokiej wiedzy ogólnej. Fisher znany był ze swej krótkowzroczności. Lecz jak to jest właściwe wielkim ludziom, potrafił z wady tej uczynić zaletę. W młodości jedne z jego profesorów matematyki nauczał go wieczorami geometrii, a ponieważ Fisher nie mógł czytać ani pisać przy sztucznym świetle, lekcje odbywały się bez książek , bez tablicy. W ten sposób młody uczeń wyrobił sobie
w ogromnym stopniu "intuicję" matematyczną, zdolność przewidywania wyników i wyciągania wniosków bez pomocy papieru i ołówka. Do wielu wyników w statystyce dochodził w ten sposób, dając im matematyczne uzasadnienie dopiero później. Ogólnie możemy stwierdzić ,że prace Fishera określają w dużym stopniu kierunek rozwoju współczesnej statystyki matematycznej. Głównym zaś celem jego było zastosowanie statystyki w praktyce, dbałość o to , by służyła człowiekowi. Powrót
JACK SALOMON HADAMARD(1865-1963) : Hadamard studia wyższe pobierał w l`Ecole Normale w Paryżu. W 1892 roku otrzymał tytuł doktora filozofii. Matematyką zajmuje się już wcześnie. W 1896 roku podał całkowity dowód prawa rozmieszczenia liczb pierwszych, które pozwala bez tablic określić z dużym przybliżeniem ilość liczb pierwszych w dowolnym przedziale. W 1897 roku Hadamard został wykładowcą na Sorbonie, w 1900 otrzymał tytuł profesora, a w 1912 powołano go na członka Paryskiej Akademii Nauk. Hadamard występował zdecydowanie przeciwko wszelkim ograniczeniom w wyborze przedmiotu badań i metod matematycznego postępowania. Wydał obszerny i bardzo wartościowy podręcznik geometrii dla szkół średnich. Zajmował się teorią liczb równaniami różniczkowymi, teorią funkcji analitycznych, równaniami fizyki matematycznej. Hadamard był prekursorem analizy funkcjonalnej. W kursie analizy matematycznej znane jest twierdzenie o promieniu zbieżności dla szeregu potęgowego pod nazwą
twierdzenia Hadamarda-Cauchy`ego, a w teorii wyznaczników nierówności dla wartości bezwzględnej wyznacznika. Liczne kontakty naukowe łączyły go z najwybitniejszymi polskimi matematykami, z prof. W.Sierpińskim. Po II wojnie światowej został członkiem zagranicznym Polskiej Akademii Nauk. Powrót
WITOLD POGORZELSKI(1895-1963) :3 stycznia 1963 roku zmarł w Warszawie Witold Pogorzelski, profesor matematyki, kierownik Katedry Matematyki Politechniki Warszawskiej, kierownik Działu Równań Całkowych Instytutu Matematycznego PAN w Warszawie, prezes Warszawskiego Oddziału Polskiego Towarzystwa Matematycznego, doktor honoris causa Politechniki Łódzkiej, członek Łódzkiego Towarzystwa Naukowego. Witold Pogorzelski urodził się 13 września 1895 roku w Warszawie. Studiował na Uniwersytecie w Nancy i w Paryżu. W roku 1919 uzyskał doktorat, a w 1920 habilitował się w Krakowie, w 1921 otrzymał nominację na profesora w Politechnice Warszawskiej, w 1938 roku został wybrany na członka Polskiej Akademii Nauk Technicznych. Od 1920 roku do końca życia prof. Pogorzelski prowadził nieprzerwanie działalność dydaktyczną;przed wojną na Politechnice Warszawskiej, w czasie okupacji na tajnych kompletach Uniwersytetu Warszawskiego, po wyzwoleniu zorganizował i postawił na wysokim
poziomie Katedry Matematyki na Politechnice Łódzkiej, Warszawskiej i Wojskowej Akademii Technicznej w Warszawie. Pracę naukową rozpoczął on w 1915 roku. Jego dorobek naukowy, obejmujący 98 prac , dotyczy następujących dziedzin matematyki : równa całkowych, równań o pochodnych cząstkowych, funkcji analitycznych, fizyki matematycznej i teorii prawdopodobieństwa. Najważniejsze wyniki prof. Pogorzelski uzyskuje w dziedzinie równań całkowych. Stawia on po raz pierwszy w literaturze matematycznej pewne problemy dotyczące równań całkowych i rozwiązuje je bardzo nowoczesnymi metodami w oparciu o twierdzenia topologii i analizy funkcjonalnej. Dorobek naukowy prof. Pogorzelskiego znajduje swój syntetyczny wyraz w jego monografii "Równania całkowe i ich zastosowanie", która odzwierciedliła jego dorobek własny i dorobek kierowanej przez niego szkoły. Dotyczy to w szczególności tomu III, którego aktualność i treść nie mają odpowiednika w krajowej i obcojęzycznej literaturze. W pracach z równań o pochodnych
cząstkowych narzuca sobie badanie trudnych zagadnień, które rozwiązuje w sposób równie systematyczny, jak i precyzyjny. w badaniach cechuje go subtelność analizy i umiejętność operowania szerokim zakresem różnych działów matematyki oraz stałe i uparte poszukiwania prowadzone w tych dziedzinach, które stanowią fundament i podstawę rozwoju nauk technicznych i matematycznych. Z prac dotyczących fizyki matematycznej i teorii prawdopodobieństwa wymienić można :"Badania teoretyczne ilości ciepła otrzymywanego przez ziemię", "Z teorii ruchów powietrza", "O teorii przewodnictwa elektrycznego", "O teorii stratosfery", "Teoria promieniowania i kwantów energii", "Równanie ruchu gazu promieniującego", "Prawdopodobieństwo bezpieczeństwa konstrukcji" i.in. Prace prof.Pogorzelskiego były drukowane w najpoważniejszych czasopismach matematycznych polskich ,rosyjskich, włoskich,. amerykańskich, francuskich i szwedzkich. Ponadto, prof.Pogorzelski opracował 6 podręczników akademickich (łącznie 9 tomów). do zasług naukowych
prof. Pogorzelskiego należy niewątpliwie stworzenie nowej szkoły matematycznej w dziedzinie równań całkowych. Powrót
NORBERT WIENER(1894-1964) :18 marca 1964 roku zmarł nagle w Sztokholmie profesor Norbert Wiener, wybitny matematyk amerykański, twórca nowej dziedziny nauki - cybernetyki. N.Wiener urodził się 26 listopada 1894 roku w Columbia, w stanie Missouri. Ojciec jego,znawca języków słowiańskich, pochodził z Polski. W 1900 roku, po ukończeniu Tufus College, Wiener rozpoczął studia matematyczne na Uniwersytecie w Harvard gdzie w 1913 roku uzyskał stopień doktora filozofii. Następnie studiował w Cambridge i w Getyndze. Od 1932 roku był profesorem matematyki w Instytucie Technologicznym w Massachusetts. Wiener ogłosił wiele cennych prac z matematyki, jednak największe jego osiągnięcia są związane z powstaniem nowej nauki, znanej dziś pod nazwą cybernetyka. Cybernetyka była wynikiem jego prac matematycznych i ścisłej współpracy z uczonymi innych dziedzin, szczególnie zaś duże znaczenie miała współpraca z przyjacielem, meksykańskim fizjologiem Arturem Rosenbluethem
W czasie wojny, zajmując się zagadnieniami obrony przeciwlotniczej ,Wiener zetknął się z wieloma problemami przekazywania informacji i kierowania, analogicznymi z problemami fizjologicznymi. Po II wojnie światowej cybernetyka ukształtowała się już jako samodzielna nauka. Słowo "cybernetyka" pochodzi od Ampere`a, który w 1834 roku tak nazwał naukę o kierowaniu społeczeństwem ludzkim. Czołową pracą N.Wienera jest książka: "Cybernetics or control and communication in the animal and the machine" (Cybernetyka, czyli sterowanie i łączność w zwierzęciu i maszynie) wydana w 1947 roku .Druga z poważniejszych jego prac "The human use of human begins" wydana w polce pod tytułem "Cybernetyka i społeczeństwo" , ukazała się w 1950. Cybernetyka łączy w sobie osiągnięcia wielu nauk : logiki matematycznej, elektroniki, fizjologii oraz nauk społecznych. Połączenie najnowszych osiągnięć tak wielu dziedzin nauki miało nie tylko wielkie znaczenie teoretyczne, ale i duże zastosowanie praktyczne .Wspomnieć tu należy o maszynach
liczących, radarze, encefalografii oraz zagadnieniach celności artylerii przeciwlotniczej. Książki Norberta Wienera , przełożono na wiele języków, cieszą się wszędzie uznaniem specjalistów i powodzeniem wśród szerokich rzesz czytelników. Cybernetyka bowiem jako nauka pokazała swoje wielkie możliwości, stała się niezbędna w wielu dziedzinach nauki i techniki. Powrót
 , w symbolu tym odzwierciedlona jest nie tylko funkcja podcałkowa i zmienna całkowania. ale też sam proces operacji całkowania. temu wielkiemu człowiekowi los spłatał figla .Choć we wszelkiej działalności odznaczał się dążnością do godzenia przeciwnych poglądów, uwikłał się w ostatnich latach swego życia w spór z Newtonem o pierwszeństwo w stworzeniu rachunku różniczkowego. Spór ten był szczególnie rozdmuchiwany przez zwolenników obu uczonych.
Prawda zaś wyglądała chyba tak: pierwsze rezultaty uzyskał Newton. Leibniz do odkrycia doszedł na innej drodze (przy zagadnieniu poszukiwania stycznej do krzywej) i zupełnie samodzielnie. Poza tym rezultaty Leibniza były wcześniej dostępne ogółowi matematyków, bo wcześniej były publikowane. Rachunek różniczkowy Leibniza odznaczał się trafniejszą symboliką i stanowił samodzielny rozdział matematyki, gdy dla Newtona był jedynie środkiem dla rozwiązywania zagadnień z mechaniki. Należy jednak zaznaczyć ,że Leibniz w latach 1673,1676 był w Londynie i zawarł tam znajomość Newtonem. Wspomniany spór zatruł schyłek życia Leibniza. Umarł 14 listopada 1716 roku w Hanowerze. Za trumną szedł tylko jeden wierny jego przyjaciel. akademia Berlińska i Królewskie Towarzystwo Londyńskie przemilczały tendencyjnie śmieć tego wielkiego uczonego.
, w symbolu tym odzwierciedlona jest nie tylko funkcja podcałkowa i zmienna całkowania. ale też sam proces operacji całkowania. temu wielkiemu człowiekowi los spłatał figla .Choć we wszelkiej działalności odznaczał się dążnością do godzenia przeciwnych poglądów, uwikłał się w ostatnich latach swego życia w spór z Newtonem o pierwszeństwo w stworzeniu rachunku różniczkowego. Spór ten był szczególnie rozdmuchiwany przez zwolenników obu uczonych.
Prawda zaś wyglądała chyba tak: pierwsze rezultaty uzyskał Newton. Leibniz do odkrycia doszedł na innej drodze (przy zagadnieniu poszukiwania stycznej do krzywej) i zupełnie samodzielnie. Poza tym rezultaty Leibniza były wcześniej dostępne ogółowi matematyków, bo wcześniej były publikowane. Rachunek różniczkowy Leibniza odznaczał się trafniejszą symboliką i stanowił samodzielny rozdział matematyki, gdy dla Newtona był jedynie środkiem dla rozwiązywania zagadnień z mechaniki. Należy jednak zaznaczyć ,że Leibniz w latach 1673,1676 był w Londynie i zawarł tam znajomość Newtonem. Wspomniany spór zatruł schyłek życia Leibniza. Umarł 14 listopada 1716 roku w Hanowerze. Za trumną szedł tylko jeden wierny jego przyjaciel. akademia Berlińska i Królewskie Towarzystwo Londyńskie przemilczały tendencyjnie śmieć tego wielkiego uczonego. 
 jest jednostką urojoną. Wzór de Movire`a pozwala obliczyć wszystkie wartości n pierwiastków n-tego stopnia z liczby a. Na przykład z liczby 1 istnieją cztery pierwiastki czwartego stopnia, są nimi :1,-1, i, -i. Wiąże się to z zagadnieniem podziału okręgu na n równych części i wy,aga rozwiązania równania cyklotomicznego (równania podziału okręgu). Współczesny zapis wzoru de Movire`a zawdzięczamy Eulerowi .Movire był członkiem Londyńskiego Królewskiego Towarzystwa Naukowego od 1697 roku a także członkiem Paryskiej i Berlińskiej Akademii Nauk. Umarł w Londynie w 1754 roku.
jest jednostką urojoną. Wzór de Movire`a pozwala obliczyć wszystkie wartości n pierwiastków n-tego stopnia z liczby a. Na przykład z liczby 1 istnieją cztery pierwiastki czwartego stopnia, są nimi :1,-1, i, -i. Wiąże się to z zagadnieniem podziału okręgu na n równych części i wy,aga rozwiązania równania cyklotomicznego (równania podziału okręgu). Współczesny zapis wzoru de Movire`a zawdzięczamy Eulerowi .Movire był członkiem Londyńskiego Królewskiego Towarzystwa Naukowego od 1697 roku a także członkiem Paryskiej i Berlińskiej Akademii Nauk. Umarł w Londynie w 1754 roku.