SŁOWNIK MATEMATYCZNY
A B C D E F G H I J K L Ł M N O P R S Ś T U W V X Y Z Ż
SŁOWNIK MATEMATYCZNY - C
całka funkcji : Jedno z podstawowych pojęć analizy matematycznej. Całka ma wielkie zastosowanie w fizyce ,technice, ekonomii i innych naukach. Rozróżniamy całkę nieoznaczoną oraz całkę oznaczoną. Ogólnymi własnościami i sposobami obliczania całek zajmuje się rachunek całkowy.
całka nieokreślona : całka nieoznaczona
całka nieoznaczona (całka nieokreślona) : Pojęcie analizy matematycznej, powstałe na granicy zagadnienia wyznaczenia funkcji F(x), której pochodna róna jest w pewnym przedziale danej funkcji f(x). W wielu konkretnych przypadkach wyznaczanie funkcji F(x) - zwanej funkcją pierwotną funkcji f(x)
jest łatwe. Jeśli znana jest jedna funkcja pierwotna F(x) funkcji f(x), to każda inna jest postaci F(x)+C , gdzie C jest odpowiednio dobraną stałą. Suma F(x)+C, gdzie C jest stałą dowolną, jest więc ogólnym wyrażeniem wszystkich funkcji pierwotnych danej funkcji f(x),zwanym całką nieoznaczoną funkcji f(x) i jest oznaczona symbolem
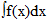
.Mamy więc :
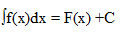
gdzie F(x) jest jakąkolwiek funkcją pierwotną funkcji f(x), zaś C stałą dowolną, zwana stałą całkowania. Metodami obliczania całki nieoznaczonej zajmuje się rachunek całkowy. Udowodniono ,że każda funkcja ciągła f(x) posiada całkę nieoznaczoną.
całka oznaczona : Pojęcie analizy matematycznej. Precyzyjne określenie całki oznaczonej funkcji f(x), ciągłej w przedziale całkowalność funkcji : Istnienie całki tej funkcji w określonym sensie. Cantor Georg (1845-1918) : Matematyk niemiecki, profesor uniwersytetu w Halle. Stworzył teorię mnogości, którą przedstawił w książce "Podstawy ogólnej teorii mnogości" .W 1874 roku dowiódł ,że zbiór wszystkich liczb rzeczywistych jest nieprzeliczalny. W 1878 sformułował ściśle pojęcie mocy zbioru, aksjomat ciągłości i inne. Śmiałe idee
Cantora zostały dopiero po pewnym czasie przyjęte przez ogół matematyków, dzisiaj natomiast są podstawowym instrumentem matematyki. Cantor Moritz (1829-1920) : Niemiecki historyk matematyki, profesor uniwersytetu w Heidelbergu. Napisał fundamentalne dzieło "Wykłady z historii matematyki",obejmujące okres od starożytności do 1799 roku. Caratheodory Constantin (1873-1950) : Matematyk niemiecki pochodzenia greckiego,od 1924 profesor uniwersytetu w Monachium. Zajmował się teorią miary (miary zbioru), teorią odwzorowań konforemnych, rachunkiem wariacyjnym, teorią równań różniczkowych i in. Cardano Geronimo (1501-1576) : Matematyk, lekarz i filozof włoski. Zajmował się m.in algebrą i mechaniką. Jakoe jeden z pierwszych w Europie używał liczb zespolonych i ujemnych pierwiastków równania. Podał przekształcenie liniowe sprowadzające równanie trzeciego stopnia do równania nie zawierającego niewiadomej w kwadracie. Ułożył wzory na pierwiastki
równania trzeciego stopnia w oparciu o wzory pochodzące od Tartaglii i podawał je za własne. Carnot Lazare Nicolas Marguerite zwany Wielkim Carnot (1753-1823) : Francuski matematyk i mąż stanu, organizator armii rewolucyjnej. W dziedzinie matematyki zajmował się podstawami rachunku nieskończenie małych, w geometrii jego metody przyczyniły się do stworzenia geometrii rzutowej. casus irreducibilis : Jeden z przypadków przy rozwiązywaniu równania trzeciego stopnia Cauchy Augustin Louis (1789-1857) : Matematyk i fizyk francuski, od 1816 członek Akademii nauk w Paryżu. Zajmował się różnymi działami matematyki. Największe zasługi położył w analizie matematycznej i teorii sprężystości, której wraz z Navierem był współtwórcą. Jego właściwa sława wynika z osiągnięć w teorii funkcji zmiennej zespolonej i z dążenia do ścisłości
w analizie. Wraz z Gaussem, Abelem i Bolzano należy Cauchy do pionierów nowych wymagań ścisłości w matematyce. W swoich podręcznikach "Wykłady analizy"(1821),"Skrót wykładów z rachunku nieskończenie małych"(1823), "Wykłady z zastosowań analizy do geometrii" oparł się konsekwentnie na pojęciu granicy, podał definicję ciągłości funkcji i całki oznaczonej jako granicy sumy. Stworzył podstawy rachunku różniczkowego
i całkowego, na których opierają się współczesne podręczniki. Twórczość Cauch`ego była tak bogata (ponad 500 prac),że Akademia musiała ograniczyć objętość wszystkich prac przesyłanych do Comptes Rendus aby móc sobie dać radę z samymi jego pracami. Cavalieri Bonaventura Francesco (1598-1647) : Matematyk włoski,uczeń Galileusza, profesor uniwersytetu w Bolonii. Zajmował się geometrią, podał zasadę równoważności figur i brył geometrycznych. Stosowane przezeń metody obliczania pól i objętości czynią go prekursorem rachunku całkowego. Zajmował się też zagadnieniem zamiany ułamków zwykłych na dziesiętne. Cayley Arthur (1821-1895) : Matematyk angielski, profesor uniwersytetu w Cambridge, zajmował się geometrią algebraiczną, teorią wyznaczników, równaniami różniczkowymi. cecha logarytmu : Część całkowita logarytmu danej liczby (tzn. największa liczba całkowita największa od logarytmu tej liczby). Cecha logarytmu dziesiętnego nie mniejszej od 1 jest o 1 mniejsza od liczby cyfr części ułamkowej tej liczby, a liczby mniejszej od 1 jest liczbą ujemną, której wartość bezwzględna równa jest liczbie zer przed pierwszą liczbą znaczącą (wliczając w to i zero przed przecinkiem). cechy podobieństw trójkątów : Twierdzenia podające warunki konieczne i wystarczające na to, ażeby dwa trójkąty były podobne (podobieństwo). Dwa trójkąty są podobne jeśli jest pełniony jeden z warunków: cechy podzielności : podzielność liczb cechy przystawania trójkątów : Twierdzenia podające warunki konieczne i wystarczające przystawania trójkątów (przystawanie figur). Dwa trójkąty są przystające jeśli spełniają jeden z następujących warunków: Chajjam Omar (1048-1123) : Matematyk, filozof i poeta perski. W 1076 prowadził obserwatorium astronomiczne, kierował pracami nad reformą starego kalendarza perskiego, podał sposoby rozwiązywania niektóych równań do trzeciego stopnia włącznie (brał pod uwagę tylko pierwiastki rzeczywiste),zbudował własną teorię prostych równoległych,opartą na założeniach równoważnych postulatowi Euklidesa, zajmował się teorią stosunków, gdzie doszedł do ogólnego pojęcia liczb
rzeczywistych Chasles Michel (1793-1880) : Matematyk francuski, członek Akademii Nauk w Paryżu (od 1839).Zajmował się geometrią, mechaniką i historią matematyki. Jego prace przyczyniły się do rozwoju geometrii rzutowej. Napisał książkę "Kurs geometrii wyższej" Christoffel Elvin Bruno (1829-1900) : Matematyk niemiecki, profesor politechniki w Zurychu, od 1872 profesor uniwersytetu w Strasburgu. Zajmował się między innymi teorią funkcji i teorią równań różniczkowych Chwistek Leon (1884-1944) : Matematyk, filozof, poeta,malarz i teoretyk sztuki, twórca teorii formizmu w malarstwie .W latach 1930-1940 był profesorem logiki na uniwersytecie we Lwowie. chyłomierz : Pochylnik ciało : Pojęcie algebry nowoczesnej. Ciało nazywamy każdy zbiór elementów, w którym określone są 2 działania zwane dodawaniem i mnożeniem, przy czym winny być spełnione następujące warunki: ciało liczbowe : Taki zbiór liczb, do którego wraz z każdymi dwoma jego elementami należy ich suma, różnica, iloczyn i iloraz (z wyjątkiem dzielenia przez 0). Zbiór wszystkich liczb wymiernych jest ciałem liczbowym, podobnie jak zbiór wszystkich liczb rzeczywistych, a także wszystkich liczb zespolonych. Nie jest ciałem liczbowym np. zbiór wszystkich liczb naturalnych ciąg : Jedno z podstawowych pojęć matematyki. Ciąg utworzony z pewnego zbioru elementów (np. liczb ,punktów, prostych , kul itd.)jest określony, jeżeli kolejnym liczbom naturalnym 1,2,3,... zostały jednocześnie przyporządkowane określone elementy a1,a2,a3...,które nazywają się wyrazami ciągu. Ze względu na ilość ich wyrazów rozróżniamy ciągi skończone i ciągi nieskończone. Jeśli wyrazy ciągu są liczbami, to ciąg nazywamy liczbowym. Sposób określania
ciągu może być różnorodny: często podaje się tzw. wyraz ogólny ciągu an kiedy indziej pierwszy wyraz (lub kilka wyrazów) oraz przepis pozwalający obliczyć na jego (lub ich podstawie) następne wyrazy (ciąg określony rekurencyjnie np. ciąg Fibonacciego). Do najbardziej znanych ciągów należą postęp arytmetyczny i postęp geometryczny. ciąg Eulera : Ciąg o wyrazie ogólnym an = n2-n+41; jego 40 początkowych wyrazów daje liczby pierwsze, a41 jest już liczbą złożoną. ciąg Fibonacciego : Ciąg liczbowy określony rekurencyjnie:a1=1,a2=1,an=an-2+an-1 (dla n >= 3). Początkowymi wyrazami ciągu Fibonacciego są 1,1,2,3,5,8,13,21,34... Metodą indukcji matematycznej dowodzi się ,że
ciąg funkcyjny : Ciąg którego wyrazami są funkcje. Ciąg funkcyjny fn(x) n =1,2..., jest określony w pewnym przedziale; jeżeli każdej liczbie naturalnej n przyporządkowana jest pewna funkcja fn(x) określona w tym przedziale. Ciąg funkcyjny fn(x) nazywamy zbieżnym w pewnym przedziale (a,b) do funkcji f(x) zwanej funkcją graniczną lub granicą ciągu, gdy dla dowolnie małej liczby dodatniej e istnieje dla każdego x taka liczba N(zależna od e i x),że ciąg harmoniczny : ciąg nieskończony ciąg malejący : Ciąg liczbowy o tej własności,że każdy wyraz następny jest mniejszy od poprzedniego, tzn an+1 < an ciąg monotoniczny : Ciąg rosnący, ciąg malejący, ciąg nierosnący lub ciąg niemalejący. Każdy ciąg monotoniczny i ograniczony jest ciągiem zbieżnym ciąg niemalejący : Ciąg liczbowy o tej własności ,że każdy wyraz następny jest nie mniejszy od poprzedniego tzn , an+1 > = an dla każdego n. ciąg nierosnący : Ciąg liczbowy o tej własności ,ze każdy wyraz następny jest nie większy od poprzedniego tzn. an+1 = < an dla każdego n ciąg nieskończony : Ciąg w którym, "nie ma wyrazu ostatniego", tzn każdej liczbie naturalnej n odpowiada określony wyraz tego ciągu. Ciąg nieskończony jest np. ciągiem odwrotności kolejnych liczb naturalnych 1, 1/2, 1/3, ..., zwany ciągiem harmonicznym. Udowodniono ,że wszystkie liczby wymierne, a także wszystkie liczby algebraiczne można ustawić w ciąg nieskończony. ciąg ograniczony : Ciąg którego wszystkie wyrazy są co do bezwzględnej wartości mniejsze od pewnej liczby dodatniej M , tzn |an| < M dla każdego n ciąg rosnący : Ciąg liczbowy o tej własności ,że każdy wyraz następny jest większy od poprzedniego tzn. an+1 > an dla każdego n ciąg rozbieżny : Ciąg ,który nie posiada granicy, np. an = (-1)n. Jeżeli dla każdej liczby M > 0 istnieje taka liczba N ,że an > M, gdy n > N, to mówimy ,że ciąg an jest rozbieżny do plus nieskończoności ciąg skończony : Ciąg składający się ze skończonej liczby wyrazów, np. kwadratów kolejnych liczb naturalnych mniejszych niż 100. ciąg stały : Ciąg którego wszystkie wyrazy są jednakowe. Ciąg stały nieskończony jest zbieżny;jego granica równa się wspólnej wartości jego wyrazów ciąg zbieżny : Ciąg posiadający granicę ciąg zwrotny : Ciąg którego wyrazy związane są zależnością an+p+c1an+p-1+c2an+p-2 + cp-1an+1 + cpan =0, gdzie c1,c2,...,cp są to stałe; zależność ta pozwala obliczyć każdy wyraz ciągu, gdy znamy p >=1 pierwszych jego wyrazów. ciągłość funkcji : Klasyczne pojęcie analizy matematycznej. Funkcję f(x) nazywamy ciągłą w punkcie x0, jeżeli dla dowolnie małej liczby dodatniej cięciwa : Odcinek łączący dwa dowolne punkty krzywej lub powierzchni cissoida : cysoida Clairaut Alexis Claude (1713-1765) : Astronom, geodeta i matematyk francuski. Mając 12 lat opracował już pewne własności krzywych czwartego stopnia, w 1731 został adiunktem Akademii Nauk w Paryżu. Napisał wiele cennych prac z teorii równań różniczkowych i geometrii. Badał ruch Księżyca i teorię kształtu Ziemi, przewidział czas powroty komety Haleya. clg : Skót słowa kologarytm constatns (skrót const) : stały, niezmienny continuum : 1.Liczba kardynalna określająca moc zbioru równolicznego ze zbiorem wszystkich liczb rzeczywistych (mówimy ,że ma moc continuum);2. Zbiór mocy continuum;3.Typ przestrzeni topologicznej (spójna i zwarta) cosecans (skrót cosec) : funkcje trygonometryczne cosinus (skrót cos) : funkcje trygonometryczne cosinus hiperboliczny (cos h) : funkcje hiperboliczne cosinusoida : funkcje trygonometryczne cosinusy kierunkowe : Cosinusy kątów pomiędzy wektorem i osiami układu współrzędnych. Cosinusy kierunkowe prostej skierowanej są cosinusami kierunkowymi wektora an tej prostej cotangens : funkcje trygonometryczne cotangens hiperboliczny (ctg h) : funkcje hiperboliczne cotangensoida : funkcje trygonometryczne Courant Richard (1888 - 1972) : Matematyk niemiecki, profesor uniwersytety w Getyndze, a od 1934 w Nowym Jorku. Napisał szereg prac z teorii równań różniczkowych, zajmował się zastosowaniami matematyki w fizyce Cramer Gabriel (1704-1752) : Matematyk szwajcarski , uczeń Johanna Bernouliego i wydawca jego dzieł. Cramer podał ogólne wzory na rozwiązanie układu n równań algebraicznych liniowych z n niewiadomymi (wzory Cramera) i zapoczątkował teorię wyznaczników cyfry : Umowne znaki służące do zapisywania liczb. Już w trzecim tysiącleciu p.n.e. używano w Egipcie hieroglifów do oznaczenia jednostek, dziesiątek itd aż do 107. Innych cyfr używano w Babilonii, a jeszcze innych w starożytnej Grecji i Rzymie, przy czym te ostatnie używane są do dziś. Rozpowszechnione obecnie tzw. cyfry arabskie pochodzą z Indii, swą nazwę zaś zawdzięczają Arabom,którzy sprowadzili je do Europy między X a XIII wiekiem cyfry znaczące danej liczby dziesiętnej : Wszystkie jej cyfry z wyjątkiem początkowych zer oraz zer końcowych, jeżeli nie oznaczają braku jednostek odpowiedniego rzędu , lecz zostały napisane w wyniku zaokrąglenia lub w celu zapełnienia miejsca cykloida : Krzywa płaska, jaką zakreśla punkt okręgu toczącego się bez poślizgu po prostej. Współrzędne dowolnego punktu cykloidy wyrażają się wzorami: cylindroid : Bryła ograniczona powierzchnią walcową, płaszczyzną prostopadłą dop jego tworzących oraz taką powierzchnią S ,że każda prosta równoległa do tworzących powierzchni przebija powierzchnię S co najwyżej w jednym punkcie cysoida (cissoida) Dioklesa : Krzywa płaska, miejsce geometryczne punktów M ,położonych na siecznej okręgu o promieniu a, wychodzącej z początku układu. Równanie cysoidy ma postać Czapłygin Siergiej (1869-1942) : Matematyk rosyjski, profesor matematyki stosowanej uniwersytetu w Moskwie i później w Instytucie Aerohydrodynamicznym, członek Akademii Nauk ZSRR. Napisał wiele prac z mechaniki teoretycznej. Jego prace z dziedziny teorii płata nośnego stanowią podstawę aerodynamiki samolotu czasza kulista : Każdy z dwóch części, na które dzieli powierzchnię kulistą przecinającą ją płaszczyzna. Pole powierzchni czaszy kulistej Czebyszew Pafnutij (1821-1984) : Matematyk i mechanik rosyjski. profesor uniwersytetu w Petersburgu, był członkiem Petersburskiej Akademii Nauk (od 1859) i licznych akademii zagranicznych. Czebyszew jest jednym z twórców petersburskiej szkoły matematycznej. Napisał wiele prac z teorii liczb,rachunku całkowego, rachunku prawdopodobieństwa, teorii mechanizmów itd. część całkowita liczby rzeczywistej : x - liczba całkowita k ,spełniająca warunek , (k =< x < k+1). Np. część całkowita liczby -17,51 to -18, (bo -18 =<-17,51 <-18+1). część ułamkowa liczby rzeczywistej : x - różnica x-k, gdzie k oznacza część całkowitą liczby x. Część ułamkowa jest liczbą nieujemną , mniejszą od 1 czworokąt : Wielokąt płaski o 4 bokach. Suma kątów czworokąta równa się kątowi pełnemu. Jeżeli w czworokącie wypukłym sumy boków przeciwległych są równe, to czworokąt można opisać na okręgu i na odwrót- w czworokącie opisanym na okręgu sumy boków przeciwległych są równe. Jeśli sumy kątów przeciwległych są równe, to na czworokąt można opisać okrąg i na odwrót -w czworokącie wpisanym na okrąg sumy kątów przeciwległych są równe.
Czworokąty dzielą się na równoległoboki, trapezy i trapezoidy. czworościan : Bryła ograniczona 4 ścianami trójkątnymi, ostrosłup, którego podstawą jest trójkąt, Czworościan ograniczony trójkątami równobocznymi (wszystkie krawędzie równe nazywamy foremnym). czwórka harmoniczna : dwustosunek czynnik iloczynu : mnożenie czynnik kwadratowy : Czynnik będący wielomianem drugiego stopnia .Np w iloczynie x(x2+1)(x+1) czynnikiem kwadratowym jest x2+1 czynnik liniowy : Czynnik będący wielomianem co najwyżej pierwszego stopnia. Np. w iloczynie (x-1)(x2+x+1) czynnikiem liniowym jest x-1 czynnik pierwszy : Największy wspólny dzielnik czynnik procentowy : Liczba 1+p/100, gdzie p jest stopą procentową. Czynnik procentowy odgrywa ważną rolę przy obliczaniu procentu prostego oraz procentu składanego.
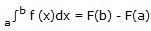
gdzie F(x) jest funkcją pierwotną funkcji f(x).
Interpretacją geometryczną całki oznaczonej jest pole powierzchni ograniczonej prostymi x=a, y=b, krzywą wykresu y=f(x) oraz prostą y=0 (osią odciętych).Pola poniżej osi odciętych mają znak "-". Pojęcie całki oznaczonej uogólnił w 1853 Riemann na przypadek funkcji ograniczonych mających punkty nieciągłości. Dalsze uogólnienie całki oznaczonej
zawdzięcza matematyka Lebesgue`owi.
1.boki jednego trójkąta są proporcjonalne do odpowiednich boków drugiego trójkąta
2.dwa boki jednego trójkąta są proporcjonalne do odpowiednich dwóch boków drugiego trójkąta, a kąty pomiędzy nimi zawarte są równe.
3.dwa kąty jednego trójkąta są równe odpowiednio dwom kątom drugiego trójkąta
Warunki te są również warunkami koniecznymi.
1.boki jednego trójkąta są równe odpowiednim bokom drugiego trójkąta
2.dwa boki i kąt między nimi zawarty jednego trójkąta są równe odpowiednim dwom bokom i kątowi między nimi zawartemu drugiego trójkąta.
3.jedne bok i dwa kąty do niego przyległe jednego trójkąta są równe odpowiedniemu bokowi i dwom kątom do niego przyległym drugiego trójkąta.
W przypadku trójkątów prostokątnych do ich przystawania wystarczy spełnienie jednego z następujących warunków:
1.przyprostokątne jednego trójkąta są równe odpowiednim przyprostokątnym drugiego trójkąta.
2.przyprostokątna i jeden kąt ostry jednego trójkąta są równe odpowiadającej im przyprostokątnej i kątowi ostremu drugiego trójkąta.
3.przeciwprostokątna i jeden z kątów ostrych jednego trójkąta są równe przeciwprostokątnej i jednemu z kątów ostrych drugiego trójkąta
4.przeciwprostokątna i jedna przyprostokątna jednego trójkąta są równe przeciwprostokątnej i jednej z przyprostokątnych drugiego trójkąta
1. a+b = b+q
2. a+(b+c) = (a+b)+c
3.ab=ba
4. a(bc) = (ab)c
5. istnieje element zerowy tzn. taki element 0, ze a+0 = a
6. do każdego a istnieje element przeciwny tzn. taki element (-a) ,że a +(-a)=0
7. istnieje element jednostkowy, tzn taki element 1 ,że a*1 = a
8. do każdego a różnego od zera istnieje element odwrotny, tzn taki element a-1 , że a * a-1 = 1
9. a(b+c) = ab + ac.
Przykładam ciała są np. zbiór wszystkich liczb rzeczywistych i zbiór wszystkich funkcji wymiernych jednej zmiennej o współczynnikach całkowitych.
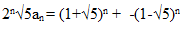 .
.
Ciąg Fibonacciego ma zastosowanie w teorii liczb.
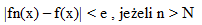
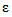 istnieje taka liczba dodatnia
istnieje taka liczba dodatnia 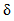 ,że dla każdego x , jeżeli
,że dla każdego x , jeżeli
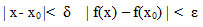
(jest to definicja ciągłości funkcji podana przez Cauchy`ego). Mówimy o funkcji,że jest ciągła w przedziale, jeżeli jest ciągła w każdym punkcji tego przedziału. Przykładami funkcji ciągłych są wielomiany, funkcja wykładnicza, funkcja logarytmiczna,
funkcje sin x i cos x - wszystkie w dziedzinie swej określoności. Warunkiem koniecznym i dostatecznym ciągłości funkcji w punkcie x0, w którym jest ona określona, jest , aby istniała granica funkcji w punkcie x0 i aby była równa wartości funkcji w tym punkcie.. Funkcja , która nie jest ciągła choćby w jednym punkcie, nazywa się funkcją nieciągłą. Funkcja ciągła w przedziale domkniętym
x=r(t- sin t); y=r(1-cos t)
gdzie r oznacza promień toczącego się okręgu, zaś t - miarę łukową kąta, o który okrąg obrócił się podczas toczenia (przyjmujemy t=0 dla x=0). Obrotowi okręgu o kat pełny odpowiada łuk cykloidy którego długość wynosi 8r. Cykloida posiada wiele interesujących własności, wykorzystywanych w życiu praktycznym ;m.in używa się kół zębatych, których zęby mają cykloidalny profil, dający korzystny rozkład sił przy zazębianiu. Używa się także wahadeł cykloidalnych, których okres wahań nie zależy ( w przeciwieństwie do wahadła kołowego)od wielkości początkowego wychylenia
y2 = x3 / 2a-x
jest więc ona krzywą stopnia trzeciego
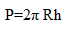 .
.
Ta sama płaszczyzna dzieli kulę na dwie bryły zwane odcinkami kulistymi o objętości
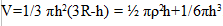 .
.