SŁOWNIK MATEMATYCZNY
A B C D E F G H I J K L Ł M N O P R S Ś T U W V X Y Z Ż
SŁOWNIK MATEMATYCZNY - O
objętość bryły : Liczba rzeczywista nieujemna (liczba wymiarowa objętości)przyporządkowana bryle ograniczonej,spełniająca następujące warunki: obraz jednokładny punktu : jednokładność obraz powinowaty punktu : przekształcenie geometryczne obrót : przekształcenie geometryczne obszar : Zbiór punktów posiadających następujące własności: obszar jednospójny : Obszar , którego brzeg jest zbiorem spójnym. Np. obszarem jednospójnym jest wnętrze koła, wnętrze trójkąta itp. obszar wielospójny : Obszar , który nie jest jednospójny. Np. obszarem dwuspójnym jest wnętrze pierścienia kołowego. obszar wypukły : Obszar ,do którego wraz z każdą parą punktów należy cały odcinek łączący te punkty obwiednia rodziny krzywych (powierzchni) : Krzywa (powierzchnia) styczna w każdym swym punkcie do co najmniej jednej krzywej (powierzchni) z tej rodziny odchylenie standardowe : W rachunku prawdopodobieństwa miara odchylenia wartości zmiennej losowej od jej wartości przeciętnej. Jeżeli zmienna losowa X przybiera wartości x1,x2,...,xn z prawdopodobieństwem p1,p2,...,pn a jej wartość przeciętna wynosi m, to jej odchylenie standardowe oznaczone symbolem σ(X) wyraża się wzorem: odcięta : układ współrzędnych odcinek : Część linii prostej zwarta pomiędzy dwoma różnymi punktami wraz z tymi punktami, które nazywamy końcami odcinka. Jeśli odcinek CD jest przystający (przystawanie figur) do odcinka wyznaczonego przez punkty leżące wewnątrz odcinka AB, to mówimy ,że odcinek CD jest mniejszy od odcinka AB, a odcinek AB jest większy od odcinka CD. Sumą dwóch odcinków (a+b) nazywamy trzeci odcinek c, utworzony przez odłożenie na prostej kolejno odcinków a i b. Mnożenie odcinka przez liczbę k polega na k-krotnym odłożeniu odcinka. Dwa odcinki a i b nazywamy współmiernymi, jeżeli istnieje taki odcinek c, który mieści się całkowitą ilość razy w obu odcinkach; odcinek c nazywamy wtedy wspólną miarą odcinków a i b. Odcinki które nie są współmierne, nazywamy niewspółmiernymi. Jeżeli jedne z odcinków przyjmujemy za jednostkowy (a = 1) to istniej ich wspólną miarą odcinka c ,który mieści się k razy w odcinku a i l razy w odcinku b; liczbę l/k nazywamy miarą lub długością odcinka przy danej
jednostce. Jeśli odcinek b jest niewspółmierny z odcinkiem jednostkowym a , to długość jego określamy za pomocą ciągu obliczeń z niedomiarem i z nadmiarem (dobieramy coraz to mniejszą miarę wspólną odcinka a i coraz to większego odcinka, leżącego wewnątrz bm oraz coraz to mniejszego odcinka wewnątrz którego leży odcinek b).Te ciągi liczb wymiarowych dążą do wspólnej granicy, która jest liczbą niewymierną; jest to miara (długość) odcinka niewspółmiernego. odcinek kołowy : okrąg odcinek kulisty : czasza odejmowanie liczb : Działanie arytmetyczne odwrotne względem dodawania. Odejmując od liczby rzeczywistej a liczbę rzeczywistą b otrzymujemy liczbę rzeczywistą a - b = c, zwaną różnicą a i b, przy czym a nazywamy odjemną, b - odjemnikiem. W zakresie liczb rzeczywistych odejmowanie można zastąpić dodawaniem: a - b = a + (-b).Wprowadza się również odejmowanie wektorów,kątów ,wielomianów itp. odległość dwóch punktów : Długość odcinka łączącego te punkty. Jeżeli punkty mają współrzędne A(x1,y1)i B(x2,y2) to odległość dwóch punktów : odwrotność liczby a ≠ 0 : Liczba 1/a odwzorowanie Z = f(z) : Przekształcenie zbioru D punktów z w zbiór D′ punktów Z Rozpatruje się różne typy odwzorowania w zależności od własności funkcji odwzorowującej f. Jeżeli funkcja f jest ciągła (ciągłość funkcji) to odwzorowanie nazywamy ciągłym, jeżeli funkcja f jest równowartościowa, to odwzorowanie nazywamy odwracalnym lub wzajemnie jednoznacznym. Odwzorowanie nazywamy homeomorficznym jeżeli f jest homeomorfizmem. Ważną rolę w matematyce odgrywają odwzorowania wierne (konforemne) obszaru, których istotną cechą jest fakt ,że nie ulegają zmianie kąty między krzywymi okrąg : Krzywa płaska, zbiór (miejsce geometryczne) wszystkich punktów na płaszczyźnie jednakowo oddalonych od ustalonego punktu zwanego środkiem okręgu. Okrąg dzieli płaszczyznę na dwie części : nieograniczoną i ograniczoną; część ograniczoną, wraz z okręgiem, nazywamy kołem. Prostą ,która przecina okrąg w dwóch miejscach nazywamy sieczną, a jej odcinek zawarty wewnątrz koła (wraz z końcami )nazywamy cięciwą. Najdłuższe cięciwy przechodzą przez środek okręgu, nazywamy je średnicami. Prosta która posiada z okręgiem tylko jeden punkt wspólny jest styczną do okręgu. Odcinek łączący dowolny punkt okręgu ze środkiem nazywamy promieniem okręgu. Promień okręgu przechodzący przez punkt styczności jest prostopadły do stycznej przechodzącej przez punkt. Długość łuku okręgu wynosi 2πr, pole powierzchni koła - 2πr2. Okrąg jest szczególnym przypadkiem elipsy (elipsa równoosiowa).We współrzędnych kartezjańskich równanie okręgu o środku w punkcie O(a,b) i promieniu r ma postać
(x-a)2+(y-b)2 = r2; okręg przedstawiony parametrycznie: x = a +r cosφ, y = b +r sinφ. Cięciwa dzieli koło na dwie części zwane odcinkami kołowymi. Dwa promienie nie pokrywające się dzielą koło na dwie części zwane wycinkami kołowymi. Pole wycinka kołowego P = 1/2φ*r2 = 1/2ł*r = 1/2*ł2/φ gdzie φ oznacza kąt wycinka kołowego (w mierze łukowej), ł - długość łuku, r promień okręgu okres funkcji : funkcje okresowe okres ułamka dziesiętnego : ułamek dziesiętny nieskończony określenie (definicja) : Zdanie składające się z dwóch części połączonych słowami "jest to", znakiem "=", lub " oktaedr : ośmiościan foremny oktylion : nazwa liczby 1048 Orlicz Władysław (1903-1990) : Matematyk polski, profesor Uniwersytetu im. A.Mickiewicza w Poznaniu, członek PAN, zajmował się szeregami ortogonalnymi i zagadnieniami analizy funkcjonalnej, stworzył teorię pewnego typu przestrzeni funkcjonalnych , zwanych "przestrzeniami Orlicza" ortodroma : Powierzchnia kulista ortogonalne trajektorie rodziny linii L : Rodzina linii L′ o tej własności ,ze dowolna linia tej rodziny przecina każdą linię rodziny L pod katem prostym. Np. dla rodziny okręgów o wspólnym środku ortogonalne trajektorie stanowią przechodzące przez ten środek. Jeśli rodzinę L stanowi zbiór rozwiązań równania różniczkowego F(x,y,y′) = 0, to ortogonalne trajektorie będą zbiorem rozwiązań równania różniczkowego F(x,y,-1/y) = 0 ortogonalność : Uogólnienie pojęcia prostopadłości. Obejmuje swoim zakresem prostopadłość prostych, prostych i płaszczyzny, płaszczyzn oraz odpowiednie pojęcie dotyczące wektorów. Dwa wektory w dowolnej przestrzeni liniowej (przestrzeń funkcji) nazywamy ortogonalnymi, jeśli ich iloczyn skalarny równy jest zeru. Dwie podprzestrzenie liniowe nazywamy ortogonalnymi, jeśli każdy wektor jednej z nich jest ortogonalny do każdego wektora drugiej. Ostrogradzki Michał (1801-1861) : Matematyk rosyjski, jeden z twórców petersburskiej szkoły matematycznej, członek Petersburskiej Akademii Nauk, Akademii Nauk w Nowym Jorku,Akademii Nauk w Turynie i członek -korespondent Akademii Nauk w Paryżu. Jest autorem prac z analizy matematycznej, mechaniki teoretycznej, fizyki matematycznej, teorii liczb, algebry i rachunku prawdopodobieństwa. ostrosłup n-kątny : Wielościan, którego jedną ścianą, zwaną podstawą ostrosłupa jest wielokąt o n bokach, a pozostałe ściany są trójkątami posiadającymi jeden wspólny wierzchołek zwany wierzchołkiem ostrosłupa; trójkąty te nazywamy ścianami bocznymi ostrosłupa. Boki podstawy nazywamy krawędziami podstawy, a pozostałe boki trójkątów krawędziami bocznymi ostrosłupa. Wysokość ostrosłupa jest to odległość wierzchołka ostrosłupa od płaszczyzny podstawy. Ostrosłup którego podstawą jest wielokąt foremny i wszystkie krawędzie boczne są równe nazywamy ostrosłupem prawidłowym. W tym ostrosłupie spodek wysokości jest środkiem okręgu opisanego na podstawie. Ściany boczne są trójkątami równoramiennymi; ich wysokości nazywamy apotemami ostrosłupa. Objętość ostrosłupa V=1/3BH, gdzie B jest polem podstawy a h wysokością ostrosłupa. Ostrosłup trójkątny, którego wszystkie boki są równe, nazywamy czworościanem foremnym. Objętość czworościanu foremnego (o krawędzi a)
V= √2/12 a3, pole powierzchni całkowitej S=√3a2, promień kuli opisanej R = √6/4a, promień kuli wpisanej r = √6/12a (R=3r) ostrosłup ścięty : Część ostrosłupa zwarta pomiędzy podstawą i równoległą do niej płaszczyzną przecinającą ostrosłup. Ostrosłup ścięty ma dwie podstawy :górną i dolną. Odległość h pomiędzy podstawami nazywamy wysokością ostrosłupa ściętego. Jego objętość V=1/3h(B1 + √B1*B2 + B2), gdzie B1 i B2 oznaczają pola podstaw ostrosłupa ściętego. Ostrosłup ścięty nazywamy prawidłowym jeśli wszystkie krawędzie boczne są równe, podstawy są wielokątami foremnymi, a ściany boczne trapezami równoramiennymi. Pole powierzchni bocznej ostrosłupa ściętego prawidłowego S=1/2(p1 + p2)h ,gdzie p1 i p2 są obwodami podstaw a h wysokością ścian bocznych oś : Prota na której wyróżniony jest pewien kierunek. Punkt osi możemy przyporządkować liczby rzeczywiste w ten sposób ,że obieramy dowolni punkt odpowiadający liczbie zero i odcinek jednostkowy. Kierunek wzrastających wartości liczbowych zaznaczamy strzałką. Liczby odpowiadające punktom osi nazywamy współrzędnymi kartezjańskimi punktów oś biegunowa : układ współrzędnych oś odciętych : układ współrzędnych oś rzędnych : układ współrzędnych oś stożka : stożek oś symetrii : symetria ośmiościan (oktaedr) : Wielościan foremny o 6 wierzchołkach, 12 krawędziach i 8 ścianach będących trójkątami równobocznymi otoczenie punktu : Każdy zbiór otwarty, który ten punkt zawiera owal Cassiniego : Krzywa płaska, miejsce geometryczne punktów, dla których iloczyn odległości od dwóch ustalonych punktów ,zwanych ogniskami, jest wielkością stałą (F1M * F2M = b2)>Równanie owalu Cassiniego ma postać owal Kartezjusza : Krzywa płaska, miejsce geometryczne punktów, dla których suma odległości r1 i r2 od ustalonych dwóch punktów F1 i 22, zwanych ogniskami, pomnożonych odpowiednio przez ustalone iloczyny m1 i m2, jest stała (m1r1+m2r2 =a). W przypadku m1 = m2 owal Kartezjusza jest elipsą, przy m1 = -m2, hiperbolą. Chasles zauważył ,że owal Kartezjusza ma trzy ogniska, możemy więc podać jeszcze inne określenie: owal Kartezjusza jest miejscem geometrycznym, dla których suma odległości od trzech ustalonych punktów, zwanych ogniskami, pomnożonych odpowiednio przez trzy ustalone liczby, ,jest równa zeru m1r1+m2r2+m3r3 = 0 .Owal Kartezjusza w przypadku ogólnym jest linią algebraiczną czwartego stopnia, której równanie we współrzędnych prostokątnych ma postać :
1.objętość bryły składającej się z brył rozłącznych równa się sumie objętości tych brył.
2.objętości brył przystających są równe.
Przyjmujemy ponadto ,że objętość sześcianu o boku jednostkowym równa się 1. Pojęcie objętości brył znane już było w matematyce starożytnego Wschodu (Babilon, Egipt).Wzory na objętości brył znajdowano empirycznie, dlatego też nie zawsze były dokładne. W "Elementach" Euklidesa i pracach Archimedesa występują już dokładne wzory służące do obliczania objętości wielościanów ,walca, stożka, kuli i części kuli. Objętość bryły określamy za pomocą podejścia do granicy. W daną bryłę wpisujemy sześciany o boku a (tak ,by te sześciany leżały wewnątrz bryły i żadne dwa nie miały wspólnych punktów wewnętrznych) i oznaczamy ich objętość przez W1(a). Zmniejszając krawędź sześcianu, zmniejszamy sumę objętości tych sześcianów; gdy a -> 0 W1(a) dąży do pewnej granicy
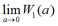 .
.
Jeżeli weźmiemy wszystkie sześciany o krawędzi a, które zawierają chociaż jeden punkt bryły i sumę ich objętości oznaczymy przez W2(a) to przy a -> 0 również W2(a) dąży do pewnej granicy
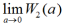 .
.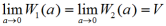
Tę właśnie liczbę V nazywamy objętością bryły. Określona w ten sposób objętość bryły posiada następujące właściwości:
1.po przesunięciu i obrocie nie zmienia się
2.jeżeli jedna bryła leży wewnątrz drugiej, to objętość bryły zewnętrznej jest większa od objętości bryły wewnętrznej. Jeżeli dookoła osi x obracamy obszar ograniczony krzywą y = f(x), osią x i prostymi x= a i x = b to otrzymamy bryłę obrotową, której objętość wyraża się wzorem :
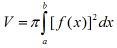 .
.
Jeśli dookoła osi y obracamy obszar ograniczony krzywą x=φ(y), osią y i i prostymi y = a, y =b, to otrzymamy bryłę obrotową o objętości 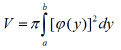
1.wraz z każdym punktem należy do obszaru pewne otoczenie tego punktu (zbiór otwarty)
2.każde da punkty obszaru można połączyć za pomocą linii łamanej całkowicie należącej do tego obszaru (zbiór spójny). Np. obszarem jest zbiór punktów stanowiących wnętrze koła. Jeżeli natomiast dołączymy do tego zbioru punkty leżące na obwodzie koła , to nie będzie on już obszarem, ponieważ warunek 2 nie będzie spełniony. Zbiór składający się z dwu rozłącznych kół nie jest obszarem , bo nie spełnia warunku 2
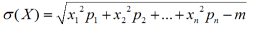
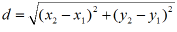
W przestrzeni trójwymiarowej gdzie A(x1,y1,z1)i B(x2,y2,z2) odległość dwóch punktów wyraża się wzorem :
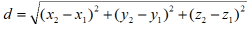 <
<
W przestrzeni n-wymiarowej , gdzie A(x1,x2,...,xn), B(y1,y2,...,yn) odległość dwóch punktów wyraża się wzorem:
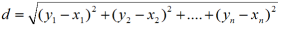
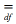 ". Część pierwszą stanowi nazwa przedmiotu określanego (definiendum), drugą wyrażenie określające (definiens), w którym mogą występować wyłącznie tzw. pojęcia pierwotne (znaczenie ich uważane jest za wiadome) oraz pojęcia wcześniej określone w systematycznym wykładzie danej teorii.
". Część pierwszą stanowi nazwa przedmiotu określanego (definiendum), drugą wyrażenie określające (definiens), w którym mogą występować wyłącznie tzw. pojęcia pierwotne (znaczenie ich uważane jest za wiadome) oraz pojęcia wcześniej określone w systematycznym wykładzie danej teorii.
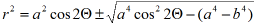
(x2+y2-2rx)2 - s2(x2 + y2) - k = 0, gdzie k, r, s są pewnymi stałymi. Descartes pierwszy podał własności tego owalu i wykazał ,że jest on krzywą aplanatyczną (jest to krzywa oddzielająca dwa ośrodki ,ze promienie świetlne wychodzące z jednego punktu w jednym ośrodku po załamaniu skupiają się też w jednym punkcie)