SŁOWNIK MATEMATYCZNY
A B C D E F G H I J K L M N O P Q R S T U W V Z
SŁOWNIK MATEMATYCZNY - H
half line [półprosta] : Spójny nieograniczonego i właściwy podzbiur linii w przestrzenie euklidesowej.
half plane [półpłaszczyzna] : (1)(Otwarta) Jeden z dwóch zbiorów spójnych pozostający po usunięciu linii z płaszczyzny
(2) (Domknięty) Otwarta półpłaszczyzna, razem z usuniętą linią. Przykład: Na płaszczyźnie kartezjańskiej otwartą półpłaszczyzną jest zbiór {(x,y) : ax + by + c > 0} gdzie (a,b) ≠ (0,0), a i c są stałymi, odpowiednia domknięta półpłaszczyzna jest zbiorem {(x,y) : ax + by + c ≥ 0}
half space [półprzestrzeń] : Jeden z dwóch zbiorów spójnych pozostałych po usunięciu ze sfery jego przecięcia z płaszczyzną przez środek
halting problem [problem zatrzymania] : Nieformalnie, problem zatrzymania pyta czy istnieje skuteczna procedura, która przy danej dowolnej efektywnej procedury i wprowadzonej liczbie naturalnej n, daje odpowiedź "tak" jeśli ten program na wejściu n zatrzymuje się , a na wyjściu "nie" w przeciwnym razie. Formalnie, zbiór zatrzymania K Hausdorffa Zasada Maksimum : Każdy łańcuch w częściowo uporządkowanym zbiorze może być rozszerzony do łańcucha maksymalnego. Zasada ta jest udowodniona w ZFC, i jest udowodniona równoważnie do Akjsomatu Wyboru i Lematu Zorna w ZF Hausdorffa metryka : Niech (X,d) będną przestrzenią metryczną. Jeśli A ⊂ X i ε > 0, niech U(A,ε) będzie ε-otoczeniem A. To znaczy Hausdorffa przestrzeń topologiczna : Przestrzeń topologiczna X taka ,że dla każdej pary różnych punktów x,y ∈ X, istnieje otwarte otoczenie U i V z x i y, odpowiednio, takie ,że U ∩ V = ∅ height (of tree) [wysokość drzewa] : Najmniejsze porządkowe α takie ,że α -ty poziom danego drzewa T jest pusty. To znaczy, α jest pierwszą liczbą porządkową dla której nie ma żadnego w T którego poprzednik miał typ porządkowy α. Na przykład, jeśli T = {{α},{a,b}} jest uporządkowane przez inkluzję, wtedy Lev0(T) zawiera zbiór {α}, Lev1(T) zawiera {a,b} a wysokość drzewa T to dwa.
heptagon [siedmiokąt] : Wielokąt płaski z siedmioma bokami. Siedmiokąt (wypukły) nazywamy regularnym , gdy jego boki mają jednakową długość. W tym przypadku, jego wierzchołki leżą na okręgu a wszystkie krawędzie łączące dwa sąsiednie są jednakowej długości hereditary property of a topological space [własność dziedziczna przestrzeni topologicznej] : Właściwość P przestrzeni topologicznej X taka ,że każda podprzestrzeń A ⊆ X ma właściwość P. hexagon [sześciokąt] : Wielokąt płaski z sześcioma ściankami. hexahedron [sześciościan] : Wielościan z sześcioma ściankami. Najpopularniejszym sześciościanem jest sześcian, foremny dla (wypukłego) wielościanu oznacza m ze wszystkie ścianki są równymi wielokątami foremnymi a wszystkie wierzchołki należą do tej samej liczby ścianek. Hilberta kostka : Iloczyn kartezjański Πn=1∞ I z przeliczalnie wielu przedziałów domkniętych jednostkowych. Jest homeomorficzne do Πn=1∞[0,1/n] jak również podprzestrzeni holomorficzna funkcja : Funkcja holomorficzny loklany układ współrzędnych : Dla zespolonej analitycznej rozmaitości wymiaru n, biholomorficzna identyfikacja ΦU(p) odpowiedniego otwartego otoczenia U(p) każdego punktu p z otwarta kulą o promieniu 1 i środku w początku Cn, ΦU(p) : B0 → U(p) homogeniczna przestrzeń tolpologiczna : Przestrzeń topologiczna X taka ,że ,dla każdej pary punktów x i y w X, istnieje homeomorfizm h: X → X takie ,że h(x) = y homologiczna klasa przekształcenia : Niech f : X → Y będzie ciągła i niech homologia równoważności : Niech T oznacza kategorię wszystkich par (X,A) przestrzeni topologicznych, gdzie X jest identyfikoane z parą (X.∅). Równoważność homotopiczna między parami (X,A) i (Y,B) jest parą funkcji f : (X,A) → (Y,B) i g : (Y,b) & rarr; (X,A) ,takie ,że g o f jest homotopiczne do przekształcenia tożsamościowego iX z X i f o g jest homotopijny to przekształcenia tożsamościowego iY z Y homologii grupa : Niech n będzie dodatnią liczbą całkowitą, X, przestrzenią topologiczną, a x punkt w X. Wtedy n-ta grupa homotopii πn(X,x) jest definiowana jako grupa klas homotopii przekształceń standardowej sfery Sn do X biorąc stały punkt bazowy * Sn do x. W przypadku n = 1, jest to fundamentalna grupa z X (z punktem bazowym x), z konkatenacją pętli obejmujących operację grupy. W wymiarze większym niż 1, operacja grupy okazuje się być przemienna. Inny sposób definiowania πn(X,x) jest pobranie klas homotopii przekształceń [0,1]n do X biorąc granicę do x. Przy tej definicji, łatwo jest zdefiniować operację grupy przez konkatenację : f + g :[0,1]n & rarr; X jest definiowane przez : f + g(t1, t2,
tn) równe f(2t1, t2,
tn) dla 0 ≤ t ≤ ? , i jest równe g(2t1-1, t2,
tn) dla ? ≤ t1 ≤ 1. homologii teoria : Teoria homologii na kategorii T pary przestrzeni topologicznych (X,A) składa się z : homotetia : Transformacja płaszczyzny euklidesowej do samej siebie, która przyjmuje każdy trójkąt do podobnego trójkąta. Homotetia płaszczyzny formuje grupę według złożoności, która zawiera wszystkie izometrie i dylatacje dane przez homotopii typ przestrzeni : Niech T oznacza kategorię wszystkich par (X,A) przestrzeni topologicznych, gdzie X jest identyfikowane przez pare (X,∅). Typ homotopii pary (X,A) jest klasą równoważności Hopfa wiązka : Wiązka S1 → S3 & rarr; S2 formowana naj następuje. Rozważmy S3 jako sfera jednostkowa w C2 (gdzie C oznacza liczby zespolone). Sfera S2 jest dana przez CP1, przestrzeń linii zespolonych w C2 , przez identyfikowanie linii przez punkt (z1, z2) z punktem z2/z1 w C kiedy z1 ≠ 0 i identyfikujemy C ze sferą mniejszą niż jeden punkt; linia zespolona dana przez punkt (0, z2) jest identyfikowana z pozostałymi punktem na S2. Projekcja S3 & rarr; S2 jest dana przez przekształcenie które wysyła (z1, z2) do linii zespolonwje (z1, z2) (myślimy o punkcie CP1 identyfikowanym z punktem w S2) Każde włókno jest homeomorficzne do S1. Używając kwaternionów i liczb Cayleya zamiast liczb zespolonych, można zdefiniować analogiczną wiązkę S7 → S4 i S15 → S8 z wiązką S3 i S7, odpowiednio. Wszystkie trzy wiązki są nazywane wiązkami Hopfa hiperboliczna paraboloida : Jedna z powierzchni kwadratowych w R3. Ponieważ macierz symetryczna nad liczbami rzeczywistymi jest kongruentna do macierzy w postaci diagonalnej, (nie zdegenerowane) powierzchnie kwadratowe są klasyfikowane, przez znak ich wartości własnych i konfiguracji ich punktów w nieskończoności do elispoid, hiperbolid, parabolid eliptycznych i parabolid hiperbolicznych, ostatnia mająca równanie kanoniczne 2z/c = x2/a2 - y2/b2 dla pewnych niezerowych stałych a,b,c. hiperboliczna płaszczyzna : Płaszczyzna spełniająca aksjomaty geometrii hiperbolicznej, która obejmuje aksjomaty Hilberta geometrii płaszczyzny i "charakterystyki aksjomatów geometrii hiperbolicznej": dla dowolnej linii l i punktu p nie na l, istnieją do najmniej dwie linie na p nie napotykające l. Model płaszczyzny hiperbolicznej jest dana przez dysk jednostkowy D = {(x,y) ∈ R2 " x2 + y2 < 1}, z metryką Poincare ds2 = dx2 + dy2/(1-(x2 + y2)/4)2, liniami będącymi geodezyjnymi hiperboloida : Jedna z powierzchni kwadratowych w R3 , jak paraboloida hiperboliczna. Równanie kanoniczne dla hiperboloidy jednopowłokowej : x2/a2 - y2/b2 + z2/c2 = 1 a dla hiperboli dwupowłokowej to : x2/a2 - y2/b2 - z2/c2 = 1, gdzie a,b,c są niezerowymi stałymi. Jak sugeruje nazwa, jedna różnica między tymi dwoma przypadkami jest taka ,że ,ze jedna powierzchnia składa się z jednego komponentu spójnego, a druga z dwóch. hipereliptyczna powierzchnia : Powierzchnia Riemanna X, mianowicie zwartą zespoloną rozmaitość o wymiarze 1, co uogólnia zespolony torus, w poniższym sensie: istnieje holomorficzne przekształcenie → P1 stopnia 2, z 2g + 2 gałęzią punktów gdzie 2-2g jesy charakterystyką Eulera powierzchni topologicznej X. Liczba g jest nazywana genusem powierzchni. Nazywana również krzywą eliptyczna , w przypadku genusu 1 hiperpłaszczyzna : W n-wymiarowej (afinicznej lub rzutowej) przestrzeni wymiaru n, podprzestrzeń o wymiarze n-1. hiperpłaszczyzna w nieskończoność : W n-wymiarowej przestrzeni rzutowej Pm, przy danym systemie współrzędnych (x0 : x1 :
: xn), hiperpłaszczyzna H , zazwyczaj dana równaniem x0 = 0. Dopełnienie Pn\H może być zatem identyfikowane z afiniczną n-przestrzenią An ze współrzędnymi (x1/x0 ,
, xn/x0 hiperprzestrzeń W przestrzeni afinicznej lub rzutowej, podzbiór definiowany przez jedno (niezerowe) algebraiczne równanie we współrzędnych. Hiperpłaszczyzna jest przykładem hiperpowierzchni, która jest definiowana przez jedno liniowe równanie. hypotenuse [przeciwprostokątna] : Bok trójkąta prostokątnego , leżący naprzeciwko kąta prostego. Jest najdłuższym bokiem tórjkąta
U(A, ε) = Ua∈AB(a,ε)
Gdzie B(a,ε) = {x ∈ X : d(x,a) < ε}. Niech H oznacza zbiór wszystkich (nie pustych) domkniętych, ograniczonych podzbiorów z X . Jeśli A,B ∈ H wtedy Metryka Hausdorffa na H jest definiowana przez D(A,B) = inf{ε : A ⊂ U(A,&epsilon) i B ⊂ U(B,ε)}
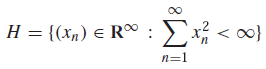
f(z1 ... zn) która jest równa sumie bezwzględnych zbieżnych szeregów potęgowych w odpowiednim policyndrze blisko każdego punktu jej domeny (promień może zależeć od punktu):
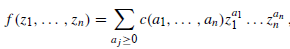
c(a1,
,an) ∈ C. Kiedy n = 1, ten warunek jest równoważny równaniu Cauchy-Riemanna:
∂u/∂x = ∂v/∂y, ∂v/∂y = - ∂v /∂x
dla z = x +iy, f(z) = u(x,y) + iv(x,y).
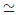 oznacza homotopię relacji równoważności. Klasa homotopi f jest klasą równoważności
oznacza homotopię relacji równoważności. Klasa homotopi f jest klasą równoważności
[f] = {g:X → Y : g jest ciągła i g 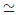 f}
f}
Jeśli A ⊆ X jest podprzestrzenią, wtedy klasa homotopii f rel A jest klasą równoważności [f]A
(i) Funktora Hp X z T do kategorii grup abelowych A dla każdej liczby całkowitej p ≥ 0. Gdzie obraz pary (X,A) jest oznaczony prze Hp(X,A)
(ii) naturalnej transformacji
∂p : Hp>(X,A) & rarr; Hp-1(A)
dla każdej liczby całkowitej p ≥ 0 gdzie A oznacza parę (A,∅) które spełnia aksjomat Eilenberga-Steenroda
f(x,y) = (ax,ay), a ≠ 0
[(X,A)] = {(Y,B) : (Y,B)
jest równoważny homotpoii do (X,A)