SŁOWNIK MATEMATYCZNY
A B C D E F G H I J K L M N O P Q R S T U W V Z
SŁOWNIK MATEMATYCZNY - P
para względnie pierwszych liczb całkowitych : Dwie liczby całkowite których największym wspólnym dzielnikiem jest 1. Na przykład, 6 i 26 są względnie pierwsze, ponieważ gcd(6,25) = 1
parami rozłączne : Kolekcja zbiorów w którym dwa różne zbiory są rozłączne jest rodziną par rozłącznych. Na przykład, {[2n, 2n+1) : n ∈ N} jest zbiorem zbiorów parami rozłącznych (gdzie każdy przedział [2n, 2n+1) jest zbiorem liczb rzeczywistych x takich ,że 2n ≤ x < 2n +1
parami względnie pierwsze liczby : Zbiór liczb całkowitych z taką właściwością taką ,że nie ma dwóch części, ze wspólnym dzielnikiem większym niż 1
parabola : Zbiór punktów na płaszczyźnie jednakowo odległych od danego punktu i danej linii .Alternatywnie, stożkowa, sformowana prze przecięcie stożka kołowego z płaszczyzną taka ,że przecięcie jest spójne ale nie ograniczone
paraboloida : Powierzchnia dana przez zbiór rozwiązań w R3 dla równanie postaci x2/a2 + y2/b2 = z (paraboloida eliptyczna) lub x2/a2 - y2/b2 = z (paraboloida hiperboliczna)
parazwarta przestrzeń topologiczna : Przestrzeń Hausdorffa z taką właściwością ,że każde otwarte pokrycie ma lokalnie skończone otwarte pokrycie, które pokrywa X. Przestrzenie metryczne są parazwarte, ale , oczywiście, generalnie nie zwarte. Parazwartość jest ważna w teorii< rozmaitości ponieważ jest wystarczającym warunkiem w przestrzeni dla zbudowania rozkładu jednoznaczności
parallel [prosta równoległa] : Jednakowa odległość , w pewnym sensie. W przestrzeni euklidesowej, dwie linie są równoległe jeśli się nie przecinają i istnieje płaszczyzna na której obie leżą.
parallelepiped [równolglościan] : Wielościan którego ścianki są równoległobokami.
parallelogram [równoległobok] : Czterościenny wielościan mający równoległe przeciwne boki.
Postulat równoległości : Piąty postulat z Elementów Euklidesa, który mówi ,że jeżeli prosta przecina dwie proste, tworząc dwa kąty wewnętrzne po tej samej stronie o sumie mniejszej niż dwa kąty proste, to te dwie proste przecinają się po tej stronie, po której znajdują się owe kąty wewnętrzne.
partially ordered set [zbiór częściowo uporządkowany] : Zbiór z częściowym uporządkowaniem. Zbiór częściowo uporządkowany jest czasami nazywany poset
partial ordering [uporządkowanie częściowe] : Binarna relacja na zbiorze A (tj. podzbiór A x A), często oznaczona prze ≤ , która jest zwrotna (dla wszystkich x ∈ A, x ≤ x), antysymetryczna (dla wszystkich x,y ∈ A , jeśli x ≤ y i y ≤ x, wtedyu x = y) i przechodnia (dla wszystkich x ,y ,z ∈ A, jeśli x ≤ y i y ≤ z, wtedy x ≤ z). Biorąc pod uwagę częściowe uporządkowanie ≤ na A i x,y ∈ A, x < y definiowane jest x ≤ y i x ≠ y. Zwróć uwagę ,że jeśli ≤ jest częściowym uporządkowaniem na A, wtedy nie jest konieczny przypadek ,że dla każde dwa różne elementy z A są porównywalne.; tj. istnieje wiele x,y ∈ A przy x ≠ y i 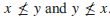
Czasami widzimy alternatywną definicję częściowego uporządkowania, gdzie < jest najpierw definiowane a ≤ definiowane biorąc pod uwagę <. Częściowe uporządkowanie na zbiorze A jest relacją binarną na A ,często oznaczoną prze < , która jest antyzwrotna (dla wszystkich x ∈ A , x < x) i przechodnia .Przy danym częściowym uporządkowaniu < na A i x,y ∈ A, x ≤ y definiuje x < y lub x = y. Używając tej definicji częściowego uporządkowania, można udowodnić ,że &lel jest antysymetryczne. Zauważ ,że jeśli < jest częściowo uporządkowane na A, wtedy nie jest konieczny przypadek ,że każda para różnych elementów jest porównywalna tj. istnieje wiele x,y ∈ A przy x ≠ y i x < y i y < x. Bez względu na wybór definicji < z ≤ lub ≤ z <, odpowiednia notacja z ≤ i < są takie same. Przykładem częściowego uporządkowania jest zwykle uporządkowaniem ≤ na liczbach naturalnych N. To częściowe uporządkowanie jest faktycznie całkowite, lub liniowo uporządkowane. Niech P(N) będzie zbiorem potęgowym zbioru liczb naturalnych; to znaczy, zbiór wszystkich podzbiorów z N. Wtedy zawarcie zbioru ⊆ jest częściowo uporządkowane na P(N) które nie jest liniowo uporządkowany, ponieważ {1,2} i {3} nie są ⊆ - porównywalne;
partial recursive function [funkcja częściowo rekurencyjna] : Wszystkie wspomniane funkcje są funkcjami na liczbach naturalnych N; n-arna funkcja jest częściowa jeśli jej dziedzina jest pewnym podzbiorem z Nn (tj. funkcja może bu być określona na wszystkich danych wejściowych). Pojęcie częściowej funkcji rekurencyjnej jest formalizacją pojęcia intuicyjnie obliczalnej funkcji częściowej. n-arna funkcja częściowa φ jest częściowo rekurencyjna jeśli może być dziedziczona z pewnego zbioru funkcji początkowych przez skończenie wielu zastosowań złożenia, rekurencji lub μ - operatora, tj. istnieje skończony ciąg
φ0,φ1,… φk = φ
funkcji taki, że dla wszystkich i , 0 ≤ i ≤ k
(i)φi jest funkcją początkową
(ii)φi może być uzyskana z {φj : 0 ≤ j < i} przez złożenie, rekurencję lub μ-operator
Poniższe funkcje są funkcjami początkowymi
• S(x) = x+1 (funkcja następnicza)
• Cin(x1,…,xn) = i, dla wszystkich liczb naturalnych i, n ≥ 0 (funkcje stałe)
• Pin(x1,…,xn) dla wszystkich liczb naturalnych n ≥ 1 I 1 ≤ I ≤ n (funkcje rzutowe)
Niech g1,…,gk, f będzie funkcjami n-arnymi i niech h będzie funkcją k-arną; niech x^ oznacza n-krotką x1,…,xn .Funkcja f jest uzyskiwana z g1,…,gk i h będą złożonością jeśli dla wszystkich liczb naturalnych x1,…,xn ,f(x^) = h(g1(x^), … ,gk(x^)). Niech f będzie funckją n-arną, n ≥ 1, g będzie (n-1)-arną funkcją, h będzie (n+1)-arną funkcją, a y^ oznacza (n-1)-krotkę y1,…,yn-1. Funkcja f jest uzyskiwana z g i h przez rekurencję jeśli dla wszystkich liczb naturalnych x, y1,…,yn-1
f(0,y^) = g(y^)
f(x+1, y^) = h(x,f(x,y^),y^)
Niech f bedzie n-arną funkcją i niech g będzie (n+1)-arną (możliwie częściową) funkcją. Niech x^ oznacza n-krotkę x1,…,xn i niech μ będzie operatorem najmniejszej liczby; tj. (μx)[…] oznacza najmniejszą liczbę naturalnę x spełniającą właściwość […]. Niech ↓ będzie skrótem dla zdania "jest określona". Jeśli dla wszystkich liczb naturalnych x1,…,xn
f(x^) = (μy)[g(x^,y) = 0 ∧ (∀z < y)[g(x^,z) ↓ ]]
wtedy f jest uzyskiwana z g przez μ-operator. Jeśli n-arna funkcja jest częściowo rekurencyjna i całkowita (tj. dziedzina funkcji jest całe NN), wtedy funkcja jest nazywana reukrencyją (lub całkowicie rekurencyjną)
Dowolna pierwotna funkcja rekurencyjna jest rekurencyjna; na przykład, funkcja f(x1,x2) = x1 + x2 jest rekurencyjna. Jednakże, nie jest to przypadek, kiedy każda (całkowita) rekurencyjna funkcja jest pierwotnie rekurencyjną. Przykładem funkcji rekurencyjnej ,która nie jest pierwotnie rekurencyjną jest funkcja Ackermanna, która jest definiowana nieformalnie przez "podwójną rekurencję", jak poniżej
A(0,y) = S(y)
A(x+1,0) = A(x,1)
A(x+1,y+1) = A(x,(A(x+1),y))
Funkcja Ackermanna rośnie szybciej niż inne pierwotne funkcje rekurencyjne. Z Hipotezy Churcha-Turinga, intuicjnie obliczeniowa funkcja częściowa jest częściowo rekurencyjna. Funkcja
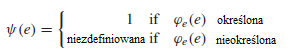
gdzie φe jest funkcją częściowo rekurencyjną z liczbą Gödela e, jest częściowo rekurencyjna
partition [rozkład] : 1. Zbiór. Parami rozłączny zbiór niepustych podzbiorów danego zbioru, którego suma jest danym zbiorem. Na przykład, {{3,a}, {-2}} jest rozkładem zbioru {3,a,-2}. Również {[n,n+1) : n ∈ Z} jest rozkładem z R, (gdzie każdy przedział [n,n+1) jest zbiorem liczb rzeczywistych x takich ,że n ≤ x < n+1)
2.Liczby całkowite. Jeśli n jest dodatnią liczbą całkowitą, rozkład z n jest ciągiem (k1, k2, … , kr) dodatnich liczb całkowitych takich ,że k1 ≥ k2 … ≥ kr a k1 + k2 + … + kr = n. Na przykład (4,3) i (2,2,2,1) są dwoma rozkładami 7
Pascala trójkąt : Specyficzna trójkątna tablica liczb, nazwana na cześć Blaise Pascala. Oto kilka pierwszych wierszy:
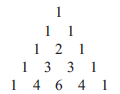
.Jeśli pierwszy wiersz oznaczym jako "wiersz 0" i nazwiemy pierwsze wejście (po lewej) każdego wiersza, wejściem "0-owym", wtedy k-te wejście z n-tego wiersza jest współczynnikiem dwumianowym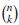
path [droga] : Droga z punktu x do puntu y w przestrzeni topologicznej X jest dowolną funkcją ciągłą f:[0,1] → X przy f(0) = x i f(1) = y. Intuicyjnie, droga jest obrazem funkcji f
Peano przestrzeń : Zwarta, lokalnie spójna przestrzeń metryczna. Z twierdzenia Hahna - Mazurkiewicza, zbiory Peano są dokładnie tymi zbiorami, które występują jako ciągłe obrazy przedziału jednostkowego
Paeano postulaty : Zbiór aksjomatów dla rozwijania właściwości (używając naiwnej teorii mnogości) z liczb naturalnych, Opublikowane w 1899 roku, oparte były na pracy Dedekinda .Jest pięć postulatów Peano
(i)0 jest liczbą naturalną
(ii)Dla każdej liczby naturalnej n, istnieje liczba naturalna n′ , nazywana jest następnikiem n
(iii)Dla każdej liczby naturalnej n, n′ ≠ 0
(iv)Dla dowolnych liczb naturalnych m i n , jeśli m′ = n′ , wtedy m = n
(v)Jeśli I jest dowolnym podzbiorem liczb naturalnych takich ,że
(a)0 ∈ I i
(b)dla dowolnej liczby naturalnej n, jeśli n ∈ I, wtedy n′ ∈ I
wtedy I zawiera wszystkie liczby naturalne
Ten ostatni postulat jest Zasadą indukcji matematycznej i jest stosowany dla każdego z nieprzeliczalnie wielu podzbiorów liczb naturalnych. Postulaty Peano jednoznacznie określają zbiór liczb naturalnych w tym sensie ,że jeśli M jest zbiorem, który spełnia te pięć postulatów (ze zdaniem "n jest liczbą naturalną" zastąpioną przez " n ∈ M"), wtedy M jest zbiorem liczb naturalnych
pedal triangle : Trójkąt wewnątrz danego trójkąta formowany przez połączenie nie wierzchołkowych punktów końcowych wysokości danego trójkąta
Pella równanie : Równanie x2 -dy2 = k, gdzie x i y są z zmiennymi niewiadomymi a d i k są liczbami całkowitymi .Równanie Pella jest przykładem równania diofantycznego (równania dla którego szukamy rozwiązań w liczbach całkowitych lub wymiernych) . Liczba całkowita d jest wolnym kwadratem (to znaczy, jeśli p jest dzielnikiem pierwszym z d, wtedy p2 nie jest dzielnikiem d) i dodatnia ponieważ w przeciwnym razie równanie ma tylko skończenie wiele rozwiązań całkowitych dla x i y.
pęk okręgów : Zbiór wszystkich okręgów na płaszczyźnie przechodzących przez dwa dane punkty
pęk prostych : 1.zbiór wszystkich linii na danje płaszczyźnie przechodzących przez dany punkt; 2.zbiór wszystkich linii równoległych do danej linii
pęk płaszczyzn : Zbiór wszystkich płaszczyzn w przestrzeni zawierających daną linię
pęk sfer : Zbiór wszystkich sfer zawierających dany okrąg
piętnastokąt : Wielokąt mający 15 boków
pięciobok : Wielobok mający pięć boków
pentagonalna liczba : Dodatnia liczba całkowita w postaci 3n2 - n/2 (tj. dowolne wejście w ciągu 1,5,12,22,35, …)
pięciościan : Wielościan z pięcioma ściankami
procent : Z łaciny, "na sto", procenty są używana jako aletrnatywa dla ułamków lub liczb dziesiętnych dla przestawienia proporcji wartości liczbowych
perfect number [liczba doskonała] : Dodatnia liczba całkowita n mając taka właściwość ,że suma jego dzielników dodatnich to 2n, tj. σ(n) = 2n . Zatem 6 jest liczbą doskonałą ponieważ 1+2+3+6 = 2(6). Kolejne dwie liczby doskonałe to 28 i 496. Wszystkie parzyste liczby doskonałe są charakteryzowane jako będące w postaci2p-1(2p-1), gdzie zarówno p i 2p-1 są liczbami pierwszymi (tj. gdzie 2p-1 są liczbami pierwszymi Mersenne′a). Nie istnieją znane nieparzyste liczby doskonałe
perfect set [zbiór doskonały] : Przestrzeń topologiczna X z taką właściwości ,że każdy punkt z X jest punktem skupienia X. To znaczy, przy danym x ∈ X i otoczeniu U z x, zbiór (U ∩ X)\{x} jest niepusty. Wszystkie przedziały linii rzeczywistej są doskonałe. Przykładem podzbioru doskonałego prostej rzeczywiste, który nie jest przedziałem jest zbiór Cantora
perfect square [kwadrat idealny] : Liczba całkowita x dla której istnieje inna liczba całkowita b, taka ,że a = b2. Np. 36 = 62 i 286 = 172 są kwadratami idealnymi
perigon [kąt pełny] : Kąt 360o
perimeter [obwód] : 1.Długość zamkniętej krzywej, szczególnie rozpatrywanej jako granica figury płakiej; 2.Zamknięta krzywa formująca granicę figury płaskiej
periodic continued fraction [ułąmek okresowy łańcuchowy] :
Ułamek w postaci
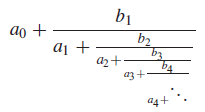
dla którego istnieją dodatnie liczby całkowite p i N takie ,że dla wszystkich k ≥ N. ak+p = ak i bk+p = bk
prostopadła : 1.Względna pozycja pary linii, które przecinają się tak ,że tworzą parę równych kątów przyległych;2.Względna pozycja prostej i płaszczyzny taka ,że prosta jest prostopadła do każdej prostej z którą przecina się na płaszczyźnie; 3.Względna pozycja pary płaszczyzn , które przecinają się tak ,że prosta jest prostopadła zarówno do linii przecięcia i prostej, która jest prostopadła do linii przecięcia
perpendicular bisector [symetralna] : Prosta lub odcinek prostej która przecina dany odcinek i jest do niego prostopadła
pi : Liczba, oznaczona π, równa stosunkowi obwodu i średnicy każdego okręgu. Jest również stosunkiem pola okręgu do kwadratu jego promienia. Wiadomo równiż ,że π jest liczbą przestępną (i dlatego wymierną). Wartość π jest w przybliżeniu równa 3,14159265358979
punkt w nieskończoności : Punkt hiperpłaszczyzny w nieskończoności
polar coordinates [współrzędne biegunowe] : Diwe liczby (r, θ), które określają P na płaszczyźnie (x,y), r będące odległością od początku O a 0 ≤ θ < 2π kątem jaki tworzy półprosta OP z dodatnią osią x, mierzonym w radianach i przeciwny do ruchu wskazówek zegara, z wykątkiem kiedy P = O, co jest powiązane tylko z liczbą zwero; zatem = r cosθ, y = r sinθ. Jeśli r będzie ujemne, para (pr, θ) daje ten sam punkt co para (r, θ + π)
Polska powierzchnia : Przestrzeń topologiczna X , która jest rozdzielna i całkowicie metryzowalna. To znaczy, X ma przeliczalnie gęsty podzbiór i istnieje metryka d indukująca topolgię na X do którego zbieżny jest każdy cig Cuachy′ego. Polskie przestrzenie są naturalnymi ustawieniania dla opisowej teorii zbiorów
Pollarda metoda rho : Metoda rozkładu na czynniki liczb całkowitych złożonych (używając np. jednego z testów pseudopierwszości). Metoda opiera się częściowo na fakcie, że chociaż trudno znaleźć czynniki dużych liczb, stosunkowo łatwo jest (używając algorytmu Euklidesa) znaleźć największy wspólny dzielnik dwóch liczb całkowitych. Niech m będzie dodatnią liczbą całkowitą złożoną i definiujemy ciąg {ui} rekurencyjnie:
(i)u0 = 1
(ii)ui+1 jest jednoznaczną liczbą całkowitą ,taką ,że ui+1 ≡ ui2 + 1 (mod m) i 0 ≤ ui+1 < m
(Generalnie u0 może być liczbą dodatnią całkowitą a ui+1 = f(ui) dla pewnego nieliniowego wielomianu, f). Następnie obliczamy Dn - gcd(u2n - un, m) dla n = 1,2,3,… .Jeśli Dn ≠ 1 dla dowolnego n, wtedy Dn jest dzielnikiem m. Dla zilustrowania, niech m = 1771. Wtedy kilka pierwszych wyrazów ciągu (poczynając od u1 definiowane przez u0 = 1 i ui+1 ≡ + 1 (mod m) to 2,5,26,677,1412, …. Zwróć uwagę ,że gcd(u2 - u1, 1771) = gcd(3,1771) = 1, a gcd(u4 - u2,1771) = gcd(672,1771) = 7, więc 7 jest dzielnikiem 1771 (1771 / 7 = 253. Ponieważ 7 jest liczba pierwszą a 253 liczbą złożoną, możemy powtórzyć metodę Pollarda ,aby wykazać ,że 253 jest iloczynem liczb pierwszych 11 i 23, zatem uzupełniając rozkład na czynniki 1771.
polygonal numer [liczba wielokątna] : Dodatnia liczba całkowita n taka ,że n kropek może być ułożona w określony wielokątny wzór
polynomial [wielomian] : Skończona suma wielokrotności nieujemnych całkowitych potę nieoznaczonego x, ze współczynnikami w danym zbiorze R. Na przykład, 3x5 - 4x3 + x2+ 7x -12, jest wielomianem ze wszpółczynnikami w Z
positive numer [liczba dodatnia] : Liczba rzeczywista , która jest większa od 0
positive orthant [dodatni orthant] : Zbiór punktów (x1 , x2, … , xn) w Rn, takie ,że xi ≥ 0, 1 ≤ i ≤ n. W przypadku płaszczyzny, jest to ćwiartka dodatnia
postulaty Euklidesa : Euklides oparł swoją geometrię na pięciu podstawowych założeniach, znaych jako Postulaty
1. Od dowolnego punktu do dowolnego innego można poprowadzić prostą
2. Ograniczoną prostą można dowolnie przedłużyć
3. Z dowolnego środka dowolnym promieniem można opisać okrąg
4. Wszystkie kąty proste są równe
5. Jeśli dwie proste na płaszczyźnie tworzą z trzecią kąty jednostronne wewnętrzne o sumie mniejszej od dwóch kątów prostych, to te proste, po przedłużeniu, przetną się i to z tej właśnie strony.
power set (of a set) [zbiór potęgowy (zbioru)] : Zbiór wszystkich podzbiorów danego zbioru. Zbiór potęgowy S jest oznaczony przez P(S) lub 2S. Na przykład jeśli S = {3,5} wtedy P(S) = {∅, {3}, {5},{3,5}}. Zbiór potęgowy danego zbioru S, razem z działaniem sumy, części wspólnej i uzupełnianiem w odniesieniu do S, formują algebrę boolowską. Elementy jedności i zera tej algebry boolowskiej są to odpowiednio, S i ∅
predykatów rachunek : Synktatyczna część logiki pierwszego rzędu. Rachunek predykatów jest systemem formalnym składającym się z języka pierwszego rzędu, zbioru dobrze ułożonych formuł, które są nazywane aksjomatami logicznym i listą zasad dedukcji. Formuły dobrze ułożonych, które są aksjomatami logicznymi powinny być poprawnymi formułami. Typowy aksjomat , który może wystąpić w rachunku predykatów to
∀x(α → β) → (∀xα → ∀xβ)
gdzie α i β są formułami dobrze ułożonymi, lub jeśli język zawiera równość
x = y → (α - α′)
gdzie α jest formułą atomową, a α′ jest uzyskiwana z α przez zastąpienie zmiennej x w α w zero lub więcej miejsc przez zmienną y. Typową zasadą dedukcji w rachunku predykatów jest modus ponens. Rachunek predykatów jest używany dla udowadniania tweiordzeń. Podczas gdy rzeczywisty wybór aksjomatów logicznych w zasad dedukcji nie jest ważny, ważne jest ,aby rachunek predykatów było logiczny (tzn. każda dobrze ukształtowana formuła, które jest do udowodnienia w systemie formalnym powinna być logiczną konsekwencją aksjomatów logicznych) i kompletnny (tzn. logiczna konsekwencja logicznych aksjomatów powinna być udowadnialna w systemie formalnym. Rachunek predykatów jest czasem nazywany rachunkiem predykatów pierwszego rzędu
prymarne działanie kohomologiczne : Naturalna transformacja funktorów
Hi(X,A;M) → Hi+j(X,A;N)
może być określone dla wielu wyborów i i j, i wielu wyborów grup abelowych M i N, lub tylko dla określonych wyborów. Działania są często addytywne .Działanie podnoszenia do kwadratu z u do u2 nie jest addytywne; operacje podnoszenia do kwadratu Steenorda (zwane zredukowanymu kwadratami) są addytywne
prime factor [czynnik pierwszy] : Liczba pierwsza p która jest dzielnikiem liczby całkowitej n
prime ideal [ideał pierwszy] : Niech S będzie zbiorem. Ideał I na S jest ideałem pierszym,jeśli dla wszystkich X ⊆ S, albo X ∈ I albo S\X ∈ I
prime number [liczba pierwsza] : 1.Liczba całkowita z dokładnie dwoma dodatnimi dzielnikami całkowitymi (w tym ona sama i 1). Na przykład 5 jest liczbą pierwszą , ponieważ jej dodatnie dzielniki to 1 i 5, podczas gdy 6 nie jest liczbą pierwszą ponieważ dodatnie dzielniki 6 to 1,2,3 i 6. Zauważ ,że 1 nie jest liczbą pierwszą ponieważ ma tylko jeden dodatni dzielnik, samą siebie . 2.Ogólniej, element p pierścienia jest liczbą pierwszą (lub nieredukowalną) jeśli nie ma jedności a wszystkie jego dzielniki (w pierścieniu są sprzężone (wielokrotności jedności) z p
Prime Number Theorem [Twierdzenie o liczbach pierwszych] : Jeśli π(x) oznacza liczbę liczb pierwszych mniejszych lub równych dodatniej liczbie rzeczywistej x, wtedy
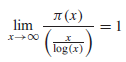
To znaczy, jeśli x jest duże, π(x) ≈ x/log(x). Równoważnie sformułowane twierdzenie mówi, że
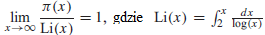
(tzw. całka logarytmiczna). Twierdzenie o liczbach pierwszych zostało udowodnione, niezależnie przez Jaquesa Hadamrda i Charlesa de la Valee Pousiina w 1896 roku
pierwotna funkcja rekurencyjna : Wszystkie wymienione funkcje są funkcjami na liczbach naturalnych. Dowolna n- arna funkcja f jest pierwotnie rekurencyjna jeśli może być wyprowadzona z pewnego zbioru funkcji początkowych przez skończenie wiele zastosowań złożoności i rekurencji; tzn. istnieje skończony ciąg principal curvature [krzywizna główna] : Jeśli P jest punktem na powierzchni S w R3 wtedy krzywizna główna przy P są wartościami minimalnymu i maksymalnymu krzywizny krzywej formowanej przez przecięcie S z płaszczyzną przez P zawierającą wektor normalny do powierzchni przy P. Równoważnie, krzywizny główne są wartościami własnym przekształcenia Weingartena przy P principle fibre bundle [główna wiązka włóknista] : Wiązka włóknista, której włókno jest grupą topologiczną G a której grupa struktury to również G, działając na sobie przez (lewostronne) mnożenie. Składa się z przestrzenie bazowej B, przestrzeni całkowitej E i odwzorowania rzutowego π E → B. Istnieje pokrycie B przez zbiory otwarte Ui i homeomorfizmy Φi : Ui x G → π-1(Ui) takie ,że π o Φi(x,q) = x. To identyfikuje π-1(x) z G jako przestrzeń topologiczna. Przykłady głównych wiązek włóknistych są skonstruowane przez wzięcie odwzorowania ilorazowego π : L → (L/G) z grupy Liego L do przestrzeni ilorazowej z L przez domkniętą podgrupę G. Uniwersalne odwzorownie pokrywające π :E → B jest główną wiązką z fundamentalną grupą z B (z topologią dyskretną) jako wiązka i grupa principal ideal [ideał główny] : Niech S będzie niepustym zbiorem I niech P(S) będzie zbiorem potęgowym z S. Ideał I na S jest ideałem głównym jeśli istnieje zbiór A ⊆ S taki ,że I = {X ∈ P(S) :X ⊆ A} principal type [typ główny] : Typ Φ(x^) teorii T w języku L, taki ,że istnieje L-formuła θ(x^) w Φ(x^) taka ,że T |- ∀x^(θ(x^) → φ(x^)) dla każdego φ(x^) ∈ Φ(x^). To znaczy, pod T, pojedyncza formuła θ generuje zbiór całkowity Φ principal ultragfilter [ultrafiltr główny] : Ultrafiltr U nas algebra boolowską B taki ,że istnieje b ∈ B takie ,że U = {x &isisn; B : b ≤ x} principle of dependent choices [zasada wyborów zależnych] : Załóżmy ,że R jest binarną relacją na niepustym zbiorze S i ,że , dla każdego x ∈ S, istnieją y ∈ S takie ,że (x,y) ∈ R. Wtedy istnieje przeliczalny ciąg x0, x1 principle inclusion-exclusion [zasada włączenia-wyłączenia] : Kombinatoryczna formuła dla kardynalności sumy skończonego zbioru ,zbiorów skończonych/. W przypadku dwóch zbiorów, formuła to |A ∪ B| = |A| + |B| - |A ∩ B| Dla r dowolnie skończonych zbiorów A1>, …, Ar formuła ta to: product [iloczyn] : Ogólny termin używany dla wyniku uzyskanego przez zastosowanie jakiejś operacji, zwykle nazywanej mnożeniem. Na przykład iloczyn liczb naturalnych, iloczyn liczb zespolonych, iloczyn funkcji rzeczywistych, iloczyn kartezjański zbiorów, iloczyn macierzy, iloczyn liczb kardynalnych, iloczyn elementów grupy, iloczyn obiektów w kategorii product bundle [iloczyn wiązki] : Utworzony przez wzięcie iloczynu tensorowego włókien (dwóch wiązek wektorowych E i E′ nad B) nad każdym punktem B. Zatem, iloczyn tensorowy dwóch wiązek prostych jest ponownie wiązką prostych. Wiązki prostych nad przestrzenią formują grupę w odniesieniu do tego iloczynu; grupa tożsamościowa jest wiązką trywialną B x R → B product category [kategoria iloczynowa] : Niech C1, … ,Cn będą kategoriami. Iloczyn C1 x … x Cn jest kategorią której obiekty są n-krotkami (A1, … ,An), gdzie każde Ai jest obiektem Ci , a morfizmy są n-krotkami (f1, … ,fn) z każdym fi jako morfizmem Ci; złożenie morfizmu definiuje składowe : (f1, … ,fn) o (g1, … ,gn) = (f1 o g1 ,… fn o gn) .Iloczyn dowolnej liczby kategorii jest definiowany podobnie product metric [metryka iloczynowa] : Metryka na skończonym iloczynie przestrzeni metrycznych definiowana jest przez wzór product of cardinal numbers [iloczyn liczb kardynanych] : Iloczyn pewnych liczb kardynalnych jest liczbą kardynalną, która jest równoliczna z iloczynem kartezjańskim danych liczb kardynalnych. Jeśli κ i λ są liczbami kardynalnymi, κ ⋅ λ oznacza ich iloczyn kadynalny products of objects [iloczyn obiektów] : Załóżmy ,że C jest kategarią a {Ai : i ∈ I} jest rodziną obiektów C, gdzie I jest pewnym zbiorem indeksowanym . Niech pi : A → Ai będzie morfizmem dla każdego i ∈ I. Krotka (A;pi : i ∈ I) jest iloczynem tej rodziny, jeśli , dla każdego obiektu B z C i każdego zbioru morfizmów fi : B → Ai, dla i ∈ I, istniej jednoznaczny morfizm f : B → A taki ,że pi o f = fi , dla wszystkich i &sin; I. Morfizmy pi są zazwyczaj nazywane morfizmami rzutowymi product space [przestrzeń ilorazowa] : Iloczyn kartezjański dowolnego zbioru przestrzeni topologicznych {Xα}α ∈ A z topologią iloczynową product topology [topologia produktowa] : Standardowa topologia dla iloczynu ∏αXα przestrzeni topologicznych. Podstawa jest dana przez zbiórw postaci ∏αUα gdzie Uα jest otwartym podzbiorem z Xα i Uα = Xα dla wszystkich ale skończenie wielu wskaźników α. Topologia produktowa jest topologią najmniejszą w przestrzeni iloczynowej, co tworzy wszystkie odwzorowania rzutowe ciągłymi projection map [odwzorowanie rzutowe] : Odwzorowanie pα z iloczynu kartezjańskiego ∏αXα przestrzeni topologicznych do Xα, definiowane dla każdego α, przez pα({xα}) = xα projective geometry [geometria rzutowa] : System aksjomatyczny wyrosły z rysunku perspektywicznego z okresu Renesansu; jeden charakterystyczny aksjomat mówi ,że dowolne dwie proste na płaszczyźnie rzutowej mają dokładnie jeden punkt wpsólny. Analitycznie, przestrzeń rzutowa Pn wymiaru n może być dana przez współrzędne rzutowe (x0 : … : xn), które określają punkt do przeskalowania (λx0 : … : λxn) przez niezerową liczbę λ, i spełnia warunek ,że co najmniej jedno xi jest niezerowe. Zatem, zbiór prostych zawierających początek w R3 daje model dla płaszczyzny rzutowej P2 .W niej, proste odpowiadają płaszczyznom przez punkt początkowy i punkt przecięcia prostej wspólnej dwó płaszczyzną projective set [podzbiór rzutowy] : Podzbiór rzutowy fomuje rozszerzoną hierarchię hierarchii Borela w przestrzeni polskiej X. Niech &sum:11 oznacza zbiór wszystkich zbiorów analitycznych w X. Dla n ≥ 1 niech proof [dowód] : W logice pierwszego rzędu, niech L będzie językiem pierwszego rzędu i rozważmy określony rachunek predykatów dla L, z Λ zbiorami logicznych aksjomatów. Niech α będzie dobrze ułożon formuła z L. Dowód z α w rachunku predykatów jest ciągiem α1, α2, … , αn dobrze ułożonych formuł z L takim ,że αn = α i taki ,że dla wszystkicj i , 1 ≤ i ≤ n albo proper fraction [ułamek właściwy] : Dodatnia liczba wymierna a/b gdzie a I b są dodatnimi liczbami całkowitymi i a < b. Na przykład 15/38 jest ułamkiem właściwym, podczas gdy 15/8 jest ułamkiem niewłaściwym properly discontinuous transformation group [właściwa nieciągła grupa transformacji] : Grupa G działająca właściwie nieciągle w przestrzeni X, jeśli dla każdego x w X, istnieje otwarte otoczenie U, tak ,że ilekroć g nie jest tożsamością w G, U ∩ gU jest puste. Właściwe nieciągłe grupy transformacji są przydatne dla studiowania przestrzeni pokrytych, które są dane przez odwzorowanie X → Y tak ,że dowolny punkt w Y ma (spójne) otoczenie U , którego przeciwobraz jest sumą rozłączną zbiorów otwartych X każdy homoemorficzny do U. Określona instancja tegi jest pokryciem przestrzeni homogenicznej przez grupę Lie: inkluzja grup Lie H → G ma przestrzeń warstwy G/H która dziedziczy topologię ilorazową z G; przekształcenie ilorazowe G → G/H jest odwzorowaniem nakrywającym proper subset (of a set) [podzbiór właściwy (zbioru)] : Zbiór S jest właściwym podzbiorem zbioru T jeśli S jest podzbiorem T ale S nie jest równy T. Zatem, zbiór nie jest właściwym podzbiorem samego siebie. Na przykład {3,10} jest właściwym podzbiorem {3,10,47}. Zapis nie jest całkowicie jednostajny. Jeśli S jest właściwym podzbiorem z T, wielu oznacza go przez S ⊂ T propositional calculus [rachunek zdań] : Syntaktyczna część logiki zdaniowej. Rachunek zdań jest systemem formalnym, składającym się z alfabetu, zbioru dobrze ułożonych formuł, określonego zbioru dobrze sformułowanych formuł, które są nazywane aksjomatami , i listy zasad dedukcji. Dobrze ułożone formuły, które są aksjomatami są formułami, które są intuicyjnie oczywiste ,i powinny być tautologiczne. Typowym aksjomatem, który może wystąpić w rachunku zdań będzie propositional logic [logika zdań] : Logika formalna z następującymi symbolami alfabetycznymi pseudozwarta przetsrzeń topologiczna : Przestrzeń topologiczna X z taką właściwością ,że każda ciągła funkcja rzeczywista definiowana w X jest ograniczona. Przestrzeń pseudozwarta odgrywa znaczącą rolę w teorii C*-algebr pseudorozmaitość : Kompleks symplicjalny S , który jest sumą n- sympleksów (dla pewnego n) i spełaniający: pseudopierwsza liczba : 1.Nieparzysta liczba całkowita złożona, n , z taką właściwością ,że 2n ≡ 2 (mod n). To znaczy, n jest liczbą pseudopierwszą jeśli n jest dzielnikiwem 2 pitagorejskie ciało : Ciało, F, w którym suma kwadratów dwóch elementów z tego ciała jest kwadratem elementu tego ciała. To znaczy, F jest pitagorejskie, jeśli , dla każdego a i b w F, istnieje c w F takie ,że a2 + b2 = c2 . Liczby wymierne nie są pitagorejskie ponieważ 12 + 12 = 2 nie jest kwadratem liczby wymiernej. Jednakże, liczby rzeczywiste są ciałem pitagorejskim ponieważ √a2 + b2 jest liczbą rzeczywistą kiedy a i b są rzeczywiste pitagorejski trójkąt : Trójkąt dodatnich liczb całkowitych (a,b,c) spełniających równanie a2 + b2 = c2. Jeśli (a,b,c) jest trójkątem pitagorejskim i a,b i c są względnie pierwsze, wtedy (a,b,c) są znane jako pierwotny trójkąt pitagorejski. Można wykazać ,że albo a albo b (albo obie) muszą być parzyste jeśli (a,b,c) jest trójkątem pitagorejskim. Faktycznie , (a,b,c) jest trójkątem pitagorejskim jeśli i tylko jeśli istnieją liczby całkowite dodatnie k,m i n takie ,że gcd(m,n) = 1 , dokładnie jedna z m lub n jest parzysta, a = (m2 - n2)k, b = 2mnk a c= (m2 + n2)k, dostarczając formuły dla wygenerowania wszystkich trójkątów pitagorejskich
f0, f1, …, fk = f
funkcji takich ,zed la wszystkich i,0 ≤ i ≤ k
(i)fi jest funkcją początkową
(ii) fi może być uzyskana z { fj : 0 ≤ j < i} przez złożenie lub rekurencję
Poniższe funkcje są funkcjami początkowymi:
• S(x) = x + 1 (funkcja następnika)
• Cin(x1, … , xn) = 1, dla wszystkich liczb naturalnych i, n ≥ 0 (funkcje stałe
• Pin(x1, … , xn), dla wszystkich liczb naturalnych n ≥ 1 i 1 ≤ i ≤ n (funkcje rzutowe)
Niech g1, …, gk, f , będą n-arnymi funkcjami i niech h będzie k-arną funkcją; niech x^ oznacza n-krotkę x1, … xn. Funkcja f jest uzyskiwana z g1, …, gk ah przez złożenie jeśli dla wszystkich liczb naturalnych x1, …, xn, f(x^) = h(g1(x^), …, gk(x^)). Niech f będzie n-arną funkcją, n ≥ 1, g będzie (n-1)-arną funkcją, h będzie (n+1)-arną funkcją, a y^ oznacza (n-1)-krotkę y1, …, yn-1. Funkcja f jest uzyskiwana z g i h przez rekurencję jeśli dla wszystkich liczb naturalnych x,y1, …, yn-1
f(0,y^) = g(y^)
f(x+1),y^) = h(x,f(x,y^),y^)
Na przykład, funkcja f(x,y) = x + y jest pierwotnie rekurencyjna. Nieformanie, równania rekurencji dla f to
f(0,y) = y
f(x+1,y) = S(f(x,y))
Bardziej formalnie
f(0,y) = P11(y)
, … , xn, … (n ∈ N) elementów w S ,taki ,że (xn, xn+1) ∈ R dla wszystkich n ∈ N. Ta zasada jest również znana jako Aksjomat Wyboru Zależnego. Jest słabszy niż Aksjomat Wyboru, i zwykle jest zastępowany Aksjomatem Wyboru jeśli założono Aksjomat Określoności
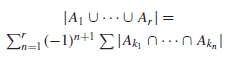
gdzie druki zakres sumy nad wszystkimi n-krotkami liczb naturalnych (k1,… , kn) takich ,że 1 ≤ k1 < … < kn ≤ r
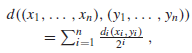
gdzie di jest metyrką na Xi a (x1, … xn), (y1, … yn) ∈ x1 x … x Xn. Ta definicja pokazuje ,że skończony iloczyn przestrzeni metryzowalnych jest metryzowalny
∏n1 = {A ⊆ X:X \ A ∈ ∑n1}
a wtedy niech ∑n+11 będzie zbiorem wszystkich rzutów ∏n1 zbiorów w X x NN, gdzie NN jest przestrzenią Baire′a. Niech Δn1 = ∑n1 ∩ ∏n1, wtedy zbiory w
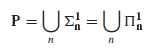
są zbiorami rzutowymi. Formują one hierarchię ponieważ dla każdego n ≥ 1
∑n1 ∪ ∏n1 ⊆ Δnn+1 = ∑nn+1 ∩ ∏nn+1
Dodatkowo
Δ11 = Borel
Klasy rzutowe ∑n1,∏n1 i Δn1 są również znane jako klasy punktu Lusina
(i)αi ∈ Λ (tzn. αi jest aksjomatem logicznym
albo
(ii)Istnieje 1 ≤ j1 < … < jk < i takie ,że αij1
Formuła α jest udowadnialna z rachunku predykatów (zapis : |- α) jeśli istnieje dowód z α z rachunku predykatów. Jeśli Γ jest zbiorem dobrze ułożonych formułz L, wtedy dowód α z Γ jest ciagiem α1,α2, … , αn dobrze ułożonych formuł z L, taki ,że αn = α i taki ,że dla wszystkich i, 1 ≤ i ≤ n, albo
(i)αi ∈ Γ ∪ Λ
albo
(ii)Istnieje 1 ≤ j1 < … < jk < i takie ,że αi może być wydedukowany z αj1, … , αjk, używając zasady interferencji. Formuła α jest udowadnialna z Γ w rachnku predykatów (zapis : |- α) jeśli istnieje dowód α z Γ w rachunku predykatów. Zapis dowodu w logice zdaniowej jest całkowicie analogiczna. Zapis dowodu w logice formalne jest również nazywana dowodem formalnym lub dedukcją
(&alpga; → (β → α))
gdzie α i β są dobrze ułożonymi formułami zdaniowymi (to znaczy w rzeczywistości nazywane schematem aksjomatu, niż aksjomatem, ponieważ jest nieskończenie wiele aksjomatów tej postaci, po jednym dla każdego różnego wyboruz α i β. Typowa zasada dedukcji w rachunku zdań to modus ponens. Rachunek zdań , używając aksjomatów i zasad dedukcji, jest używany do udowadniania twierdzeń. Ponieważ wybór aksjomatów i zasad dedukcji nie jest ważny, ważne jest że rachunek zdań jest logiczny (tzn. dobrze ułożone formuły , które są udowadniane z systemu formalnego powinny być tautologią) i kompletny (tzn. tautologia powinna być udowadniana z systemu formalnego)
(i)( , ) (nawisay okrągłe)
(ii)¬ , ∧ , ∨ , → , ↔ (spójniki logiczne)
(iii)A1,A2,A3, … (symbole nielogiczne)
Często lista logicznych spójników w pozycji (ii) jest skrócona do kompletnej listy logicznych spójników, takich jak {¬ , →} .Symbol An jest nazywany n-tym symbolem zdaniowym.. Symbole zdaniowe nie mają znaczenia , chociaż używają prawdziwych przypisani, które mogą być interpretowane jako prawda albo fałsz. Logika zdaniowa ma zasady, które mówią jakie wyrażenia z języka są dobrze ułożonymi formułami. Rachunek zdań jest używany do tworzenia twierdzeń logiki zdaniowej. Prawdziwe przypisanie prowadzi do zpisu semantycznego prawdy w logice zdaniowej, podczas gdy rachuenk zdań podaje syntaktyczny zapis dowodzenia
(i)każda n-1-sympleks z S jest ścianką dokładnie dwóch n-sympleksów