Latin square [kwadrat łaciński] : Tablica n x n liczb takich ,że każdy wiersz i kolumna tablicy zawierają te same liczby a każda liczba pojawia się dokładnie raz w każdym wierszu i kolumnie. Na przykład

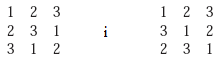
lattice [krata, sieć, struktura] : Nie pusty zbiór X, razem z dwoma działaniami binarnymi ∪ , ∩ na X (nazywane odpowiednio, sumą i częścią wspólną), która spełnia poniższe warunki dla wszystkich A,B,C ∈ X:

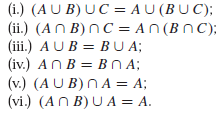
leaf [liść] : Rozmaitość , która jest maksymalna całkową podrozmaitością rozkładu całkowego. Przy danej rozmaitości M, rozkład Δ przypisuje do każdego punktu P w M k-wymiarowej podprzestrzeni przestrzeni stycznej przy P. Jest całkowalna jeśli rozmaitość jest sumą k-wymiarowych zanurzonych podrozmaitości, takich ,że k-płaszczyzna Δ(p) jest płaszczyzną styczną k-rozmaitości przez p. Liść jest maksymalnie spójna całkową podrozmaitością rozkładu

least common multiple [najmniejsza wspólna wielokrotność] : Dla dwóch niezerowych liczb całkowityhc a i b, najmnijesza liczba dodatnia całkowita L taka ,że jest wielokrotnością zarówno a i b, jest oznaczana przez LCM(a,b). Równoważnie, LCM(a,b) jest jednoznaczną liczbą dodatnią całkowitą, która jest wielokrotnością zarówno a i b i jest podzielnikiem wszystkich innych wspólnych wielokrotności a i b. Na przykład, LCM(14,8) = 56 a LCM(3,5) = 15. Zwróć uwagę ,że najmniejsza wspólna wielokrotność dwóch liczb całkowitych niezerowych zawsze będzie dzielnikiem iloczynu tych dwóch liczb całkowitych. Faktycznie, iloczyn największego wspólnego dzielnika i najmniejszego wspólnego dzielnika dwóch liczb całkowitych jest iloczynem tych dwóch liczb całkowitych. (tj. ab = gcd(a,b) ⋅ LCM(a,b))

least element [element najmniejszy] : Przy danym zbiorze A z porządkiem &le na A, elelemnt l ∈ A będącym najmniejszym elementem z A , jeśli , dla wszystkich x ∈ A, l ≤ x. Zauważ ,że jeśli A ma najmniejszy element, wtedy jest jednoznaczny.

least upper boud [kres górny, supremum] : Niech A będzie zbiorem uporząkowanym i niech B ⊆ A. Element u &isisn; A będący kresem górnym dla B jeśli jest górna granica dla B (tj .dla wszystkich x ∈ B , x ≤ u) i jest najmniejszy element w tym zbiorze wszystkich górnych granic dla B (tj. dla wszystkich y ∈ A, jeśli dla wszystkich x ∈ B, x ≤ y, wtedy u ≤ y). Zwróć uwagę ,że jeśli zbiór ma kresem górnym , wtedy jest jednoznaczny.

lewo sprzężony funktor : Niech C i D będą kategoriami z funktorami F:C → D i G: D → C takie ,że jeśli X jest obiektem C a Y jest obiektem D, mamy bijekcję
hom_C(X,G(Y)) = hom_D(F(X),Y)
który jest naturalnym w X i Y. Wtedy F jest lewo sprzężone dla G a G jest prawo sprzężony do F.

leg [przyprostokątna] : Trójkącie prostokątnym, jedna z dwóch boków przy kącie prostym.

level (of a tree) [poziom drzewa] : α-ty poziom drzewa T, Lev_α(T), jest zbiorem wszystkich elementów z T których poprzednicy mają rząd typu α. To znaczy, dla dowolnego t ∈ T, zbiór poprzedników t , {s ∈ T : s < t}, musi być dobrze uporządkowany, a poziom t jest podany przez ich typ porządkowy. Lev₀(T) jest zbiorem elementów w T bez poprzedników, podczas gdy Lev₁(T) jest zbiorem elementów z dokładnie jednym poprzednikiem (który musi pochodzić z poziomu 0)

Lie grupa : Grupa , która jest również różniczkowalną rozmaitością i dla której iloczyn i przekształcenie odwrotne są nieskończenie różniczkowalne ( i dlatego jest grupą topologiczną)

Lie przekształcenie linia-kula : Odpowiedniość między liniami w przestrzeni R, I kulami w odpowiedniej przestrzeni S, nazwanej po norweskim matematyku Mariusie Sophusie Lie. Punkt (X,Y,Z) ∈ S określa lnię w R przez dwa równania:

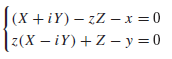
Dla dowolnej stałej linii w R, zbiór takich linii , które napotykają l odpowiednie do sfery w S (której środek i/lub promień mogą być liczbami zespolonymi).

limit cardinal [graniczna liczba kardynalna} Liczba kardynalna ℵ_α, której indeks &aplpha; jest graniczną liczbą porządkową

limit ordinal [granicznna liczba porządkowa] : Liczba porządkowa α która nie jest następnikiem liczby porządkowej. Dlatego też, α ma postać sup{β : β < α} = ∪_{β < α}β (Należy zaznaczy ,że 0 jest również graniczną liczbą porządkową; określamy sup∅ = 0)

line bundle [wiązka liniowa] : Termin używany w teorii wiązek wektorowych. Wiązka wektorowa nad przestrzenią topologiczną X składa się z przestrzeni E nazwanej przestrzenią całkowitą, przestrzeń wektorowa F nazwana włóknem i przekształcenia π : E → X. Przestrzeń X ma pokrycie prze zbiory otwarte U_i z homeomorfizmem Φ_i z E_i = π^-1(U_i do U_i x F. Przekształcenie rzutowe π przestrzega te struktury iloczynu tj. πoΦ_i^-1(x,V) = x . Kiedy x ∈ U_i ∩ U_j, przekształcenie g_ij(x) : F → F definiowane przez (x,g_ij(x)(V)) = Φ_j(Φ_i^-1(x,V)) jest wymagane aby być liniowym. Implikuje to ,że π^-1(x) ma strukturę przestrzeni wektorowej. Wiązka liniowa jest wiązką wektorową z jednowymiarowym włóknem. Zazwyczaj pole jest albo liczbami rzeczywistymi lub liczbami zespolonymi.

line of curvature [linia krzywizny] : Krzywa C na powierzchni, mająca właściwość ,że każdy punkt C(t) jest na krzywej ,wektor styczny C′(t) jes głównym wektorem na powierzchni przy C(t), to znaczy wektor włąsny przekształcenia Weingartena

line segment [odcinek prostej] : Wszystkie punkty P na lini określonej przez dwa dane punkty A I B leżące między A i B na płaszczyźnie .Dla takiego punku P, punkty A i B leżą na różnych półprostych z P. Definicja ta ma sens w geometrii płaszczyzny hiperbolicznej ale nie geometrii eliptycznej, gdzie gdzieś pomiędzy nie jest dobrze sformułowaną koncepcją.

liniowa funkcja ułamkowa : Bijekcja rozszerzonej płaszczyzny zespolonej C ∪ {∞} zdefiniowana przez z |-> az+b/cz+d dla danych liczb zespolonych a,b,c,d takich ,że ad-bc ≠ 0. Odwrotność jest dana przez z |-> dz-b/cz-a. Nazywana również przekształceniem Möbiusa, homografia, liniową transformacją.

liniowo uporzadkowany zbiór : Zbiór A z liniowym porządkiem na A

liniowy porządek : Częściowe uporządkowanie ≤ na zbiorze A w której każda para różnych elementów A jest porównywalna; tj. dla wszystkich x,y ∈ A, jeśli x ≠ y , wtedy x ≤ y lub y ≤ x. Jeśli uporządkowanie częściowe jest typu < , wtedy < jest porządkiem liniowym, jeśli dla wszystkich x,y ∈ A, jeśli x ≠ y, wtedy x < y lub y , x. Zwykły porządek ≤ na Q, zbiór liczb wymiernych, jest liniowo uporządkowany

link : 3 jest podzbiorem R³ który jest homeomorficzny do n różnych kopii S¹. Pojedyncze komponenty mogą być wiązane ze sobą lub z innymi komponentami. Bardziej ogólnie, wiązanie n komponentów w R^m+2 jest m osadzoną skończoną liczbą kopii S^m w R^m+2 lub S^m+2. Dwa wiązania L₁, L₂ są równoważne jeśli jest homomorfizmem h:R^m+2 → R^m+2 (lub h:S^m+2 → S1) = L₂

Liouville′a funkcja : Funkcja arytmetyczna , oznaczona λ, która dla dowolnej liczby dodatniej całkowitej n = p₁^i₁ ... p_k^i_k
, zwracająca liczbę λ(n) = (-1)^{i₁ + ... + i_k}. Jest całkowicie multilikatywna

lokalnie n-spójna przestrzeń topologiczna Przestrzeń topologiczna taka ,że , dla kążdego punktu p, każde sąsiedztwo p zawierające najmniejsze sąsiedztwo p które jest n-spójne. Spójna przestrzeń topologiczna X jest n-spójna jeśli dla każdego k ≤ n , każde przekształcenie k-wymiarowej sfery do X jest homotopiczne do stałego przekształcenia. Na przykład, dowolna rozmaitość jest lokalnie n-spójna dla każdego n , ponieważ jest lokalnym skończonym kompleksem symplicjalnym. Jeden punkt sumy nieskończenie wielu n-sfer , ze słabą topologią, jest lokalnie n-1 spójny a nie lokalnie n-spójny

logiczne spójniki : Używane do budowania nowych zdań lub formuł pierwszego rzędu z istniejących. Zwykle spójniki logiczne to ∧ (i), ∨ (lub) , ¬ (nie), → (implikacja) i ↔ (jeśli i tylko jeśli).

logiczna konsekwencja : w logice zdaniowej, poprawnie zbudowana β jest logiczną konsekwencją poprawnie zbudowanej α jeśli α logicznie implikuje β , tj. jeśli każde prawdziwe zdanie, które spełnia α również spełnia β. Na przykład jeśli A i B są symbolami zdania, wtedy A jest logiczną konsekwencja (A ∧ B). Dodatkowo β jest logiczną konsekwencją zbioru Γ poprawnie zbudowanego jeśli Γ logicznie implikuje β, tj. jeśli każde prawdziwe zdanie, które spełnia każdy element Γ również spełnia β .Dla logiki pierwszego rzędu, niech L będzie językiem pierwszego rzędu i niech α i β będą poprawnie zbudowane z L. Wtedy β jest logiczną konsekwencją z α jeśli α logicznie implikuje β tj. jeśli, dla każdej struktury A dla L i dla każdego s : V → A, kiedy A spełnia α z s, A również spełnia β z s. (Tu V jest zbiorem zmiennych L i A jest populacją generalną z A). Dodatkowo, β jest logiczną konsekwencją zbioru Γ poprawnie zbudowaną z L jeśli Γ logicznie implikuje β tj. jeśli dla każdej struktury A dla L i dla każdego s : V → A, kiedy A spełnia każdą składową z Γ z s, A również spełnia β

logiczny równoważnik : W logice zdaniowej, poprawnie zbudowane α i β są logicznie równoważne jeśli α logicznie implikuje β a β logicznie implikuje α; to znaczy jeśli każde prawdziwe zdanie albo spełnia zarówno α i β lub zarówno ¬α i ¬β. Na przykład, jeśli A i B są symbolami zdań , wtedy (¬(A ∨ B)) i ((¬A) ∧ (¬B)) są logicznie równoważne. Dla logiki pierwszego rzędu, niech L będzie językiem pierwszego rzędu i niech α i β będą poprawnie zbudowanymi z L. Wtedy α i β są logicznie równoważne jeśli α logicznie implikuje β a β logicznie implikuje α tzn. jeśli dla każdej struktury A dla L i dla każdego s : V → A , A spełnia α z s jeśli i tylko jeśli A spełnia β z s. (Tu ,V jest zbiorem zmiennych z L a A jest populacją generalną z A)

logiczna implikacja : W logice zdaniowej, poprawnie zbudowana α logicznie implikuje inną poprawnie zbudowaną β (notacja : α |= β) jeśli każde prawdziwe zdanie , które spełnia α spełnia też β. Zbiór Γ poprawnie zbudowany logicznie implikuje poprawnie zbudowane β (notacja : Γ |= β) jeśli każde prawdziwe zdanie które spełnia element z Γ również spełnia β. Na przykład, jeśli A,B i C są symbolami zdań , Γ = {A,(A → B)}, a β = B, wtedy Γ logicznie implikuje β. Dla logiki pierwszego rzędu, niech L będzie językiem pierwszego rzędu i niech α i β będą poprawnie zbudowne z L. Wtedy α logicznie implikuje β (notacja : α |= β) jeśli dla każdej struktury A dla L i dla każdego s: V → A takiego ,że A spełnia α z s, A również spełnia β z s (Tu, V jest zbiorem zmiennych z L i A jest populacją generalną z A) Zbiór Γ poprawnie zbudowany z L logicznie implikuje poprawnie zbudowany β z L (notacja: Γ |= β) jeśli dla każdej struktury A dla L i dla każdego s : V → A takiego ,że A spełnia każdą składową Γ z s, A również spełnia β z s.

Loop Theorem [Twierdzenie Pętli] : Twierdzenie zajmujące się warunkami w jakich pętla na granicy trójwymiarowej rozmaitości która jest ściągalna wewnątrz rozmaitości ma równoważne osadzenie z granicą dysku. Szczególnie, niech M będzie zwartą trzywymiarową rozmaitością i niech N będzie składową jej granicy .Jeśli jądro homomorfizmu π₁(N) → π₁(M) nie jest trywialne, wtedy istnieje dysk D² ⊂ M taki ,że ∂D^<2 ⊂ N jest prostą pętlą która nie jest homotopizna do zera w M.

lower bound [ograniczenie dolne] : Niech S będzie podzbiorem częściowo uporządkowanej zbioru (P,≤). Element x ∈ P jest ograniczeniem dolnym dla S , jeśli x ≤ s dla wszystkich s ∈ S

Łuzina przestrzeń : Nieprzeliczalna regularna przestrzeń topologiczna, która nie ma punktów izolowanych i w której każdy zbiór nigdziegęsty jest policzalny.